前言
图的遍历算法是求解图的连通性问题、拓扑排序和求关键路径等算法的基础。
通常有两种遍历图的方式:广度优先和深度优先(有无向图和有向图都适用),下面以有向图为例给出基于python的两种实现。
已知图如下所示:
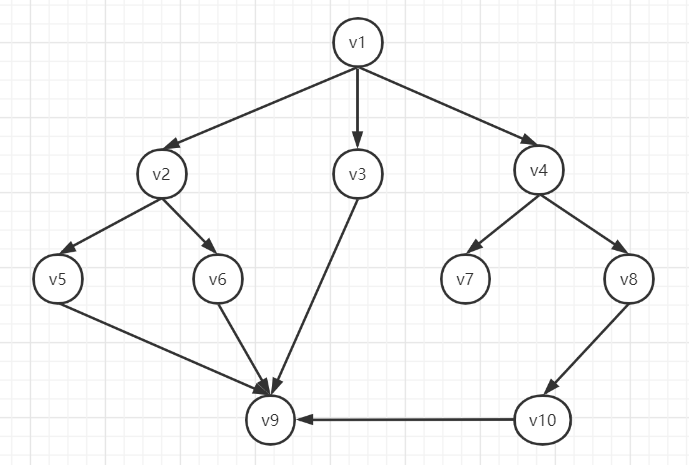
广度优先搜索
from collections import deque
VISITED = []
# breadth first search
def bfs(d):
VISITED.append("v1")
q = deque()
q += d["v1"]
while q:
item = q.popleft() # first in first out
if item not in VISITED:
VISITED.append(item)
q += d[item]
if __name__ == "__main__":
d = {}
d["v1"] = ["v2", "v3", "v4"]
d["v2"] = ["v5", "v6"]
d["v3"] = ["v9"]
d["v4"] = ["v7", "v8"]
d["v5"] = ["v9"]
d["v6"] = ["v9"]
d["v7"] = []
d["v8"] = ["v10"]
d["v9"] = []
d["v10"] = ["v9"]
bfs(d)
print(VISITED)
# ['v1', 'v2', 'v3', 'v4', 'v5', 'v6', 'v9', 'v7', 'v8', 'v10']
深度优先搜索
深度优先搜索存在一个回溯的过程,所以使用递归来实现,因为递归本身保存了调用栈。
VISITED = []
def recurse(items, d):
if not items:
return None
for item in items:
if item not in VISITED:
VISITED.append(item)
recurse(d[item], d)
# depth first search
def dfs(d):
VISITED.append("v1")
recurse(d["v1"], d)
if __name__ == "__main__":
d = {}
d["v1"] = ["v2", "v3", "v4"]
d["v2"] = ["v5", "v6"]
d["v3"] = ["v9"]
d["v4"] = ["v7", "v8"]
d["v5"] = ["v9"]
d["v6"] = ["v9"]
d["v7"] = []
d["v8"] = ["v10"]
d["v9"] = []
d["v10"] = ["v9"]
dfs(d)
print(VISITED)
# ['v1', 'v2', 'v5', 'v9', 'v6', 'v3', 'v4', 'v7', 'v8', 'v10']