M斐波那契数列
F[0] = a
F[1] = b
F[n] = F[n-1] * F[n-2] ( n > 1 )
现在给出a, b, n,你能求出F[n]的值吗?
Input
输入包含多组测试数据;
每组数据占一行,包含3个整数a, b, n( 0 <= a, b, n <= 10^9 )Output对每组测试数据请输出一个整数F[n],由于F[n]可能很大,你只需输出F[n]对1000000007取模后的值即可,每组数据输出一行。
Sample Input
0 1 0 6 10 2
Sample Output
0 60
解题思路:
本题有多组测试,给定公式F[n] = F[n-1] * F[n-2] ( n > 1 ) ,每组测试给出三个整数a,b,n,a与b分别为第一位与第二位的值,n为需要求出的位。
我们根据给出的公式继续向下寻找规律
F[0] = a F[1] = b F[2] = a * b F[3] = a * b * b = a * b^2 F[4] = a * b^2 * a * b = a ^2 * b ^3 F[5] = a ^2 * b^3 * a * b^2 = a^3 * b^5 F[6] = a^3 * b^5 * a^2 * b^3 = a^5 * b^8 F[7] = a^5 * b^8 * a^3 * b^5 = a^8 * b^13 F[8] = a^8 * b^13 * a^5 * b^8 = a^13 * b^21 …… 再观察一手斐波那契数列f(n) 1、1、2、3、5、8、13、21…… 哦,天哪!!! F[n] = a^f(n-1) * b^f(n) ( n > 1 ) 找到了规律!获得了巨大的快乐
这个题已经简化为了求a的斐波那契数列n-1项次幂 * b的斐波那契数列n项次幂。
斐波那契数列第n项和n-1项怎么求,递归?——不行,n < 1e9 太庞大。
斐波那契数列公式f(n) = f(n - 1) + f(n - 2),我们拿出相邻的两项建立一个2 * 1的矩阵
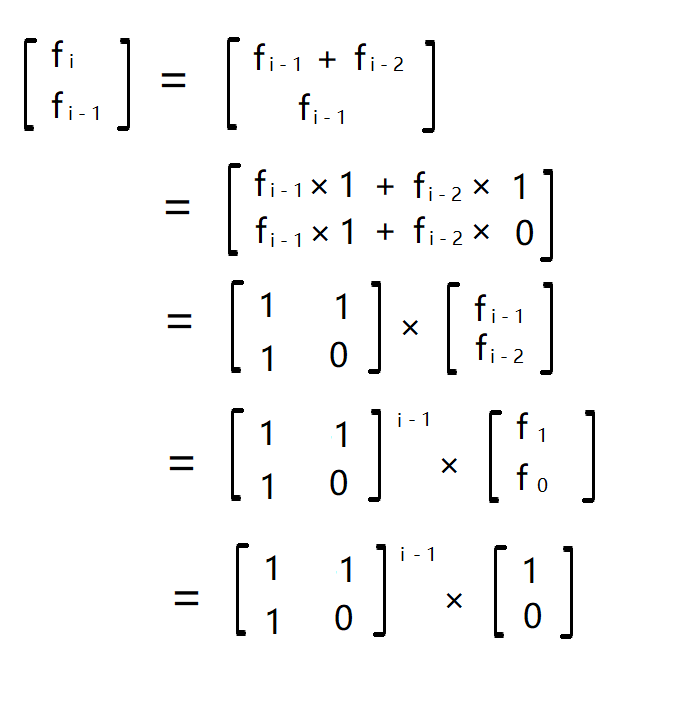
想要求斐波那契数列的第n项与第n-1项只需求出初始矩阵的n-1次幂即可,之后求出a的第n-1项次幂与b的第n项次幂即可。
这里就要用到快速幂,与矩阵快速幂。
快速幂思想:求2^11,11的二进制位1011,11 = 1*2^3 + 0*2^2 + 1*2^1 + 1*2^0,所以可以将2^11转化为2^(2^0) * 2^(2^1) * 2(2^3)。将原先的11次 O(n)优化为了3次O(logn),本题要求取模,又因为积的取余等于取余的积的取余,我们可以直接在快速幂的过程中取模以得到取模后的答案。
快速幂取模:

LL power(int a, int b, int mod){ //快速幂 LL ans = 1; while(b){ if(b & 1){ //从b的二进制末位开始判断 ans = ans * a % mod; //如果为1更新取模后的答案 } a = a * a % mod; //更新底数取模 b >>= 1; //b右移一位 } return ans; }
矩阵快速幂与快速幂思想基本一直,只是传入的底数变为了矩阵,乘法也变成了矩阵相乘,这时我们只要开一个结构体记录矩阵并重载*运算符为矩阵乘法即可,根据矩阵乘法运算规则,对于新的*运算我们只要两层for循环,依次计算答案矩阵,之后再内部一层for循环让第一个矩阵只移动行第二个矩阵只移动列,对应相乘再求和即可得出答案。

struct matrix{ LL mat[maxn][maxn]; //mat记录当前矩阵 matrix operator *(const matrix &a)const{ //重载运算符* matrix ans; for(int i = 0; i < 2; i++){ //遍历行 for(int j = 0; j < 2; j++){ //遍历列 ans.mat[i][j] = 0; //初始化答案矩阵该位置为0 for(int k =0; k < 2; k++){ //第一个矩阵第i行与第二个矩阵第j列对应相乘 ans.mat[i][j] = (ans.mat[i][j] + mat[i][k] * a.mat[k][j]) % (mod-1); } } } return ans; //返回答案矩阵 } }; matrix power(matrix a, LL b){ //矩阵快速幂 matrix ans; //答案矩阵 memset(ans.mat, 0, sizeof(ans.mat)); //初始答案矩阵为单位矩阵 for(int i = 0; i < 2; i++){ ans.mat[i][i] = 1; } while(b){ if(b & 1){ ans = ans * a; } b >>= 1; a = a * a; } return ans; }
AC代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 const LL mod = 1e9+7; 5 const int maxn = 2; 6 struct matrix{ 7 LL mat[maxn][maxn]; //mat记录当前矩阵 8 matrix operator *(const matrix &a)const{ //重载运算符* 9 matrix ans; 10 for(int i = 0; i < 2; i++){ //遍历行 11 for(int j = 0; j < 2; j++){ //遍历列 12 ans.mat[i][j] = 0; //初始化答案矩阵该位置为0 13 for(int k =0; k < 2; k++){ 14 //第一个矩阵第i行与第二个矩阵第j列对应相乘 15 ans.mat[i][j] = (ans.mat[i][j] + mat[i][k] * a.mat[k][j]) % (mod-1); 16 } 17 } 18 } 19 return ans; //返回答案矩阵 20 } 21 }; 22 matrix power(matrix a, LL b){ //矩阵快速幂 23 matrix ans; //答案矩阵 24 memset(ans.mat, 0, sizeof(ans.mat)); //初始答案矩阵为单位矩阵 25 for(int i = 0; i < 2; i++){ 26 ans.mat[i][i] = 1; 27 } 28 while(b){ 29 if(b & 1){ 30 ans = ans * a; 31 } 32 b >>= 1; 33 a = a * a; 34 } 35 return ans; 36 } 37 LL pownum(LL a, LL b){ 38 LL ans = 1; 39 while(b){ 40 if(b & 1){ 41 ans = ans * a % mod; 42 } 43 b >>= 1; 44 a = a * a % mod; 45 } 46 return ans; 47 } 48 int main() 49 { 50 LL a ,b, n; 51 52 while(scanf("%lld%lld", &a, &b) != EOF){ //输入a与b的值 53 matrix a; 54 scanf("%lld", &n); //输入n 55 a.mat[0][0] = 1; 56 a.mat[0][1] = 1; 57 a.mat[1][0] = 1; 58 a.mat[1][1] = 0; 59 //初始矩阵 60 //特判0与1 61 if(n == 0){ 62 printf("%lld ", a); 63 }else if(n == 1){ 64 printf("%lld ", b); 65 }else{ 66 a = power(a, n - 1); //矩阵快速幂计算斐波那契数列第n-1项与第n项 67 LL ta = a.mat[0][1]; //第n-1项 68 LL tb = a.mat[0][0]; //第n项 69 LL ans = (pownum(a, ta) * pownum(b, tb)) % mod; 70 //计算答案 71 printf("%lld ", ans); 72 } 73 } 74 return 0; 75 }
