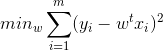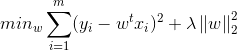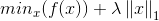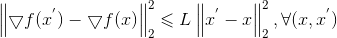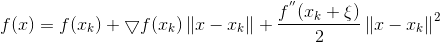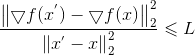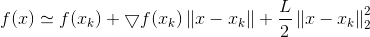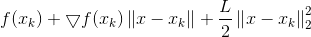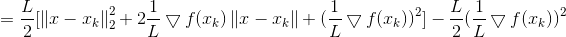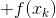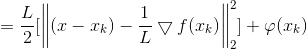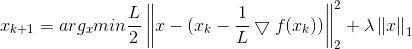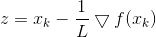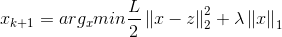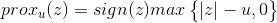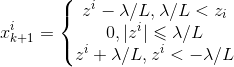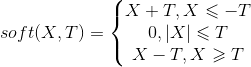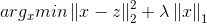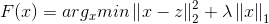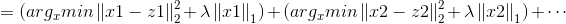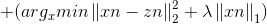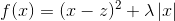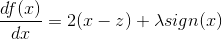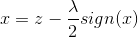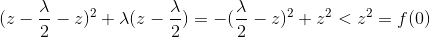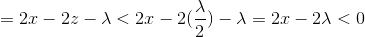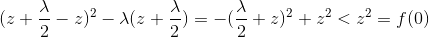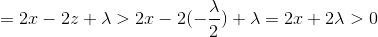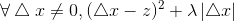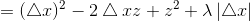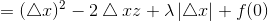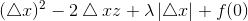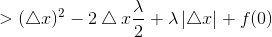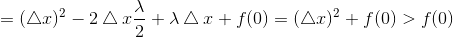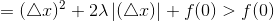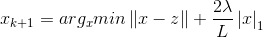LASSO回归与L1正则化 西瓜书
1.结构风险与经验风险
在支持向量机部分,我们接触到松弛变量,正则化因子以及最优化函数,在朴素贝叶斯分类,决策树我们也遇到类似的函数优化问题。其实这就是结构风险和经验风险两种模型选择策略,经验风险负责最小化误差,使得模型尽可能的拟合数据,而结构风险则负责规则化参数,使得参数的形式尽量简洁,从而达到防止过拟合的作用.所以针对常见模型,我们都有下式:
第一项经验风险L(yi,f(xi,w))衡量真实值与预测值之间的误差,第二项结构风险Ω(w)规则化项使得模型尽可能简单.而第二项Ω(w)一般是模型复杂度的单调函数,模型越复杂,则规则化项的值越大,这里常引入范数作为规则化项,这也就引入了我们常见的L0范数,L1范数以及L2范数.
2.L0范数,L1范数,L2范数与LASSO回归,岭回归
1)广义定义
L0范数 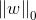
L1范数 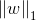
L2范数 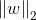
L0,L1范数可以实现稀疏化,而L1系数因为有比L0更好的特性而被广泛应用,L2范数在回归里就是岭回归,也叫均值衰减,常用于解决过拟合,通过对向量各元素平方和再求平方根,使得L2范数最小,从而使得参数W的各个元素都接近于0,与L1范数不同,L2范数规划后w的值会接近于0但不到0,而L1范数规范后则可能令w的一些值为0,所以L1范数规范在特征选择中经常用到,而L2范数在参数规则化时经常用到.在回归模型中,通过添加L1,L2范数引入正则化项,便得到了LASSO回归和岭回归:
2)回归模型
常见线性模型回归:
LASSOO回归:
岭回归:
3.嵌入式选择与LASSO回归
这里主要针对西瓜书第11节的内容,对近端梯度下降PGD法解决L1正则化问题进行讨论.
1)优化目标
令▽表示微分算子,对优化目标:
若f(x)可导,且▽f 满足L-Lipschitz(利普希茨连续条件),即存在常数L>0使得:
2)泰勒展开
则在Xk处我们可以泰勒展开:
上式是严格相等,由L-Lipschitz条件我们可以看到:
这里给出了一个L的下界,且下界的形式与二阶导函数形式类似,从而泰勒展开式的二阶导便通过L替代,从而严格不等也变成了近似:
3)简化泰勒展开式
接下来我们化简上式:
其中φ(xk)是与x无关的const常数.
4)简化优化问题
这里若通过梯度下降法对f(x)进行最小化,则每一步下降迭代实际上等价于最小化二次函数f(x),从而推广到我们最上面的优化目标,类似的可以得到每一步的迭代公式:
令
则我们可以先计算z,再求解优化问题:
5)求解
令xi为x的第i个分量,将上式展开可以看到没有xixj(x≠j)的项,即x的各分量互不影响,所以优化目标有闭式解.这里对于上述优化问题求解需要用到Soft Thresholding软阈值函数,其解为:
对于本例,带入求解即得:
因此,PGD能使LASSO和其他基于L1范数最小化的方法得以快速求解.
4.Soft Thresholding软阈值函数证明
1)软阈值函数
上式求解用到了软阈值函数,下面对软阈值函数的解进行求证,从而更好理解上述求解过程.
先看一下软阈值函数:
2)证明
Proof:
对于优化问题:
此处X,Z均为n维向量.
展开目标函数:
从而优化问题变为求解N个独立的函数:
这是我们常见的二次函数,对其求导:
令导数为0:
看到两边都有x,所以我们要对上述情况进行讨论:
A.z>λ/2时
假设 x<0 , 所以 sign(x)=-1 ,但 z-λ/2sign(x)>0 ,所以矛盾.
假设 x>0 ,所以 sign(x) = 1,z-λ/2sign(x)>0,所以极小值在x>0 取得1.
此时极小值小于f(0):
再看x<0,
所以f(x)在负无穷到0单调递减,所以最小值在z-λ/2处取得.
B.z<-λ/2时
假设 x<0 , 所以 sign(x)=-1 ,z-λ/2sign(x)<0 ,所以极值点在 x<0 处取得.
假设 x>0 ,所以 sign(x) = 1,z-λ/2sign(x)<0,所以矛盾.
此时极值小于f(0):
再看 x>0 ,
所以f(x)在0到正无穷单调递增,所以最小值在z+λ/2处取得.
C.λ/2<z<λ/2时
假设 x<0 , 所以 sign(x)=-1 ,z-λ/2sign(x)>0 ,所以矛盾.
假设 x>0 ,所以 sign(x) = 1,z-λ/2sign(x)<0,所以矛盾.
所以x>0,x<0均不满足条件.
所以有:
当△x>0时,由条件z<λ/2:
当△x<0时,由条件z<λ/2:
所以在0处取极小值,同时也是最小值.
综合以上三种情况:
3)对应西瓜书的L1正则化与LASSO回归
这里的解对应的优化问题是:
而我们PGD优化的问题是:
对上式同乘2/L不影响极值点位置的选取,所以我们的PGD优化问题变成:
带入综合三种情况的到的最终解:
西瓜书上11.14也就得证了~
总结:
终于看完了西瓜书11章特征选择与稀疏学习,发现从头至尾都在提到用LASSO解决问题,所以就结合第六章的正则化和之前的模型评价,对正则化范数以及LASSO重新认识了一下,书中解决LASSO的大致方法就是通过利普希茨连续条件得到L,带入到优化函数中对函数简化变形,简易优化函数,然后通过软阈值函数得到最后的解.LASSO大致就是这些了,有问题欢迎大家交流~