Mysql数据库中的事务介绍以及操作

1.事务简介

(1)在 MySQL 中只有使用了 Innodb 数据库引擎的数据库或表才支持事务。
(2)事务处理可以用来维护数据库的完整性，保证成批的 SQL 语句要么全部执行，要么全部不执行。
(3)事务用来管理 insert,update,delete 语句。

2.事务的四大特性

2.1 原子性

'''
一个事务（transaction）中的所有操作，要么全部完成，要么全部不完成，不会结束在中间某个环节。事务在执行过程中发生错误，
会被回滚（Rollback）到事务开始前的状态，就像这个事务从来没有执行过一样。
'''　

2.2 一致性

'''
在事务开始之前和事务结束以后，数据库的完整性没有被破坏。这表示写入的资料必须完全符合所有的预设规则，
这包含资料的精确度、串联性以及后续数据库可以自发性地完成预定的工作。(比如：A向B转账，不可能A扣了钱，B却没有收到)
'''　

2.3 隔离性

'''
数据库允许多个并发事务同时对其数据进行读写和修改的能力，隔离性可以防止多个事务并发执行时由于交叉执行而导致数据的不一致。
事务隔离分为不同级别，包括读未提交（Read uncommitted）、读提交（read committed）、可重复读（repeatable read）和串行化（Serializable）。
（比如：A正在从一张银行卡里面取钱，在A取钱的过程中，B不能向这张银行卡打钱）
'''　

2.4 持久性

事务处理结束后，对数据的修改就是永久的，即便系统故障也不会丢失。

3 事务的操作　

# 事务的开启
start transaction;

# sql语句  涉及删除 更新 插入 等操作

# 保存节点
savepoint 节点名;

# 回滚
rollback; # 取消全部事务

rollback to 节点名; # 回到某个节点

# 提交 
commit; 

# 需要注意的是  操作默认是提交的  如果是提交之后 在用rollack则是没有效果的  需要重新更新或者删除等

4 事务操作案例

1 有表如下

2 开启事务 保存节点

start transaction;

insert into class (name,number) values ('五班',50);
savepoint a1;

insert into class (name,number) values ('六班',60);
savepoint a2;

3 查询表

select * from class;

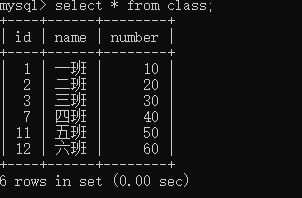
此时有五班六班的信息

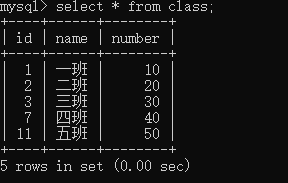
4 执行回滚节点 在查询

rollback to a1;

select * from class; # 没有六班信息 有五班信息

　

5 全部回滚 在查看

rollback;
select * from class;

　　

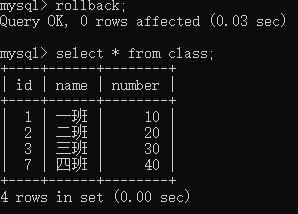
回到原始数据.

但是如果用到commit 则不一样了 

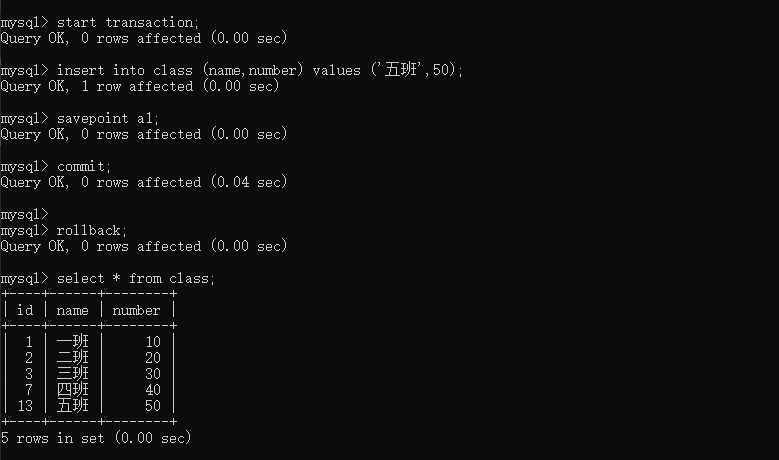
start transaction;
insert into class (name,number) values ('五班',50);
savepoint a1;
commit;

rollback; # commit之后回滚没有效果 

select * from class;  # 五班信息已经保存了