利用sklearn.dataset随机产生数据,随机生成两类数据,用不同的颜色展示出来,如下图:

产生的随机代码如下:
#随机产生的数据 np.random.seed(0) X,y=datasets.make_moons(300,noise=0.25) plt.scatter(X[:,0],X[:,1],s=50,c=y,cmap=plt.cm.Vega20c,edgecolors="Black") plt.title('Random data') plt.show()
一、线性分类
先使用sklearn自带的线性分类方法,将上面的数据分为两类,代码和效果图如下:
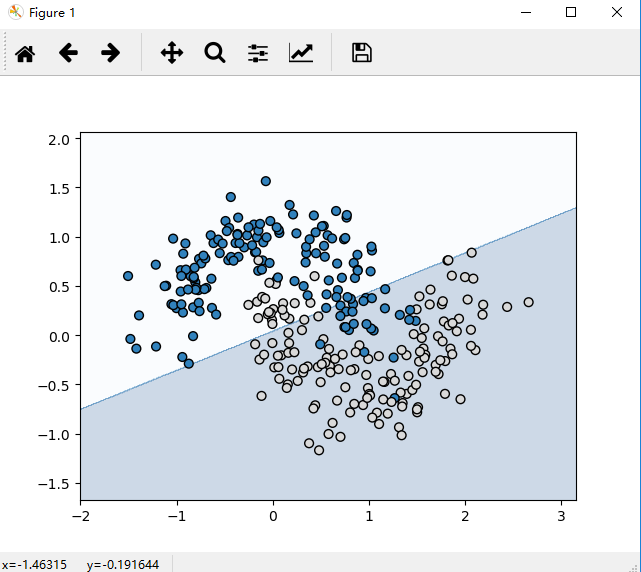
from sklearn import linear_model from sklearn import datasets import sklearn import numpy as np import matplotlib.pyplot as plt #绘制分类边界函数 def plot_boundary(pred_func,data,labels): x_min,x_max=data[:,0].min()-0.5,data[:,0].max()+0.5 y_min,y_max=data[:,1].min()-0.5,data[:,1].max()+0.5 h=0.01 xx,yy=np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h)) z=pred_func(np.c_[xx.ravel(),yy.ravel()]) z=z.reshape(xx.shape) plt.contourf(xx,yy,z,cmap=plt.cm.Blues,alpha=0.2) plt.scatter(data[:,0],data[:,1],s=40,c=labels,cmap=plt.cm.Vega20c,edgecolors="Black") plt.show() #线性分类 logistic_fun=sklearn.linear_model.LogisticRegressionCV() clf=logistic_fun.fit(X,y) #展示分类图 plot_boundary(lambda x:clf.predict(x),X,y) plt.title("Logistic Regression")
二、神经网络分类
定义如下图所示的神经网络:

网络结构:输入层、隐藏层、输出层【2,3,2】
激活函数使用Tanh函数,最后通过Softmax层把激活函数的输出转换为概率
对于分类问题,损失函数使用交叉熵损失,公式如下:
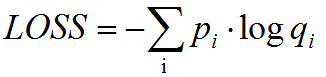
其中,p为期望概率分布(实际值),q为网络输出(预测值)
而为了避免过拟合,可添加L2正则化,新的损失函数即为:
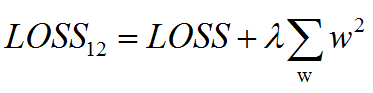
关于反向传播与参数更新可参看这篇博客:https://www.cnblogs.com/wangyong/p/9740170.html
接下来,直接查看代码:
from sklearn import datasets import sklearn import numpy as np import matplotlib.pyplot as plt input_dim=2 #输入维度 output_dim=2 #输出的维度,分类数 epsilon=0.01 #梯度下降算法的学习率 reg_lambda=0.01 def calculate_loss(model,X,y): num_examples=len(X) W1,b1,W2,b2=model['W1'],model['b1'],model['W2'],model['b2'] #正向传播计算预测值 z1=X.dot(W1)+b1 a1=np.tanh(z1) z2=a1.dot(W2)+b2 #Softmax计算概率 exp_scores=np.exp(z2) probs=exp_scores/np.sum(exp_scores,axis=1,keepdims=True) #交叉熵损失 corect_logprobs=-np.log(probs[range(num_examples),y]) data_loss=np.sum(corect_logprobs) #L2正则化 data_loss+=reg_lambda/2*(np.sum(np.square(W1))+np.sum(np.square(W2))) return (1.0/num_examples)*data_loss def predict(model,x): W1,b1,W2,b2=model['W1'],model['b1'],model['W2'],model['b2'] #向前传播 z1=x.dot(W1)+b1 a1=np.tanh(z1) z2=a1.dot(W2)+b2 exp_scores=np.exp(z2) probs=exp_scores/np.sum(exp_scores,axis=1,keepdims=True) return np.argmax(probs,axis=1) def plot_boundary(pred_func,data,labels): x_min,x_max=data[:,0].min()-0.5,data[:,0].max()+0.5 y_min,y_max=data[:,1].min()-0.5,data[:,1].max()+0.5 h=0.01 xx,yy=np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h)) z=pred_func(np.c_[xx.ravel(),yy.ravel()]) z=z.reshape(xx.shape) plt.contourf(xx,yy,z,cmap=plt.cm.Blues,alpha=0.2) plt.scatter(data[:,0],data[:,1],s=40,c=labels,cmap=plt.cm.Vega20c,edgecolors="Black") plt.show() def ANN_model(X,y,nn_dim): num_indim=len(X) #训练数据集 model={} np.random.seed(0) W1=np.random.randn(input_dim,nn_dim)/np.sqrt(input_dim) b1=np.zeros((1,nn_dim)) W2=np.random.randn(nn_dim,output_dim)/np.sqrt(nn_dim) b2=np.zeros((1,output_dim)) #批量梯度下降算法BSGD num_passes=20000 #梯度下降迭代次数 for i in range(0,num_passes): #向前传播 z1=X.dot(W1)+b1 a1=np.tanh(z1) z2=a1.dot(W2)+b2 exp_scores=np.exp(z2) probs=exp_scores/np.sum(exp_scores,axis=1,keepdims=True) #向后传播算法 delta3=probs delta3[range(num_indim),y] -= 1 delta2=delta3.dot(W2.T)*(1-np.power(a1,2)) dW2=(a1.T).dot(delta3) db2=np.sum(delta3,axis=0,keepdims=True) dW1=np.dot(X.T,delta2) db1=np.sum(delta2,axis=0) dW1 += reg_lambda * W1 dW2 += reg_lambda * W2 #更新权重 W1 += -epsilon * dW1 b1 += -epsilon * db1 W2 += -epsilon * dW2 b2 += -epsilon * db2 model={'W1':W1,'b1':b1,'W2':W2,'b2':b2} if i%1000==0: print("Loss after iteration %i:%f",i,calculate_loss(model,X,y)) return model #随机产生的数据 np.random.seed(0) X,y=datasets.make_moons(300,noise=0.25) plt.scatter(X[:,0],X[:,1],s=50,c=y,cmap=plt.cm.Vega20c,edgecolors="Black") plt.title('Medical data') plt.show() hidden_3_model=ANN_model(X,y,3) plot_boundary(lambda x:predict(hidden_3_model,x),X,y) plt.title("Hidden Layer size 3")
运行后的损失值和效果图如下图:


从上图可以看出线性分类与神经网络分类的区别,同时,神经网络的中间隐层的神经元节点数以及隐层的层数均会影响分类效果,可将隐层3个神经元换成其他数量进而查看分类效果。。