在上一次https://www.cnblogs.com/webor2006/p/11530008.html中对二叉树进行了简单的入门,对于上节涉及到的树实用性倒不是太大,但是从今天开始接触的二叉树都是比较有实用价值的,像在JDK8之后很多的结构也都使用到了树,所以学好树是非常有必要的。
二叉排序树开端:
先来看一张二叉排序树的图:
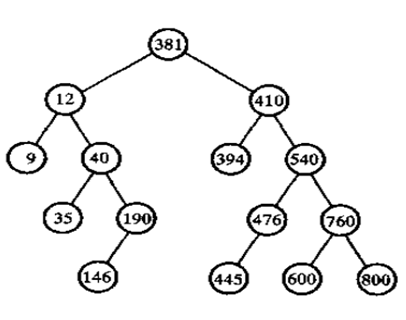
它或者是一颗空树,或者是一颗具有如下性质的树:
1)若左子树不为空,那么左子树上面的所有节点的关键字值都比根节点的关键字值小
2)若右子树不为空,那么右子树上面的所有节点的关键字值都比根节点的关键字值大
3)左右子树都为二叉树
4)没有重复值(这一点在实际中可以忽略)
下面咱们手动来根据上面的规则来画一张二叉排序树,先来对这个树的规则了解清楚,比如数列“5、2、7、3、4、1、6”,下面来让它生成一个二叉排序树:
先拿5作为根结点:

然后再拿2,由于它比5要小,所以放在5的左边:
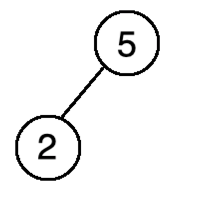
再拿7,由于它比5要大,则放在它的右边:
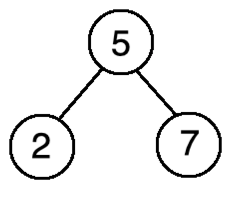
接着再拿3,先跟5比,比它小则往它的左边找,此时则跟2进行对比,由于它比2要大,则放在2的右边,如下:
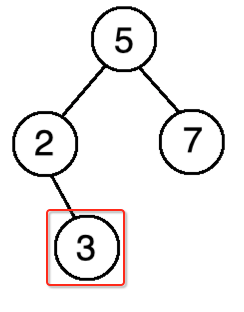
再拿4,它比5小则往左找,到了2,则于它比2要大则继续往它的右边找,则到了3,由于它比3也要大,则将其放到3的右边,如下:

接着再拿1,比5比2都要小,则放在2的左边,如下:
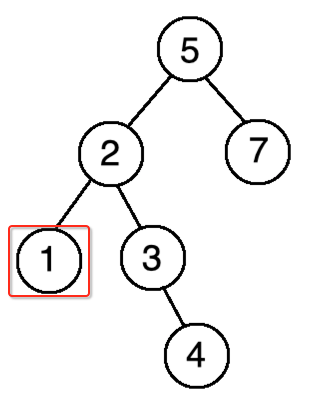
最后6,由于它比5大,则往右找,由于它比7要小,则放到7的左边,最终整个二叉排序树就出来了:
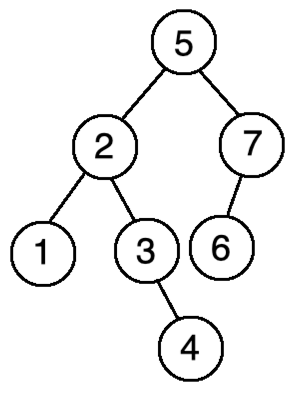
好,如果对上面的树进行一下中序遍历(左中右)的话,其结果会让你吃惊:1、2、3、4、5、6、7,居然取出来的结果就变成有序的了。。
接下来咱们则用代码来生成上面的这棵树,我们之前在定义数的结构时也就是一个数据域,一个左结点,一个右结点,回忆一下:

但是!!此时需要增加一个信息了,也就它的父结点,为啥?这为之后的删除节点做准备,这里可以简单试想一下,假如我们要删除排序二叉树中的这样一个节点:
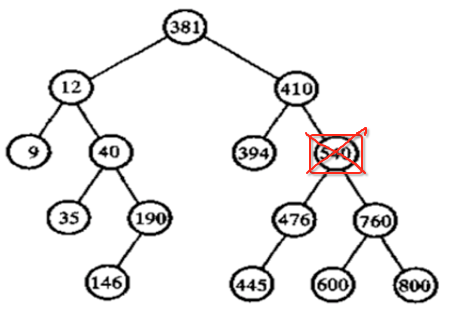
如果要删除的节点木有父节点的信息,请问下面的节点如何链接上它的父节点?所以咱们来定义一下:
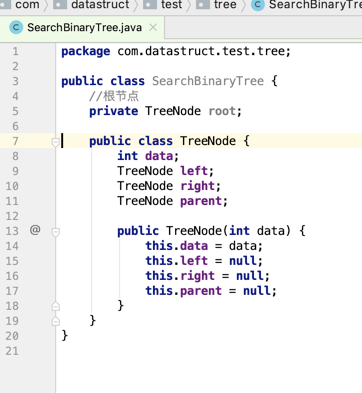
主要操作:
添加节点:
首先定义一个添加方法:
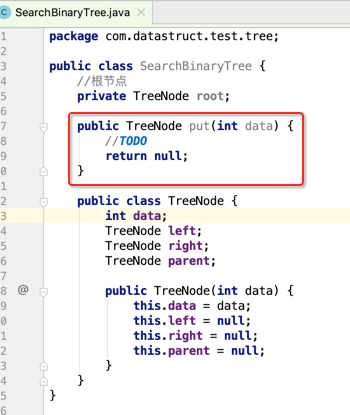
那接下添加肯定有比较大小的过程,首先如果没有根结点,则直接将要添加的数据作为根节点既可,如下:

接下来则是需要进行数据大小比较的,如果该数比节点小则往左找,比它大则往右找,代码如下:

当跳出循环则代表是已经找到待插入元素所存放的位置了,接下来则需要根据这个数据生成一个新节点将其插入到树当中,如下:

遍历:
咱们直接用中序遍历既可,遍历出来就是一个有序数列:

好,接下来咱们来验证一下程序是否写得有问题:
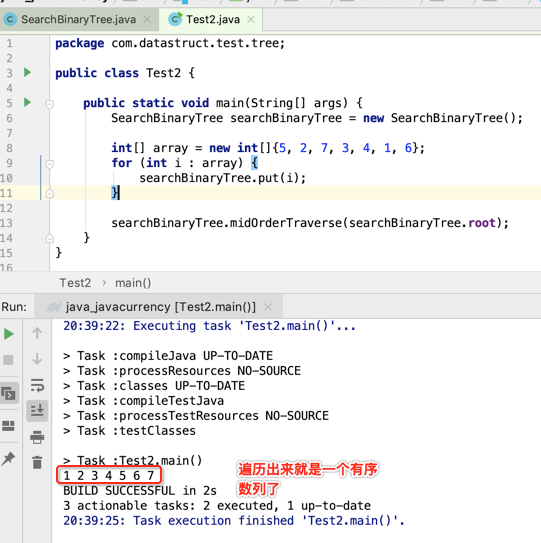
那如果有重复值呢?试一下:
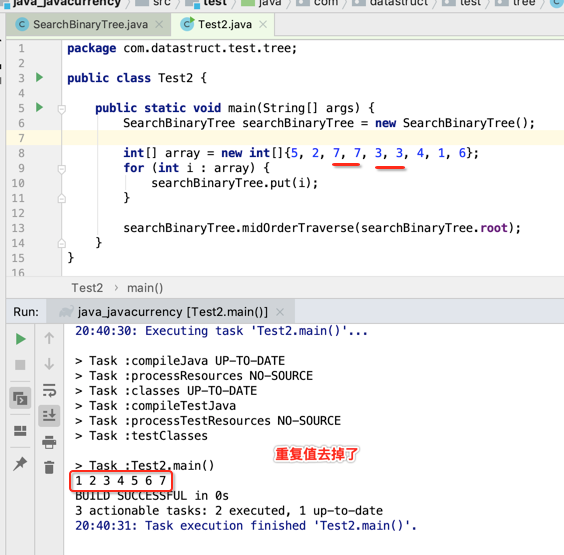
以上就构建了一个去重复值的排序二叉树。
查询节点:
查询就比较简单了,待查找的数比当前结点要小则往左找,则它大则往右找,如下:
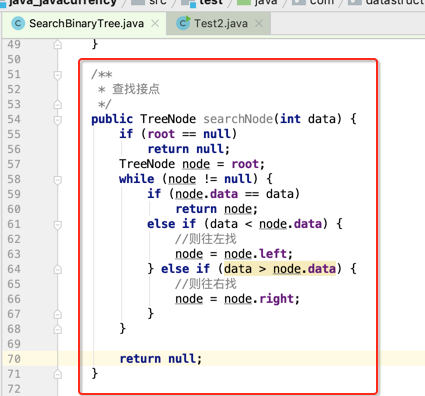
下面来调用一下:
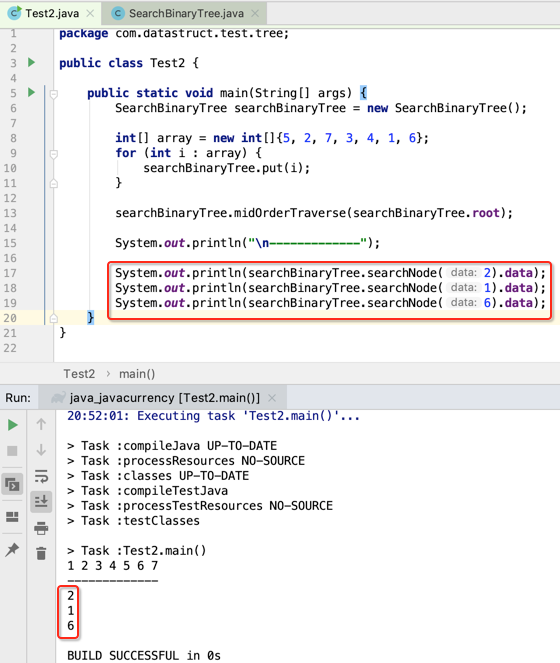
嗯~~确实是木问题,接下来咱们来找一个找不到的值:

删除节点:
接下来最最复杂的操作来了,删除节点。。为啥难呢?下面写着就知道了,总之它有四种情况,下面一个个情况来逐步处理:
①、要删除的节点是叶子节点:比如:
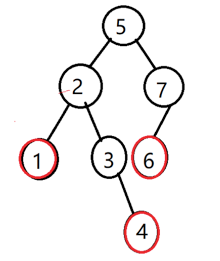
这种情况处理比较简单,只要让父结点的子结点为null既可,如下:

先把整个框架条件定好,接下来先处理第一种情况,先来处理一下特殊情况:如果整棵树就只有一个结点:

其也满足叶子结点的条件,所以可以这样处理:
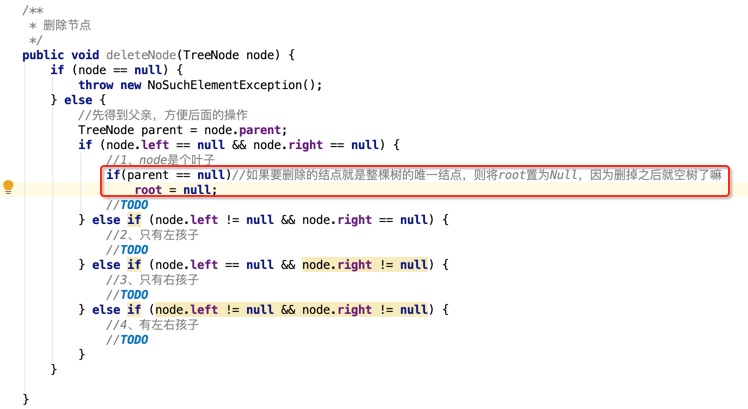
然后再来处理正常叶子的情况:
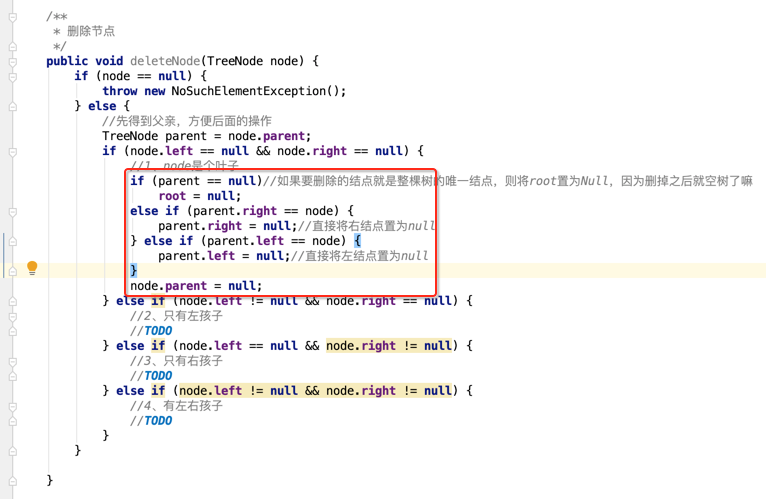
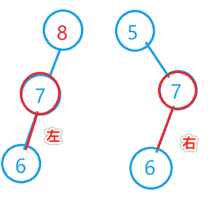
②、要删除的结点它只有左孩子,比如:
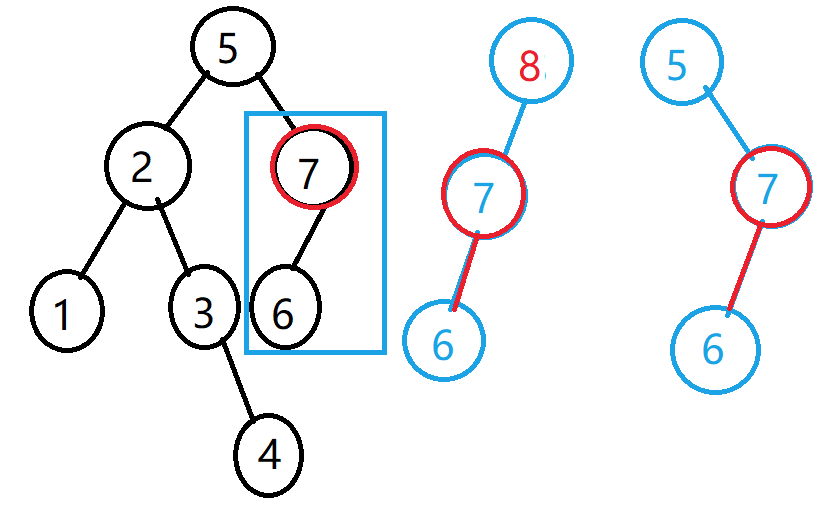
也就是再来处理这个条件分支:
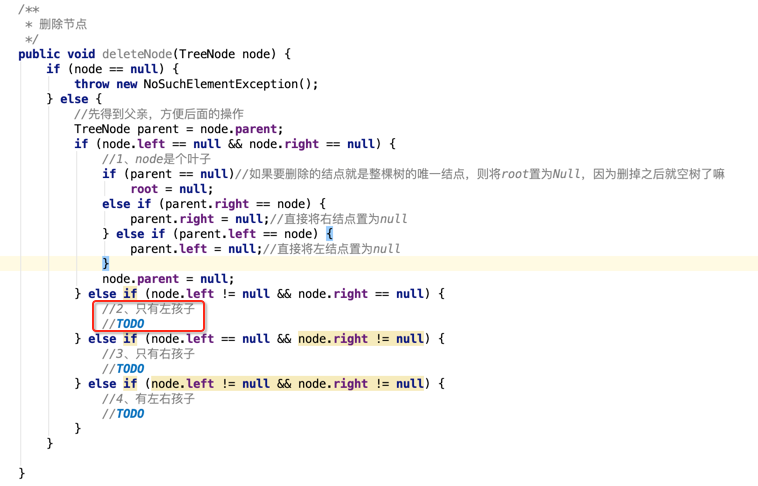
其思路就是需要将要删除结点的左孩子往上顶替回来,也就是说:
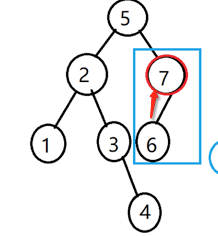
所以看一下具体实现,所先判断是否删的是根结点:
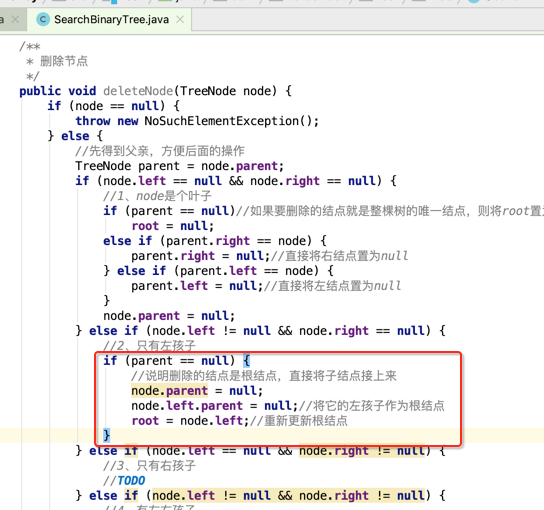
接下来else的条件则是说明要删除的结点不是根结点了,但是此时还存在两种情况,一种是在父节点左边,另一种是在父节点右边,如下:
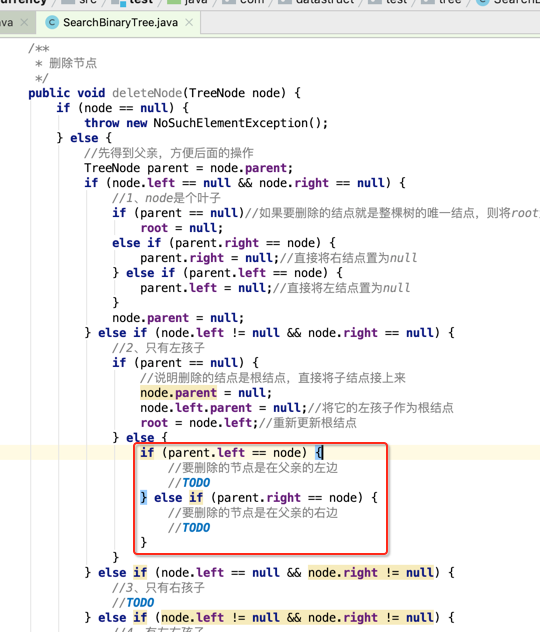
所以代码条件框架如下:
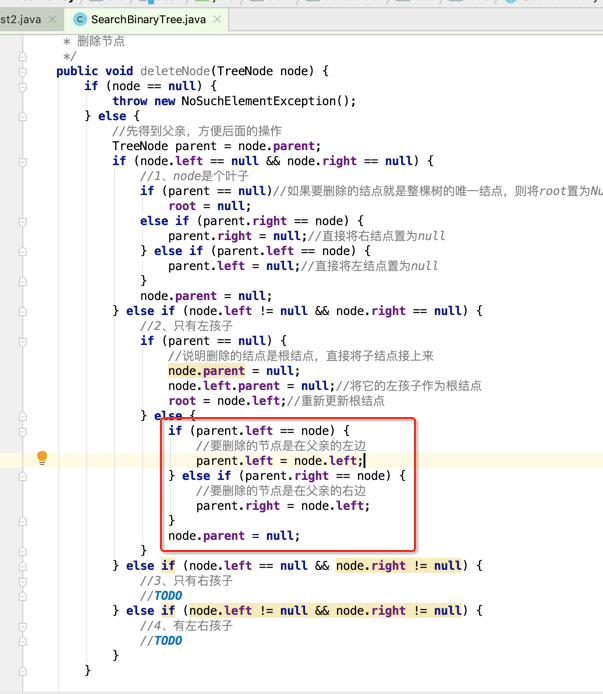
处理也比较简单,直接将要删除结点的左孩子接到父节点上既可,如下:
③、要删除的结点只有右孩子,跟情况2类似。所以直接依葫芦画瓢既可,只是将左孩子统一换成右孩子既可,如下:
/** * 删除节点 */ public void deleteNode(TreeNode node) { if (node == null) { throw new NoSuchElementException(); } else { //先得到父亲,方便后面的操作 TreeNode parent = node.parent; if (node.left == null && node.right == null) { //1、node是个叶子 if (parent == null)//如果要删除的结点就是整棵树的唯一结点,则将root置为Null,因为删掉之后就空树了嘛 root = null; else if (parent.right == node) { parent.right = null;//直接将右结点置为null } else if (parent.left == node) { parent.left = null;//直接将左结点置为null } node.parent = null; } else if (node.left != null && node.right == null) { //2、只有左孩子 if (parent == null) { //说明删除的结点是根结点,直接将子结点接上来 node.parent = null; node.left.parent = null;//将它的左孩子作为根结点 root = node.left;//重新更新根结点 } else { if (parent.left == node) { //要删除的节点是在父亲的左边 parent.left = node.left; } else if (parent.right == node) { //要删除的节点是在父亲的右边 parent.right = node.left; } node.parent = null; } } else if (node.left == null && node.right != null) { //3、只有右孩子 if (parent == null) { //说明删除的结点是根结点,直接将子结点接上来 node.parent = null; node.right.parent = null;//将它的左孩子作为根结点 root = node.right;//重新更新根结点 } else { if (parent.left == node) { //要删除的节点是在父亲的左边 parent.left = node.right; } else if (parent.right == node) { //要删除的节点是在父亲的右边 parent.right = node.right; } node.parent = null; } } else if (node.left != null && node.right != null) { //4、有左右孩子 //TODO } } }
其实代码此时已经有bug了,修改如下:
/** * 删除节点 */ public void deleteNode(TreeNode node) { if (node == null) { throw new NoSuchElementException(); } else { //先得到父亲,方便后面的操作 TreeNode parent = node.parent; if (node.left == null && node.right == null) { //1、node是个叶子 if (parent == null)//如果要删除的结点就是整棵树的唯一结点,则将root置为Null,因为删掉之后就空树了嘛 root = null; else if (parent.right == node) { parent.right = null;//直接将右结点置为null } else if (parent.left == node) { parent.left = null;//直接将左结点置为null } node.parent = null; } else if (node.left != null && node.right == null) { //2、只有左孩子 if (parent == null) { //说明删除的结点是根结点,直接将子结点接上来 node.parent = null; node.left.parent = null;//将它的左孩子作为根结点 root = node.left;//重新更新根结点 } else { if (parent.left == node) { //要删除的节点是在父亲的左边 node.left.parent = parent; parent.left = node.left; } else if (parent.right == node) { //要删除的节点是在父亲的右边 node.left.parent = parent; parent.right = node.left; } node.parent = null; } } else if (node.left == null && node.right != null) { //3、只有右孩子 if (parent == null) { //说明删除的结点是根结点,直接将子结点接上来 node.parent = null; node.right.parent = null;//将它的左孩子作为根结点 root = node.right;//重新更新根结点 } else { if (parent.left == node) { //要删除的节点是在父亲的左边 node.right.parent = parent; parent.left = node.right; } else if (parent.right == node) { //要删除的节点是在父亲的右边 node.right.parent = parent; parent.right = node.right; } node.parent = null; } } else if (node.left != null && node.right != null) { //4、有左右孩子 //TODO } } }
④、要删除的结点既有左孩子,又有右孩子。比如:
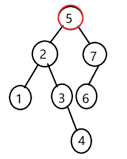
也就是对应这个条件的代码:
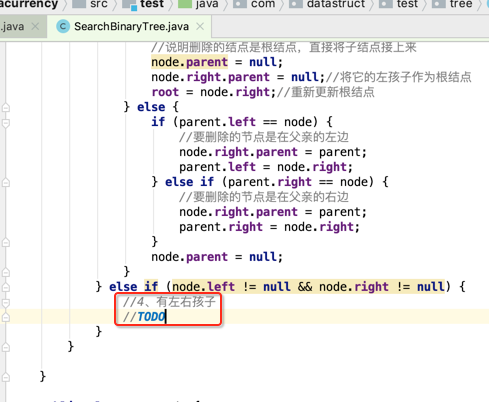
此时最复杂的操作来了,下面得留个心,很容易写错的,因为涉及到的情况也挺多的,下面一个个情况进行分析然后进行一一处理:
情况一:
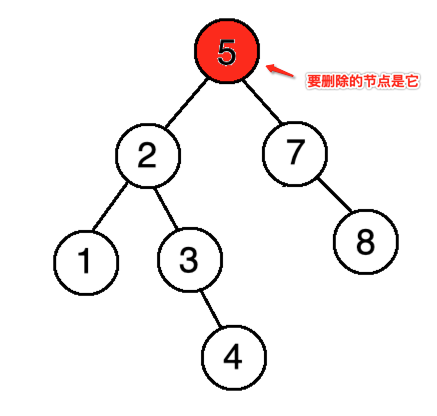
那此时删掉之后,得由7往上补,因为都了右结点,都比左边的数要大,所以最终形态会是:
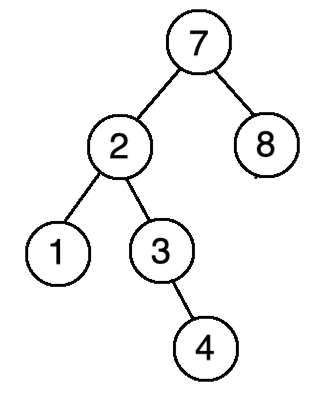
那下面用代码来处理这种情况:
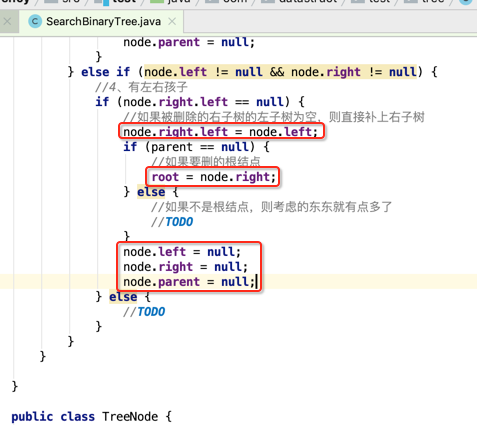
这里还有一种情况如下:
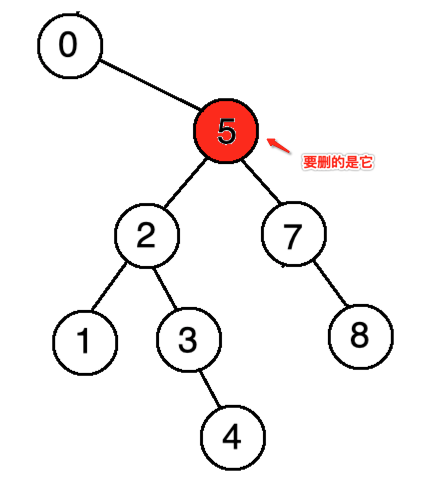
也就是要删除的节点不是根节点,那此时则直接将7往上替换既可,如下:
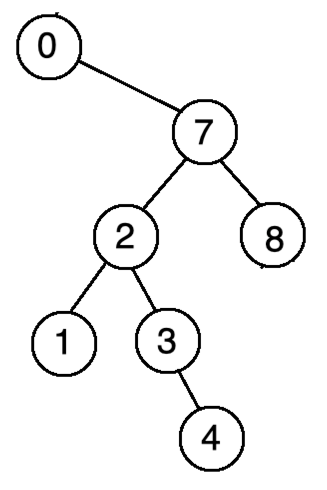
所以这块逻辑的代码比较简单:

类似的,还有可能在根结点左边,如下:

像这种处理也是类似,直接将7顶替上来既可:

所以相似的处理代码:
情况二:
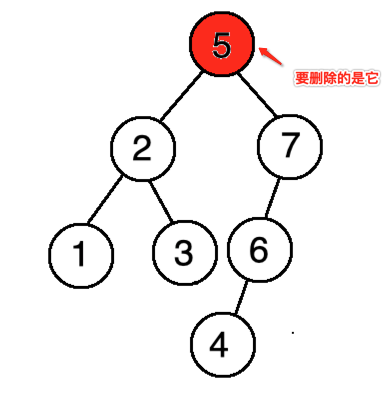
此时就要注意啦,就不能直接将7给被上去了啦,为啥,假如把7替上去,就不符合排序二叉树了?所以应该是遍历它的左孩子将其最小的4顶上去,如下:
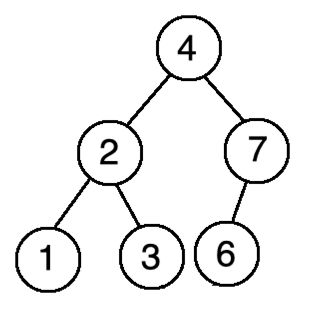
所以下面来实现一下,先来封装一下找节点最小值的方法:

此时也就是找到了这个结点了:
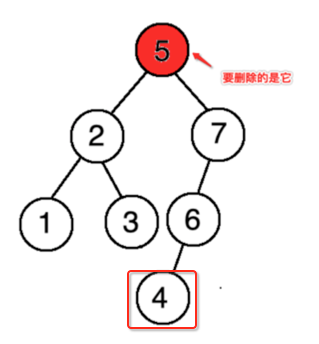
接下来则需要将这个4放到5的位置,如何做呢?先这样做:
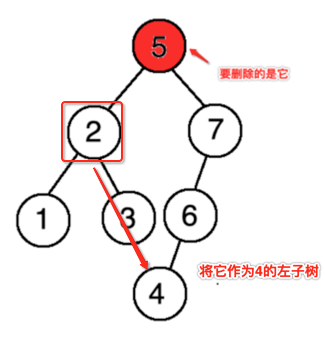
所以先处理这种情况,得一个个来,不然很容易绕晕的,而且必须要画图,具体代码如下:
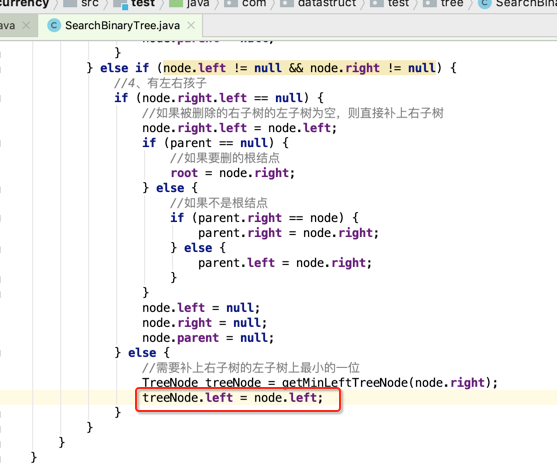
此时的形态就变为:
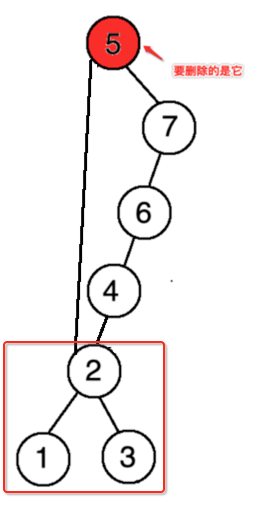
好,接下来需要对最小节点做引用处理,因为有可能在它下面还有树,比如:
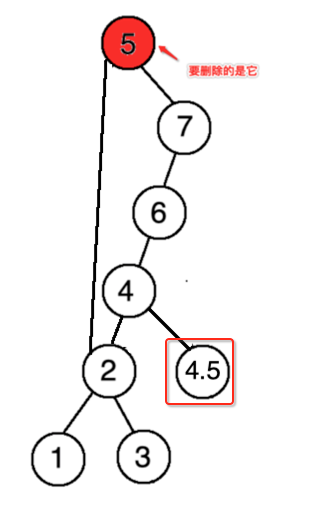
此时则需要将4这棵最小的值的右子树得先处理好了,才能将4作为根节点,所以代码处理如下:
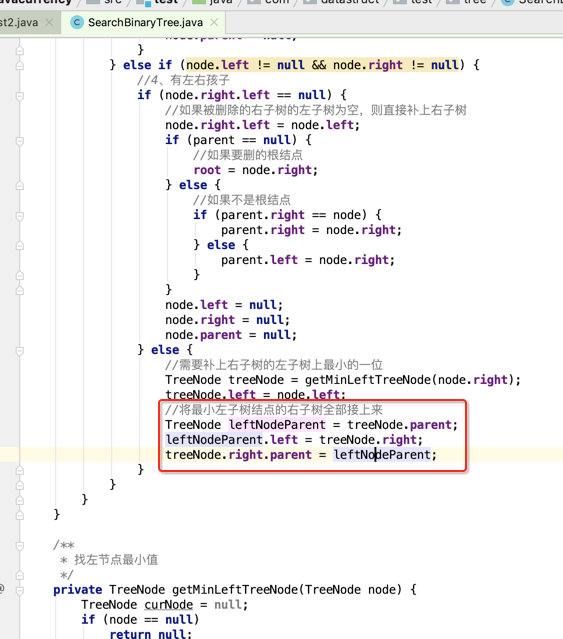
所以此时的形态就变为:

注意需要将4的父结点的引用给去掉,以便将4顶上去,所以修改一下代码:
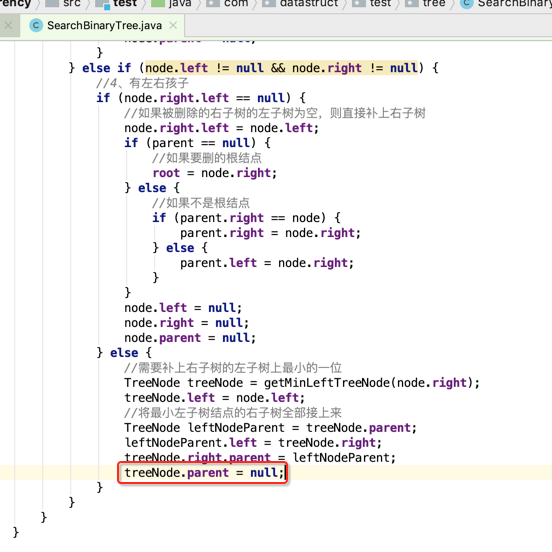
好,接下来再处理第三步,则应该是将7作为4的右子树,形态就会变为:

所以这一步的代码为:

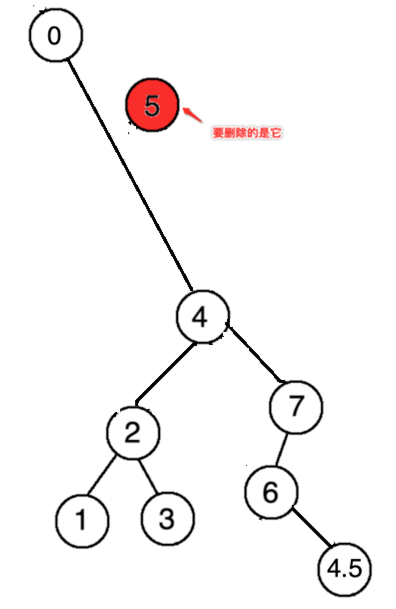
同样的它也有一种特殊情况,比如要删的这个节点不是根结点,如下:
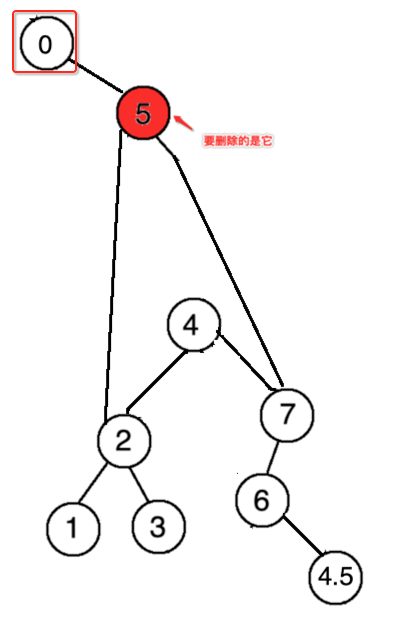
此时直接将4接到根结点既可,如下:
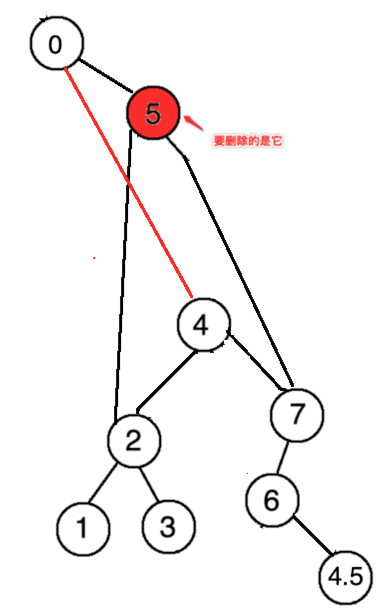
所以代码如下:
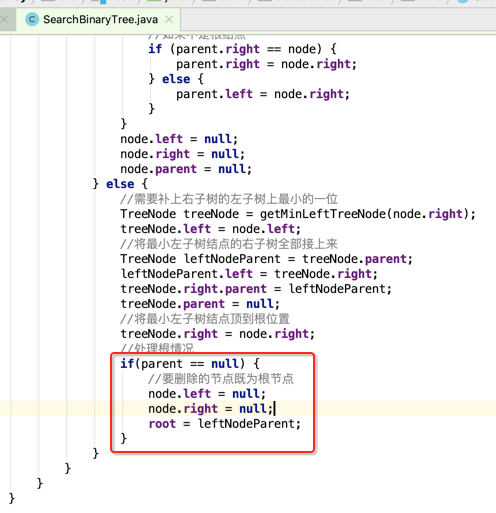
此时处理的是根结点的情况,也就是形态会成了这样了:
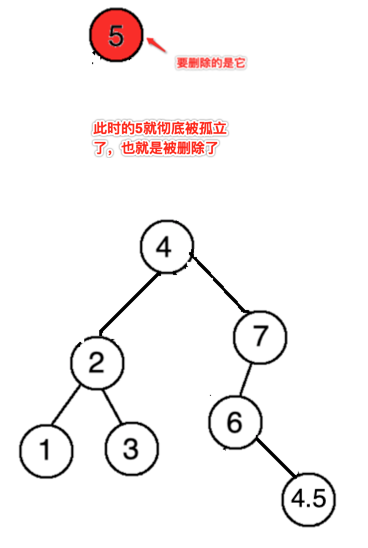
接下来再来处理有父节点的:
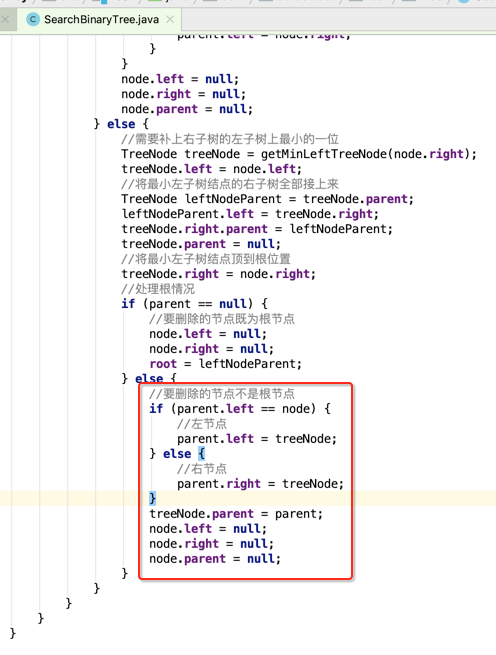
有父节点的就有两种情况,一个是被删除的子节点位于父节点左边,一个是位于父节点右边,下面以位于父节点右边为例来看一下目前的形态:
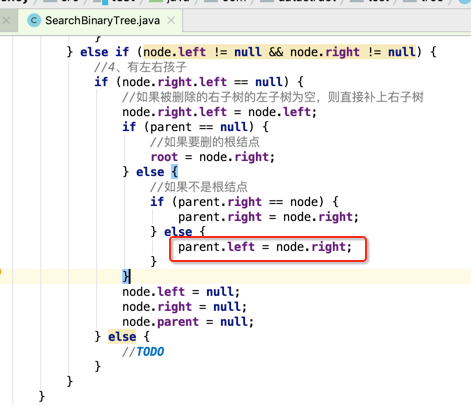
于是乎,整个删除节点的代码如下:
/** * 删除节点 */ public void deleteNode(TreeNode node) { if (node == null) { throw new NoSuchElementException(); } else { //先得到父亲,方便后面的操作 TreeNode parent = node.parent; if (node.left == null && node.right == null) { //1、node是个叶子 if (parent == null)//如果要删除的结点就是整棵树的唯一结点,则将root置为Null,因为删掉之后就空树了嘛 root = null; else if (parent.right == node) { parent.right = null;//直接将右结点置为null } else if (parent.left == node) { parent.left = null;//直接将左结点置为null } node.parent = null; } else if (node.left != null && node.right == null) { //2、只有左孩子 if (parent == null) { //说明删除的结点是根结点,直接将子结点接上来 node.parent = null; node.left.parent = null;//将它的左孩子作为根结点 root = node.left;//重新更新根结点 } else { if (parent.left == node) { //要删除的节点是在父亲的左边 node.left.parent = parent; parent.left = node.left; } else if (parent.right == node) { //要删除的节点是在父亲的右边 node.left.parent = parent; parent.right = node.left; } node.parent = null; } } else if (node.left == null && node.right != null) { //3、只有右孩子 if (parent == null) { //说明删除的结点是根结点,直接将子结点接上来 node.parent = null; node.right.parent = null;//将它的左孩子作为根结点 root = node.right;//重新更新根结点 } else { if (parent.left == node) { //要删除的节点是在父亲的左边 node.right.parent = parent; parent.left = node.right; } else if (parent.right == node) { //要删除的节点是在父亲的右边 node.right.parent = parent; parent.right = node.right; } node.parent = null; } } else if (node.left != null && node.right != null) { //4、有左右孩子 if (node.right.left == null) { //如果被删除的右子树的左子树为空,则直接补上右子树 node.right.left = node.left; if (parent == null) { //如果要删的根结点 root = node.right; } else { //如果不是根结点 if (parent.right == node) { parent.right = node.right; } else { parent.left = node.right; } } node.left = null; node.right = null; node.parent = null; } else { //需要补上右子树的左子树上最小的一位 TreeNode treeNode = getMinLeftTreeNode(node.right); treeNode.left = node.left; //将最小左子树结点的右子树全部接上来 TreeNode leftNodeParent = treeNode.parent; leftNodeParent.left = treeNode.right; treeNode.right.parent = leftNodeParent; treeNode.parent = null; //将最小左子树结点顶到根位置 treeNode.right = node.right; //处理根情况 if (parent == null) { //要删除的节点既为根节点 node.left = null; node.right = null; root = leftNodeParent; } else { //要删除的节点不是根节点 if (parent.left == node) { //左节点 parent.left = treeNode; } else { //右节点 parent.right = treeNode; } treeNode.parent = parent; node.left = null; node.right = null; node.parent = null; } } } } }
真的是。。晕菜了~~太TM复杂了,下面先来论证一下是否写得靠谱:
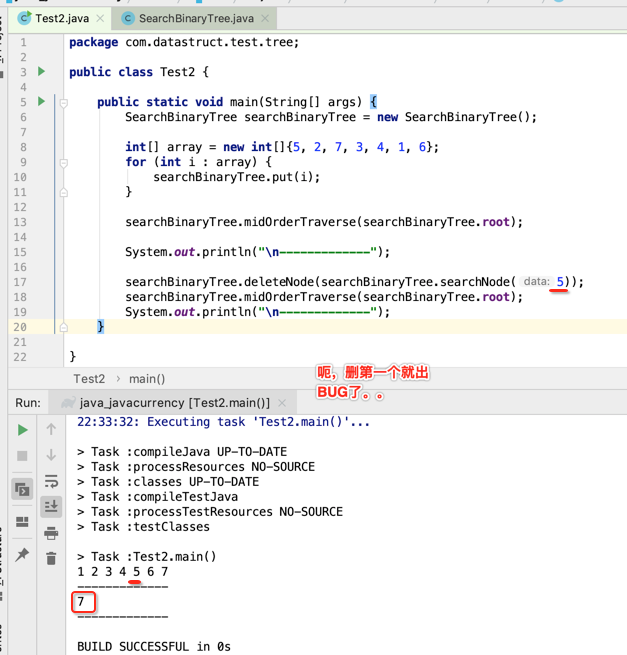
真是实力打脸,得找bug了。。
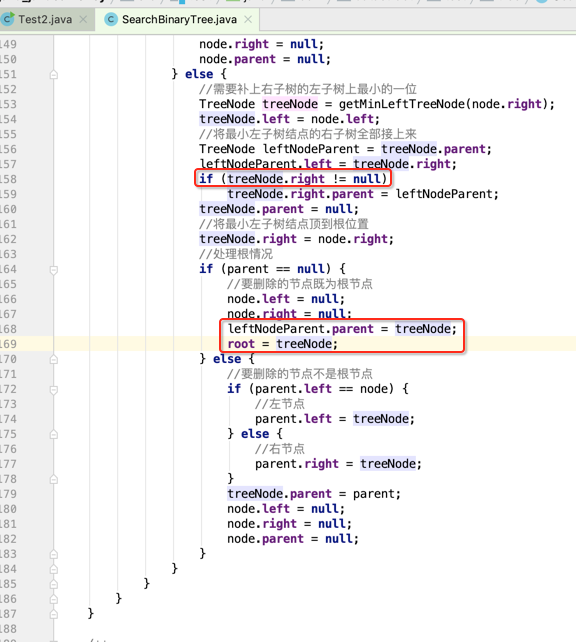
再运行:
嗯,对了,再来测:
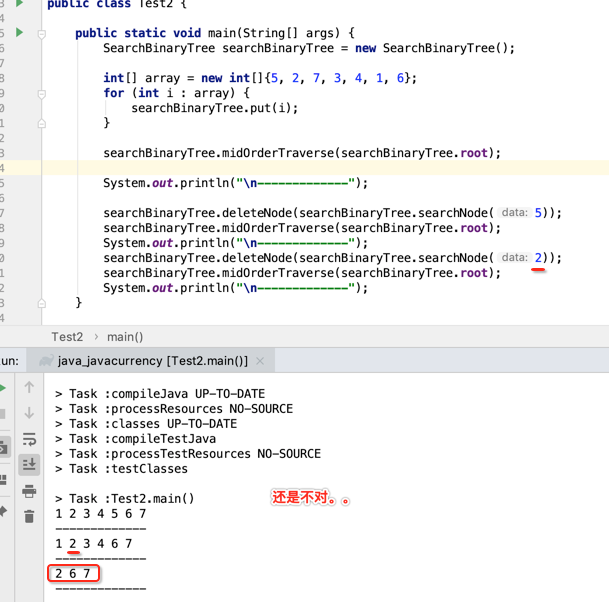
继续找bug:
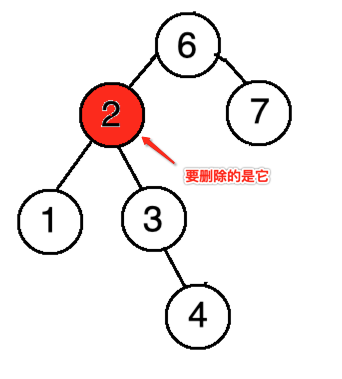
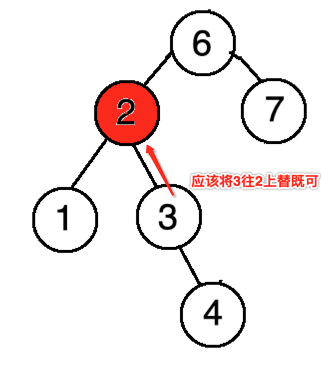
下面看一下为啥输出不对了,调一下:
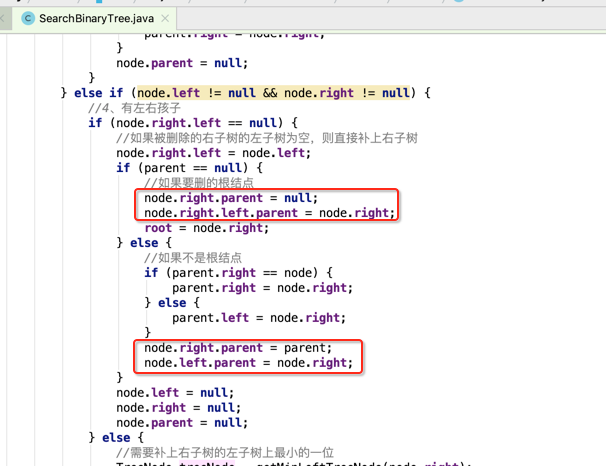
另外,在删2时,发现它的parent还是5,不太对,所以得继续找原因,发现是这块的问题:

再运行:
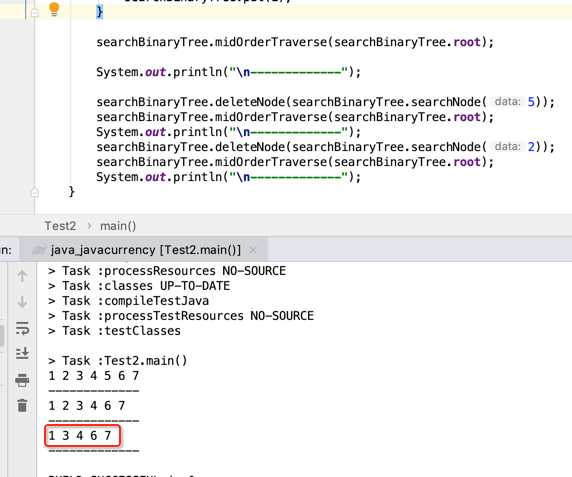
正确了,可见这块删除只要有一个关系没处理好其结果就会有问题,面试要谁问到手写它,我觉得没个几个小时肯定是很难写得非常正确的,好下面继续再测试:
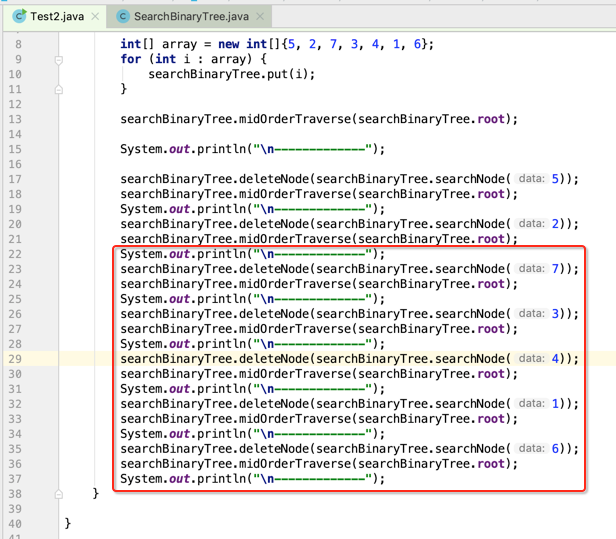
看一下结果:
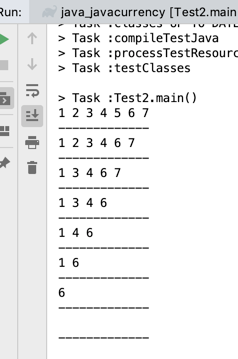
哇塞,真不容易~~完美!!最后代码定格在:
package com.datastruct.test.tree; import java.util.NoSuchElementException; public class SearchBinaryTree { //根节点 TreeNode root; public TreeNode put(int data) { if (root == null) {//如果没有根节点,则直接将其作为根节点 TreeNode node = new TreeNode(data); root = node; return root; } TreeNode parent = null; TreeNode node = root; while (node != null) { parent = node;//再往下移之前需要记录一下父元素,以便在找到要插入的位置时将其进行连接上 if (data < node.data) { //则往左找 node = node.left; } else if (data > node.data) { //则往右找 node = node.right; } else { //如果已经有相同的重复节点了,则直接返回,因为二叉排序树是不允许重复的 return node; } } //生成一个新节点将其插入 TreeNode newNode = new TreeNode(data); if (data < parent.data) { parent.left = newNode; } else { parent.right = newNode; } newNode.parent = parent; return newNode; } /** * 中序遍历 */ public void midOrderTraverse(TreeNode root) { if (root == null) return; midOrderTraverse(root.left); System.out.print(root.data + " "); midOrderTraverse(root.right); } /** * 查找接点 */ public TreeNode searchNode(int data) { if (root == null) return null; TreeNode node = root; while (node != null) { if (node.data == data) return node; else if (data < node.data) { //则往左找 node = node.left; } else if (data > node.data) { //则往右找 node = node.right; } } return null; } /** * 删除节点 */ public void deleteNode(TreeNode node) { if (node == null) { throw new NoSuchElementException(); } else { //先得到父亲,方便后面的操作 TreeNode parent = node.parent; if (node.left == null && node.right == null) { //1、node是个叶子 if (parent == null)//如果要删除的结点就是整棵树的唯一结点,则将root置为Null,因为删掉之后就空树了嘛 root = null; else if (parent.right == node) { parent.right = null;//直接将右结点置为null } else if (parent.left == node) { parent.left = null;//直接将左结点置为null } node.parent = null; } else if (node.left != null && node.right == null) { //2、只有左孩子 if (parent == null) { //说明删除的结点是根结点,直接将子结点接上来 node.parent = null; node.left.parent = null;//将它的左孩子作为根结点 root = node.left;//重新更新根结点 } else { if (parent.left == node) { //要删除的节点是在父亲的左边 node.left.parent = parent; parent.left = node.left; } else if (parent.right == node) { //要删除的节点是在父亲的右边 node.left.parent = parent; parent.right = node.left; } node.parent = null; } } else if (node.left == null && node.right != null) { //3、只有右孩子 if (parent == null) { //说明删除的结点是根结点,直接将子结点接上来 node.parent = null; node.right.parent = null;//将它的左孩子作为根结点 root = node.right;//重新更新根结点 } else { if (parent.left == node) { //要删除的节点是在父亲的左边 node.right.parent = parent; parent.left = node.right; } else if (parent.right == node) { //要删除的节点是在父亲的右边 node.right.parent = parent; parent.right = node.right; } node.parent = null; } } else if (node.left != null && node.right != null) { //4、有左右孩子 if (node.right.left == null) { //如果被删除的右子树的左子树为空,则直接补上右子树 node.right.left = node.left; if (parent == null) { //如果要删的根结点 node.right.parent = null; node.right.left.parent = node.right; root = node.right; } else { //如果不是根结点 if (parent.right == node) { parent.right = node.right; } else { parent.left = node.right; } node.right.parent = parent; node.left.parent = node.right; } node.left = null; node.right = null; node.parent = null; } else { //需要补上右子树的左子树上最小的一位 TreeNode treeNode = getMinLeftTreeNode(node.right); treeNode.left = node.left; node.left.parent = treeNode; //将最小左子树结点的右子树全部接上来 TreeNode leftNodeParent = treeNode.parent; leftNodeParent.left = treeNode.right; if (treeNode.right != null) treeNode.right.parent = leftNodeParent; treeNode.parent = null; //将最小左子树结点顶到根位置 treeNode.right = node.right; //处理根情况 if (parent == null) { //要删除的节点既为根节点 node.left = null; node.right = null; leftNodeParent.parent = treeNode; root = treeNode; } else { //要删除的节点不是根节点 if (parent.left == node) { //左节点 parent.left = treeNode; } else { //右节点 parent.right = treeNode; } treeNode.parent = parent; node.left = null; node.right = null; node.parent = null; } } } } } /** * 找左节点最小值 */ private TreeNode getMinLeftTreeNode(TreeNode node) { TreeNode curNode = null; if (node == null) return null; else { curNode = node; while (curNode.left != null) { curNode = curNode.left; } } return curNode; } public class TreeNode { int data; TreeNode left; TreeNode right; TreeNode parent; public TreeNode(int data) { this.data = data; this.left = null; this.right = null; this.parent = null; } } }