矩阵描述

题目描述

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

 

比如n=3时，2*3的矩形块有3种覆盖方法：

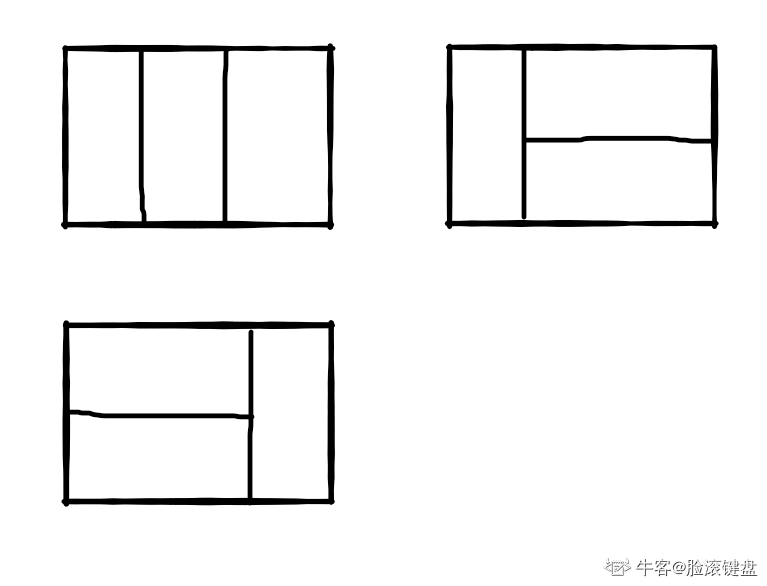
思路：

　　当n= 1时，有F(1) = 1种方法

　　当n = 2时, 有F(2) = 2种方法

　　当n = 3时，有F(3) = 3 = F(1) + F(2)种方法

　　当n = 4时，有F(4) = F(3) + F(2) +F(1) = 8种方法

　　。。。

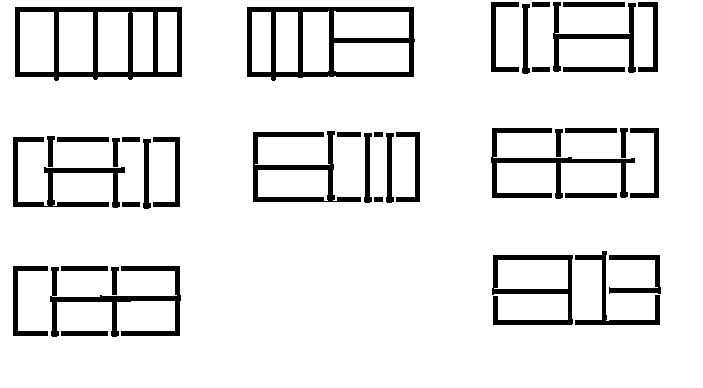
　　当n = n 时，会有F(n) = F(n -1) + F(n -2) +....+F(0)

　　是的，这又是一个斐波那契数列

递归法：

class Solution {
public:
    int rectCover(int number) {
        if(number == 0)
            return 0;
        if(number == 1)
            return 1;
        if(number == 2)
            return 2;
        return rectCover(number - 1) + rectCover(number - 2);
    }
};

动态规划法：

class Solution {
public:
    int rectCover(int number) {
        if(number == 0)
            return 0;
        if(number == 1)
            return 1;
        if(number == 2)
            return 2;
       int *sum = new int[number+1]();
        sum[1] = 1;
        sum[2] = 2;
        for(int i = 3;i <= number;i++)
        {
            sum[i] = sum[i - 1] + sum[i - 2];
        }
        return sum[number];
    }
};