插入操作:
RB-INSERT(T, z)
1 y ← nil[T] // y 始终指向 x 的父结点。
2 x ← root[T] // x 指向当前树的根结点,
3 while x ≠ nil[T]
4 do y ← x
5 if key[z] < key[x] //向左,向右..
6 then x ← left[x]
7 else x ← right[x] // 为了找到合适的插入点,x 探路跟踪路径,直到x成为NIL 为止。
8 p[z] ← y // y置为 插入结点z 的父结点。
9 if y = nil[T]
10 then root[T] ← z
11 else if key[z] < key[y]
12 then left[y] ← z
13 else right[y] ← z //此 8-13行,置z 相关的指针。
14 left[z] ← nil[T]
15 right[z] ← nil[T] //设为空,
16 color[z] ← RED //将新插入的结点z作为红色
17 RB-INSERT-FIXUP(T, z) //因为将z着为红色,可能会违反某一红黑性质,
//所以需要调用RB-INSERT-FIXUP(T, z)来保持红黑性质。
17 行的RB-INSERT-FIXUP(T, z) ,在下文会得到着重而具体的分析。
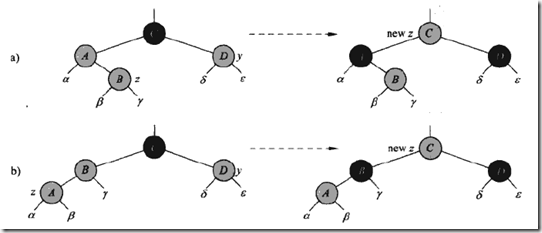
可以看到插入操作在调用Fixup之前,只是简单的将新节点置为红色,并按照二叉查找树的方式插入到书中,所引起的对RB树规则的破坏由Fixup处理。下面分析插入操作会产生什么样的情形。首先,新节点z是红色的,则其父节点p(z)有可能是红色或者黑色,或者没有父节点:
- 如果p(z)是黑色的,那没有规则被破坏;
- 如果p(z)是红色的,那破坏了规则4,p(p(z))只能是黑色(因为如果是红色,会破坏规则4,而除新节点外都是满足RB树规则的),p(p(z))的另外一个孩子可能是红色(设其为Case1),也可能是黑色(设其为Case2);
- 如果p(z)是空,那就直接将z改为黑色的就可以了;
对于Case1,处理方法是将p(p(z))改为红色,p(p(z))的两个孩子节点改为黑色,z依然是红色,则以p(p(z))为根的子树满足RB树规则,但p(p(z))的p可不一定是黑色。所以我们之后调整的是p(p(z))为根的子树,令z=p(p(z))。则如果p(z)是红色,z是红色依然会破坏规则4,因为同样是违反规则4,则继续上面的分析,如果是Case1,则按照Case1的方法执行,如果是Case2,则按照Case2的方法走。
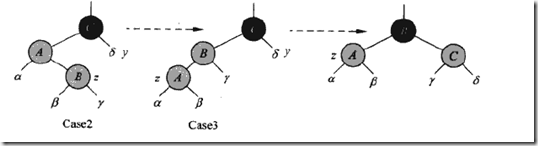
对于Case2,事实上z的叔叔节点是黑色的时候还有两种情况:(1)z是p(z)的右孩子和(2)z是p(z)的左孩子。(1)做一个左旋就可以变成(2),而(2)做一个右旋就可以变成(1)。所以我们只要能找到其中之一的解法就可以了。 下面的图来源于《算法导论》,可以看到(2)可以通过对B做左旋完成。
下面再来分析删除操作:(在BST的删除操作中,需要考虑3种情况,z是叶子节点;z有一个子女;z有两个子女,如果z有0或者1个子女,那么可以直接删除z;若有2个子女,则需要删除z的后继,并将后继中的数据拷贝到z所在的空间中)
RB-DELETE(T, z)
1 if left[z] = nil[T] or right[z] = nil[T]
2 then y ← z
3 else y ← TREE-SUCCESSOR(z) // y是真正要被移除的那个节点
4 if left[y] ≠ nil[T]
5 then x ← left[y]
6 else x ← right[y]
7 p[x] ← p[y] // x有可能是空的;
8 if p[y] = nil[T] // 如果y是root节点,需要调整树的root为x
9 then root[T] ← x
10 else if y = left[p[y]] //将x放到正确的位置
11 then left[p[y]] ← x
12 else right[p[y]] ← x
13 if y ≠ z // copy数据
14 then key[z] ← key[y]
15 copy y's satellite data into z
16 if color[y] = BLACK //如果y是黑色的,
17 then RB-DELETE-FIXUP(T, x) //则调用RB-DELETE-FIXUP(T, x)
18 return y
删除操作跟二叉搜索树的删除类似,最大的差别就在于需要维护RB树的性质。下面我们按照各种情况来分析:
1)每个结点要么是红的,要么是黑的。
2)根结点是黑的。
3)每个叶结点,即空结点(NIL)是黑的。
4)如果一个结点是红的,那么它的俩个儿子都是黑的。
5)对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
如果我们删除一个红色节点,它的父亲和儿子一定是黑色的。所以我们可以简单的用它的黑色儿子替换它,并不会破坏属性3和4。通过被删除节点的所有路径只是少了一个红色节点,这样可以继续保证属性5。
另一种简单情况是在被删除节点是黑色而它的儿子是红色的时候。如果只是去除这个黑色节点,用它的红色儿子顶替上来的话,会破坏属性4,但是如果我们重绘它的儿子为黑色,则曾经通过它的所有路径将通过它的黑色儿子,这样可以继续保持属性4。
需要进一步讨论的是在要删除的节点和它的儿子二者都是黑色的时候,这是一种复杂的情况。我们首先把要删除的节点替换为它的儿子。出于方便,称呼这个儿子为N(x),称呼它的兄弟(它父亲的另一个儿子)为S(w)。在下面的示意图中,我们还是使用P称呼N的父亲,SL称呼S的左儿子,SR称呼S的右儿子。
如果N(x)和它初始的父亲是黑色,则删除它的父亲导致通过N(x)的路径都比不通过它的路径少了一个黑色节点。因为这违反了属性 4,树需要被重新平衡。有几种情况需要考虑:
情况 1: N 是新的根。在这种情况下,我们就做完了。我们从所有路径去除了一个黑色节点,而新根是黑色的,所以属性都保持着。
注意: 在情况2、5和6下,我们假定 N 是它父亲的左儿子。如果它是右儿子,则在这些情况下的左和右应当对调。
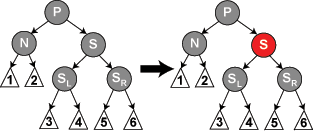
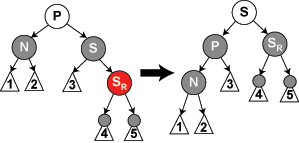
情况 2: S 是红色。在这种情况下我们在N的父亲上做左旋转,把红色兄弟转换成N的祖父。我们接着对调 N 的父亲和祖父的颜色。尽管所有的路径仍然有相同数目的黑色节点,现在 N 有了一个黑色的兄弟和一个红色的父亲,所以我们可以接下去按 4、5或6情况来处理。(它的新兄弟是黑色因为它是红色S的一个儿子。)
情况 3: N 的父亲、S 和 S 的儿子都是黑色的。在这种情况下,我们简单的重绘 S 为红色。结果是通过S的所有路径, 它们就是以前不通 过 N 的那些路径,都少了一个黑色节点。因为删除 N 的初始的父亲使通过 N 的所有路径少了一个黑色节点,这使事情都平衡了起来。但是,通过 P 的所有路径现在比不通过 P 的路径少了一个黑色节点,所以仍然违反属性4。要修正这个问题,我们要从情况 1 开始,在 P 上做重新平衡处理。
情况 4: S 和 S 的儿子都是黑色,但是 N 的父亲是红色。在这种情况下,我们简单的交换 N 的兄弟和父亲的颜色。这不影响不通过 N 的路径的黑色节点的数目,但是它在通过 N 的路径上对黑色节点数目增加了一,添补了在这些路径上删除的黑色节点。
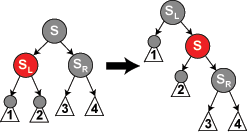
情况 5: S 是黑色,S 的左儿子是红色,S 的右儿子是黑色,而 N 是它父亲的左儿子。在这种情况下我们在 S 上做右旋转,这样 S 的左儿子成为 S 的父亲和 N 的新兄弟。我们接着交换 S 和它的新父亲的颜色。所有路径仍有同样数目的黑色节点,但是现在 N 有了一个右儿子是红色的黑色兄弟,所以我们进入了情况 6。N 和它的父亲都不受这个变换的影响。
情况 6: S 是黑色,S 的右儿子是红色,而 N 是它父亲的左儿子。在这种情况下我们在 N 的父亲上做左旋转,这样 S 成为 N 的父亲和 S 的右儿子的父亲。我们接着交换 N 的父亲和 S 的颜色,并使 S 的右儿子为黑色。子树在它的根上的仍是同样的颜色,所以属性 3 没有被违反。但是,N 现在增加了一个黑色祖先: 要幺 N 的父亲变成黑色,要么它是黑色而 S 被增加为一个黑色祖父。所以,通过 N 的路径都增加了一个黑色节点。
此时,如果一个路径不通过 N,则有两种可能性:
- 它通过 N 的新兄弟。那么它以前和现在都必定通过 S 和 N 的父亲,而它们只是交换了颜色。所以路径保持了同样数目的黑色节点。
- 它通过 N 的新叔父,S 的右儿子。那么它以前通过 S、S 的父亲和 S 的右儿子,但是现在只通过 S,它被假定为它以前的父亲的颜色,和 S 的右儿子,它被从红色改变为黑色。合成效果是这个路径通过了同样数目的黑色节点。
在任何情况下,在这些路径上的黑色节点数目都没有改变。所以我们恢复了属性 4。在示意图中的白色节点可以是红色或黑色,但是在变换前后都必须指定相同的颜色。
http://huzunwen2008.blog.163.com/blog/static/29635207200710852053727/