Description
Today we play a squiggly sudoku, The objective is to fill a 9*9 grid with digits so that each column, each row, and each of the nine Connecting-sub-grids that compose the grid contains all of the digits from 1 to 9.
Left figure is the puzzle and right figure is one solution.
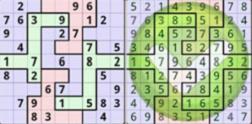
Now, give you the information of the puzzle, please tell me is there no solution or multiple solution or one solution.
Left figure is the puzzle and right figure is one solution.

Now, give you the information of the puzzle, please tell me is there no solution or multiple solution or one solution.
还是数独问题,其实和前面的没有什么两样,然后对于每个奇形怪状的9格子,我是用BFS来构造的。。。。。。
代码如下:

#include<iostream> #include<cstring> #include<cstdio> #include<queue> using namespace std; const int MaxN=800; const int MaxM=350; const int MaxNode=MaxN*MaxM; int map1[10][10]; struct DLX { int U[MaxNode],D[MaxNode],L[MaxNode],R[MaxNode],col[MaxNode],row[MaxNode]; int size,n,m; int H[MaxN],S[MaxM]; int ans[100],ans1[100],anst[100]; int ansnum,depth; void init(int _n,int _m) { ansnum=0; n=_n; m=_m; for(int i=0;i<=m;++i) { U[i]=D[i]=i; L[i]=i-1; R[i]=i+1; row[i]=0; S[i]=0; } L[0]=m; R[m]=0; size=m; for(int i=1;i<=n;++i) H[i]=-1; } void Link(int r,int c) { col[++size]=c; row[size]=r; ++S[c]; U[size]=U[c]; D[size]=c; D[U[c]]=size; U[c]=size; if(H[r]==-1) H[r]=L[size]=R[size]=size; else { L[size]=L[H[r]]; R[size]=H[r]; R[L[H[r]]]=size; L[H[r]]=size; } } void remove(int c) { L[R[c]]=L[c]; R[L[c]]=R[c]; for(int i=D[c];i!=c;i=D[i]) for(int j=R[i];j!=i;j=R[j]) { U[D[j]]=U[j]; D[U[j]]=D[j]; --S[col[j]]; } } void resume(int c) { for(int i=U[c];i!=c;i=U[i]) for(int j=L[i];j!=i;j=L[j]) { U[D[j]]=j; D[U[j]]=j; ++S[col[j]]; } L[R[c]]=R[L[c]]=c; } void showans() { for(int i=0;i<depth;++i) ans1[(anst[i]-1)/9+1]=(anst[i]-1)%9+1; for(int i=1;i<=81;++i) { cout<<ans1[i]; if(i%9==0) cout<<endl; } } void copyans() { for(int i=0;i<100;++i) anst[i]=ans[i]; } bool Dance(int d) { if(R[0]==0) { depth=d; if(ansnum) { ++ansnum; return 1; } ++ansnum; copyans(); return 0; } int c=R[0]; for(int i=R[0];i!=0;i=R[i]) if(S[i]<S[c]) c=i; remove(c); for(int i=D[c];i!=c;i=D[i]) { ans[d]=row[i]; for(int j=R[i];j!=i;j=R[j]) remove(col[j]); if(Dance(d+1)) return 1; for(int j=L[i];j!=i;j=L[j]) resume(col[j]); } resume(c); return 0; } void display() { for(int i=R[0];i!=0;i=R[i]) { cout<<i<<' '; for(int j=D[i];j!=i;j=D[j]) cout<<'('<<j<<','<<(row[j]-1)%9+1<<')'<<' '; cout<<endl; } } }; DLX dlx; int s[100]; void getchange(int &r,int &c1,int &c2,int &c3,int &c4,int i,int j,int k) { r=(i*9+j)*9+k; c1=i*9+j+1; c2=i*9+k+81; c3=j*9+k+162; c4=map1[i][j]*9+k+243; } void slove() { int r,c1,c2,c3,c4; dlx.init(729,324); for(int i=0;i<9;++i) for(int j=0;j<9;++j) for(int k=1;k<=9;++k) if(s[i*9+j]==0 || s[i*9+j]==k) { getchange(r,c1,c2,c3,c4,i,j,k); dlx.Link(r,c1); dlx.Link(r,c2); dlx.Link(r,c3); dlx.Link(r,c4); } /* for(int i=1;i<=81;++i) for(int j=1;j<=9;++j) dlx.Link(j+(i-1)*9,i); for(int i=1;i<=81;++i) for(int j=1;j<=9;++j) dlx.Link(9*(j-1)+(i-1)%9+1+81*((i-1)/9),i+81); for(int i=1;i<=81;++i) for(int j=1;j<=9;++j) dlx.Link((j-1)*81+i,i+162); for(int i=1;i<=3;++i) for(int j=1;j<=3;++j) for(int k=1;k<=9;++k) for(int l=1;l<=3;++l) for(int m=1;m<=3;++m) dlx.Link((i-1)*243+(j-1)*27+k+(l-1)*81+(m-1)*9,(i-1)*27+(j-1)*9+k+243); for(int i=0;i<81;++i) if(s[i]!='.') { dlx.ans1[i+1]=s[i]-'0'; dlx.remove(i+1); for(int j=dlx.D[i+1];j!=i+1;j=dlx.D[j]) { if((dlx.row[j]-1)%9+1==s[i]-'0') { for(int k=dlx.R[j];k!=j;k=dlx.R[k]) dlx.remove(dlx.col[k]); break; } } } */ dlx.Dance(0); int temp=dlx.ansnum; if(temp==0) cout<<"No solution"<<endl; else if(temp==2) cout<<"Multiple Solutions"<<endl; else dlx.showans(); } const int step[4][2]={{-1,0},{0,1},{1,0},{0,-1}}; int kcou; int lu[10][10][4]; void bfs(int num,int x,int y) { queue <int> que; int temp,t1,t2; que.push(x*10+y); map1[x][y]=num; while(!que.empty()) { temp=que.front(); que.pop(); t1=temp/10; t2=temp%10; for(int k=0;k<4;++k) if(lu[t1][t2][k] && map1[t1+step[k][0]][t2+step[k][1]]==-1) { que.push((t1+step[k][0])*10+t2+step[k][1]); map1[t1+step[k][0]][t2+step[k][1]]=num; } } } void getmap() { int cou=0; for(int i=0;i<9;++i) for(int j=0;j<9;++j) if(map1[i][j]==-1) bfs(cou++,i,j); } int main() { ios::sync_with_stdio(false); int T,t; int fang[4]; cin>>T; for(int cas=1;cas<=T;++cas) { memset(map1,-1,sizeof(map1)); memset(s,0,sizeof(s)); memset(lu,0,sizeof(lu)); kcou=0; for(int i=0;i<9;++i) for(int j=0;j<9;++j) { cin>>t; for(int k=0;k<4;++k) if(((t>>(4+k))&1)==0) lu[i][j][k]=1; s[i*9+j]=t&15; } getmap(); cout<<"Case "<<cas<<':'<<endl; slove(); } return 0; }
