在看这篇题解之前,您首先需要学会: 二分求解,Floyd全源最短路,Dicnic网络最大流(当然啦,神仙们写Dicnic二进制优化、HLPP预流推进更好)
回到题目,第一眼看上去,我的第一反应是最短路和贪心。但是,很快就发现这些想法根本行不通。为什么呢?简单解释一下:
最短路算法要求的是有**起点**,有**终点**,但是这道题很明显是无序的。一个牛可以前往任意的雨棚,最短路不好统计。
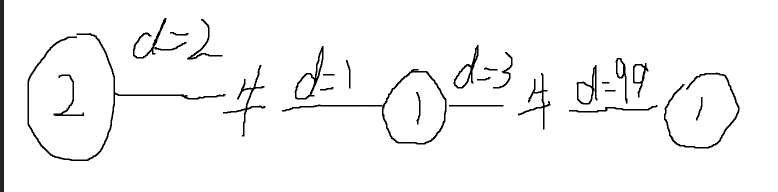
那么,贪心呢?如果我们贪心地将一头牛往最近的雨棚塞,很有可能导致别处的牛无法挤进来,从而**大幅延长**别的牛的运动时间,如下图所示。方案被否决。
(圆圈中数字代表雨棚容量,d代表距离)
既然这些算法都不好搞,不妨换个思路。
首先,无论我们的牛前往哪个雨棚,走得肯定是最短路,于是我们可以求一个全源最短路。
其次,可以想到,我们最终的答案仅取决于走得最久的那头牛,不同的走法会导致不同的结果。于是,问题又变成了“是否存在一种方案,使得最大值最小”这种东东。于是,我们选择二分时间最小值,判断所有牛是否可以在该时间内到达雨棚。
那么,如何判断答案是否合法呢?所有牛的终点不确定,因此考虑网络流建模。不妨将牛和雨棚的容量分开看,一块农田拆成两个点。从超级源点 $S$ 连向第一波点,最大流量为该点牛的数量 $x$,保证这个点有 $x$ 头牛需要安置。对于第二波点,全部连向超级汇点 $T$, 流量为雨棚的容量,即保证从这个点的雨棚“出来”的牛不超过容量。
而对于牛和雨棚,我们将合法的连上一条为 $inf$的边,保证他们无限通过。何为合法的?当然就是在同一块农田的牛和雨棚, 和最短路距离不超过当前枚举答案的点啦!(确保最长时间不能超过当前答案)。
最后,我们跑一波最大流,如果最大流等于牛的数量,证明当前的方案合法,反之,如果最大流小于牛的数量,则证明在该时间内无法保证所有的牛可以找到雨棚。
参考代码(当前弧优化的普通 $Dicnic$ 版本):
#include <bits/stdc++.h> using namespace std; #define M 100010 #define N 1010 #define ll long long const ll inf = (ll)1e18; // 一定要够大 template <class T> inline void read(T& a){ T x = 0, s = 1; char c = getchar(); while(!isdigit(c)){ if(c == '-') s = -1; c = getchar(); } while(isdigit(c)){ x = x * 10 + (c ^ '0'); c = getchar(); } a = x * s; return ; } struct node{ int v, next; ll w; public: node(int v = 0, ll w = 0, int next = -1){ // 方便初始化为 -1 this -> v = v; this -> w = w; this -> next = next; return ; } inline void clean(){ this -> v = 0; this -> w = 0; this -> next = -1; return ; } }t[M << 1]; int f[N]; ll dis[N][N]; int n, m; int suma = 0, sumb = 0; // 奶牛总数和雨棚总容量 int a[N], b[N]; int s, ht; // 起点和终点 int bian = -1; inline void add(int u, int v, ll w){ t[++bian] = node(v, w, f[u]), f[u] = bian; t[++bian] = node(u, 0, f[v]), f[v] = bian; // 反向虚边 return ; } struct Max_Flow{ // 最大流 int deth[N]; int cur[N]; bool bfs(){ queue <int> q; memset(deth, 0, sizeof(deth)); deth[s] = 1; q.push(s); while(!q.empty()){ int now = q.front(); q.pop(); for(int i = f[now]; ~i; i = t[i].next){ int v = t[i].v; if(!deth[v] && t[i].w){ deth[v] = deth[now] + 1; q.push(v); } } } return deth[ht] != 0; } ll dfs(ll now,ll dist){ if(now == ht || !dist)return dist; for(int& i = cur[now]; ~i; i = t[i].next){ ll v = t[i].v; if(deth[v] == deth[now] + 1 && t[i].w != 0){ ll di = dfs(v, min(dist, t[i].w)); if(di > 0){ t[i].w -= di; t[i^1].w += di; return di; } } } return 0; } ll Dicnic(){ ll sum = 0; while(bfs()){ memcpy(cur, f, sizeof(cur)); while(ll temp = dfs(s, inf)) sum += temp; } return sum; } } T; inline void clean(){ memset(f, -1, sizeof(f)); for(int i = 1; i <= bian; i++) t[i].clean(); bian = -1; return ; } bool judge(ll mid, int sum){ clean(); // 记得清空 for(int i = 1; i <= n; i++){ add(s, i, a[i]); add(i + n, ht, b[i]); for(int j = 1; j <= n; j++){ if(i == j || dis[i][j] <= mid) // 本身就在这块农田或者距离在当前限制之内 add(i, j + n, inf); } } return T.Dicnic() == sum; } int main(){ // freopen("hh.txt", "r", stdin); read(n), read(m); for(int i = 1; i <= n; i++){ read(a[i]), read(b[i]); suma += a[i], sumb += b[i]; // 牛的总数, 容量的总数 } if(suma > sumb){ // 特判,如果根本放不下就直接去世 printf("-1"); return 0; } s = n * 2 + 1, ht = n * 2 + 2; memset(dis, 0x3f, sizeof(dis)); for(int i = 1; i <= m; i++){ ll x, y, w; read(x), read(y), read(w); dis[x][y] = dis[y][x] = min(dis[x][y], w); } for(int k = 1; k <= n; k++) // Floyd 最短路 for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]); ll l = 0, r = 0; ll ans = -1; for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) if(i != j) r = max(r, dis[i][j]); while(l <= r){ // 二分答案 ll mid = l + r >> 1; if(judge(mid, suma)) ans = mid, r = mid - 1; else l = mid + 1; } printf("%lld ", ans < inf ? ans : -1); return 0; }