题目描述
$ASDFZ$的机房中不仅有红太阳,还有蓝太阳和原谅色太阳。
有一天,太阳们来到机房,发现桌上有不知道哪个蒟蒻放上的问题:
令$F(A,B)$表示选择一个串$A$的非空前缀$S$和串$B$的非空后缀$T$使得将串$S$和串$T$拼起来之后是回文串的方案数。
现在给定两个串$A$和$B$,令$A_i$表示串$A$的第$i$长的后缀,$B_i$为串$B$的第$i$长的前缀。
有$Q$组询问,第$i$组询问给定$x_i$和$y_i$,对每组询问求$F(A_{x_i},B_{y_i})$的值。
太阳们非常强,自然不会把时间花在这种水题上。快来做做这个题呀。
输入格式
第一行一个字符串$str$,表示数据类型。
接下来的两行分别表示字符串$A$和$B$。
接下来一行一个正整数$Q$,表示询问的个数。
接下来$Q$行,每行两个正整数$x_i$和$y_i$。
输出格式
输出$Q$行,每行一个整数,表示这一组询问的答案。
样例
样例输入:
B
newionyzz
wyxioiwen
1
1 1
样例输出:
16
数据范围与提示
样例解释:
一共有以下$16$种方案:
${S=n,T=n};{S=n,T=en};{S=ne,T=n};{S=ne,T=en};{S=ne,T=wen};{S=new,T=en};{S=new,T=wen};{S=new,T=iwen};{S=new,T=ioiwen};{S=newi,T=wen};{S=newi,T=iwen};{S=newi,T=oiwen};{S=newio,T=iwen};{S=newio,T=oiwen};{S=newio,T=ioiwen};{S=newion,T=oiwen};$
数据范围:
对于$100\%$的数据,字符串中只出现小写字母。
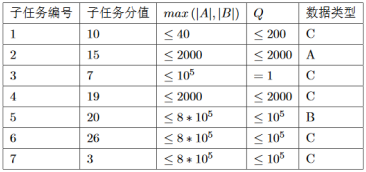
数据类型:$A:$随机数据,$B:$串$A$随机生成且$|B|leqslant {10}^4$,$C:$无特殊性质。
题解
使用二分$+hash$判断以每个位置为中心延伸出去的回文串长度,这样会对一个区间的起点或终点的回文串个数产生$1$的贡献,差分一下最后前缀和一遍即可。
对于询问,注意到每次询问只要求一个区间内的$f$和$g$的和,前缀和即可。
每次通过二分$+hash$求$LCP$,得到最长的$l$。
时间复杂度:$Theta((max(|A|,|B|)+Q)log(max(|A|,|B|)))$。
最后$3$分显然是出题人想卡你自然溢出$hash$,所以就不要挣扎了。
代码时刻
#include<bits/stdc++.h>
using namespace std;
char A[800001],B[800001];
int q;
int lenA,lenB;
long long flag[800001],pre_A[800001],suc_A[800001],pre_B[800001],suc_B[800001],f[800001],g[800001],F[800001],G[800001];
void pre_work()
{
flag[0]=1;
for(int i=1;i<=800000;i++)
flag[i]=flag[i-1]*13131%1000000007;
for(int i=1;i<=lenA;i++)
{
pre_A[i]=(pre_A[i-1]*13131%1000000007+A[i]-'a'+1)%1000000007;
suc_A[i]=(suc_A[i-1]*13131%1000000007+A[lenA-i+1]-'a'+1)%1000000007;
}
for(int i=1;i<=lenB>>1;i++)B[i]^=B[lenB-i+1]^=B[i]^=B[lenB-i+1];
for(int i=1;i<=lenB;i++)
{
pre_B[i]=(pre_B[i-1]*13131%1000000007+B[i]-'a'+1)%1000000007;
suc_B[i]=(suc_B[i-1]*13131%1000000007+B[lenB-i+1]-'a'+1)%1000000007;
}
}
int preA(int L,int R){return(pre_A[R]-pre_A[L-1]*flag[R-L+1]%1000000007+1000000007)%1000000007;}
int sucA(int L,int R){return(suc_A[R]-suc_A[L-1]*flag[R-L+1]%1000000007+1000000007)%1000000007;}
int preB(int L,int R){return(pre_B[R]-pre_B[L-1]*flag[R-L+1]%1000000007+1000000007)%1000000007;}
int sucB(int L,int R){return(suc_B[R]-suc_B[L-1]*flag[R-L+1]%1000000007+1000000007)%1000000007;}
bool checkA(int L,int R)
{
if(L<1||R>lenA)return 0;
return preA(L,R)==sucA(lenA-R+1,lenA-L+1);
}
bool checkB(int L,int R)
{
if(L<1||R>lenB)return 0;
return preB(L,R)==sucB(lenB-R+1,lenB-L+1);
}
int find_A(int L,int R)
{
int lft=1,rht=lenA;
while(lft<rht-1)
{
int mid=(lft+rht)>>1;
if(checkA(L-mid+1,R+mid-1))lft=mid;
else rht=mid;
}
if(checkA(L-rht+1,R+rht-1))return L-rht+1;
return L-lft+1;
}
int find_B(int L,int R)
{
int lft=1,rht=lenB;
while(lft<rht-1)
{
int mid=(lft+rht)>>1;
if(checkB(L-mid+1,R+mid-1))lft=mid;
else rht=mid;
}
if(checkB(L-rht+1,R+rht-1))return L-rht+1;
return L-lft+1;
}
void pre_do_A()
{
for(int i=1;i<=lenA;i++)
{
f[find_A(i,i)]++;
f[i+1]--;
if(A[i]==A[i+1])
{
f[find_A(i,i+1)]++;
f[i+1]--;
}
}
for(int i=1;i<=lenA+1;i++)
{
f[i]+=f[i-1];
F[i]=F[i-1]+f[i];
}
}
void pre_do_B()
{
for(int i=1;i<=lenB;i++)
{
g[find_B(i,i)]++;
g[i+1]--;
if(B[i]==B[i+1])
{
g[find_B(i,i+1)]++;
g[i+1]--;
}
}
for(int i=1;i<=lenB+1;i++)
{
g[i]+=g[i-1];
G[i]=G[i-1]+g[i];
}
}
int LCP(int L,int R)
{
int lft=0,rht=min(lenA-L+1,lenB-R+1);
while(lft<rht-1)
{
int mid=(lft+rht)>>1;
if(preA(L,L+mid-1)==preB(R,R+mid-1))lft=mid;
else rht=mid;
}
if(preA(L,L+rht-1)==preB(R,R+rht-1))return rht;
return lft;
}
int main()
{
scanf("%s%s%s%d",A,A+1,B+1,&q);
lenA=strlen(A+1),lenB=strlen(B+1);
pre_work();
pre_do_A();
pre_do_B();
while(q--)
{
int x,y;
scanf("%d%d",&x,&y);
int len=LCP(x,y);
printf("%lld
",F[x+len]-F[x]+G[y+len]-G[y]+len);
}
return 0;
}
rp++