HDU 5358 First One 求和（序列求和，优化）

题意：给定一个含n个元素的序列，求下式子的结果。S(i,j)表示为seq[i...j]之和。注：对于log₂⁰可视为1。数据量n<=10⁵。

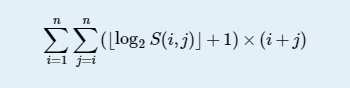
思路：即使能够在O(1)的时间内求得任意S，也是需要O(n*n)来求和的。

　　对于这种题，一般就是研究式子，看有什么办法可以减少复杂度。

　　看到式子中的向下取整符号了吗？很多数的取整结果是相同的，即使给个2147483647取整也只是30多而已（噗，忘了多少）。

　　而对于这个式子，S最大也不会超过longlong，确切计算，小于2³⁴。那么取log之后的范围这么小，如果能够知道分别有多少个的话，那就快多了。可以看得出对于同一个i，取log后的结果是呈线性的，从1到34逐步递增的（当然有可能没有那么大/小）。

　　那很好办，对于每个i，只需要将一整段“取log后向下取整的结果加1”为k的给截出来，统计k个（i,j）之和再乘以k不就是这一段的答案了吗？那么对于每个i，最多可能被截成34段啦。相比而言快了许多。复杂度为O(34*n)。

　　但是本题连这样的复杂度还是不行，还能继续优化，设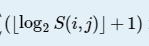为k。

　　（1）先穷举k，k=[1,34].

　　（2）再穷举i。对于每个i，假设i-1中(i-1, R)这一段的结果为k，而i中答案为k的对应段必定大于等于这段（为什么？小学老师教的序列求和技术）。所以只需从上次穷举完之处继续往后判断即可，因为i比i-1少了个数字，说不定就变小了许多，再加几个不就补回来啦！

　　再具体的话就很难说清了，看代码注释吧。我看得懂相信你也可以。

#include <bits/stdc++.h>
#define INF 0x7f7f7f7f
#define pii pair<int,int>
#define LL long long
using namespace std;
const int N=100100;
LL sum[N], up[50];
int cur[N];
void pre_cal()
{
    sum[0]=0;
    for(int i=0; i<40; i++)    up[i]= (LL)1<<i;
}
LL cal(int n)
{
    for(int i=0; i<=n; i++) cur[i]=i;   //记录以i为下标的，穷举到那里了。

    LL ans=0;
    int L=1, R=1;
    for(int k=0; k<35; k++)
    {
        R=cur[1];
        for(int i=1; i<=n; i++) //以i为下标的
        {
            L=cur[i];
            R=max(cur[i], cur[i-1]);     //这一步决定了AC或者TLE
            if(L>n) continue;            //以i为下标的已经计算完毕。

            while( R<=n &&  sum[R]-sum[i-1]<up[k] )    R++;     //找到（logx+1）为k的一段[L,R)
            if(L<R)
            {
                cur[i]=R;
                if((R-L)&1)          ans+=( (LL)(R-L)*i + (LL)(R-1+L)/2*(R-L) )*max(1,k);   //注意这里千万要转longlong
                else                 ans+=( (LL)(R-L)*i + (LL)(R-1+L)*(R-L)/2 )*max(1,k);
            }
        }
    }

    return ans;
}

int main()
{
    freopen("input.txt", "r", stdin);
    pre_cal();
    int t, n;
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d", &n);
        for(int i=1; i<=n; i++)
        {
            scanf("%lld", &sum[i]);
            sum[i] += sum[i-1];
        }
        printf("%lld
", cal(n));
    }
    return 0;
}