NFA 确定化为 DFA
子集法:
f(q,a)={q1,q2,…,qn},状态集的子集
将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合。
步骤:
1.根据NFA构造DFA状态转换矩阵
①确定DFA初态(NFA的所有初态集),字母表
②从初态出发,经字母表到达的状态集看成一个新状态
③将新状态添加到DFA状态集
④重复23步骤,直到没有新的DFA状态
2.画出DFA
3.看NFA和DFA识别的符号串是否一致。
练习:
1.解决多值映射:子集法
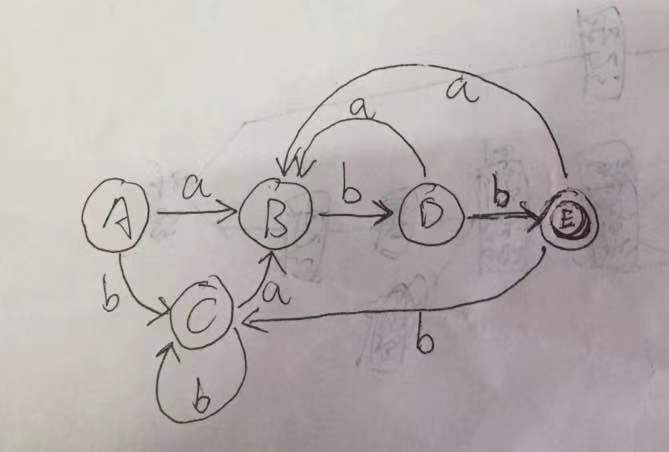
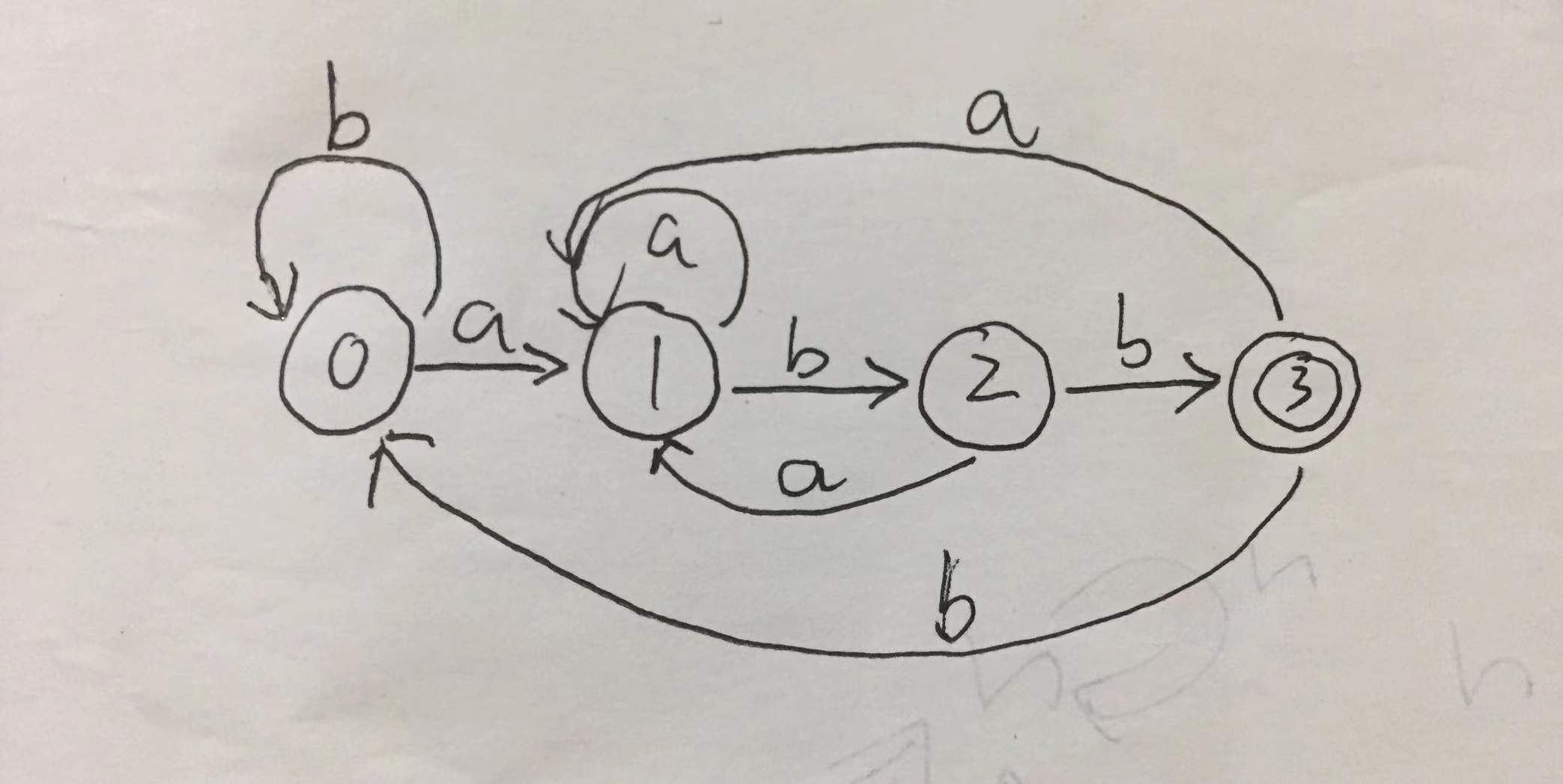
1). 发给大家的图1
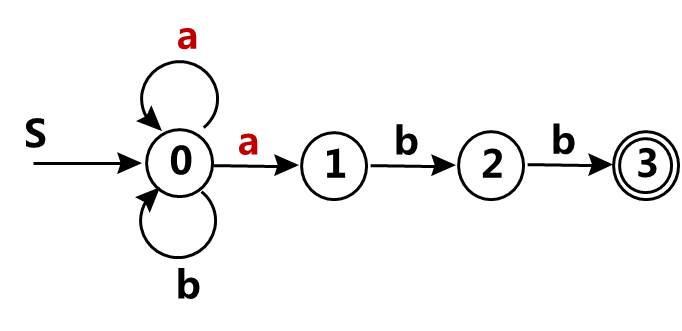
| 新状态 | a | b | |
| 0 | 0 | {0,1} | 0 |
| 1 | {0,1} | {0,1} | {0,2} |
| 2 | {0,2} | {0,1} | {0,3} |
| 3 | {0,3} | {0,1} | 0 |
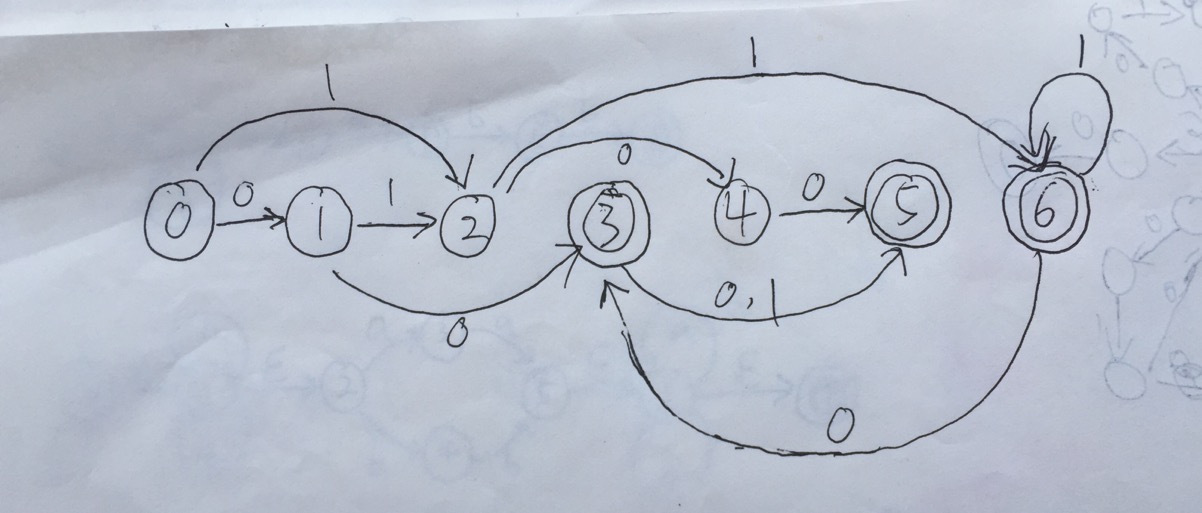
2). P64页练习3
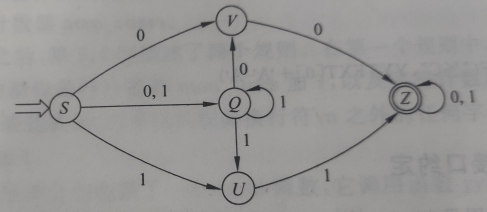
| 新状态 | 0 | 1 | |
| 0 | S | {V,Q} | {Q,U} |
| 1 | {V,Q} | {V,Z} | {Q,U} |
| 2 | {Q,U} | V | {Q,U,Z} |
| 3 | {V,Z} | Z | Z |
| 4 | V | Z | |
| 5 | Z | Z | Z |
| 6 | {Q,U,Z} | {V,Z} | {Q,U,Z} |
2.解决空弧:对初态和所有新状态求ε-闭包
1). 发给大家的图2
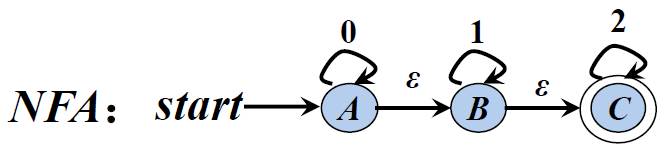
| 新状态 | 0 | 1 | 2 | |
| 0 | ε{A}={A,B,C} | ε{A}={A,B,C} | ε{B}={B,C} | ε{C}={C} |
| 1 | ε{B}={B,C} | ε{B}={B,C} | ε{C}={C} | |
| 2 | ε{C}={C} | ε{C}={C} |
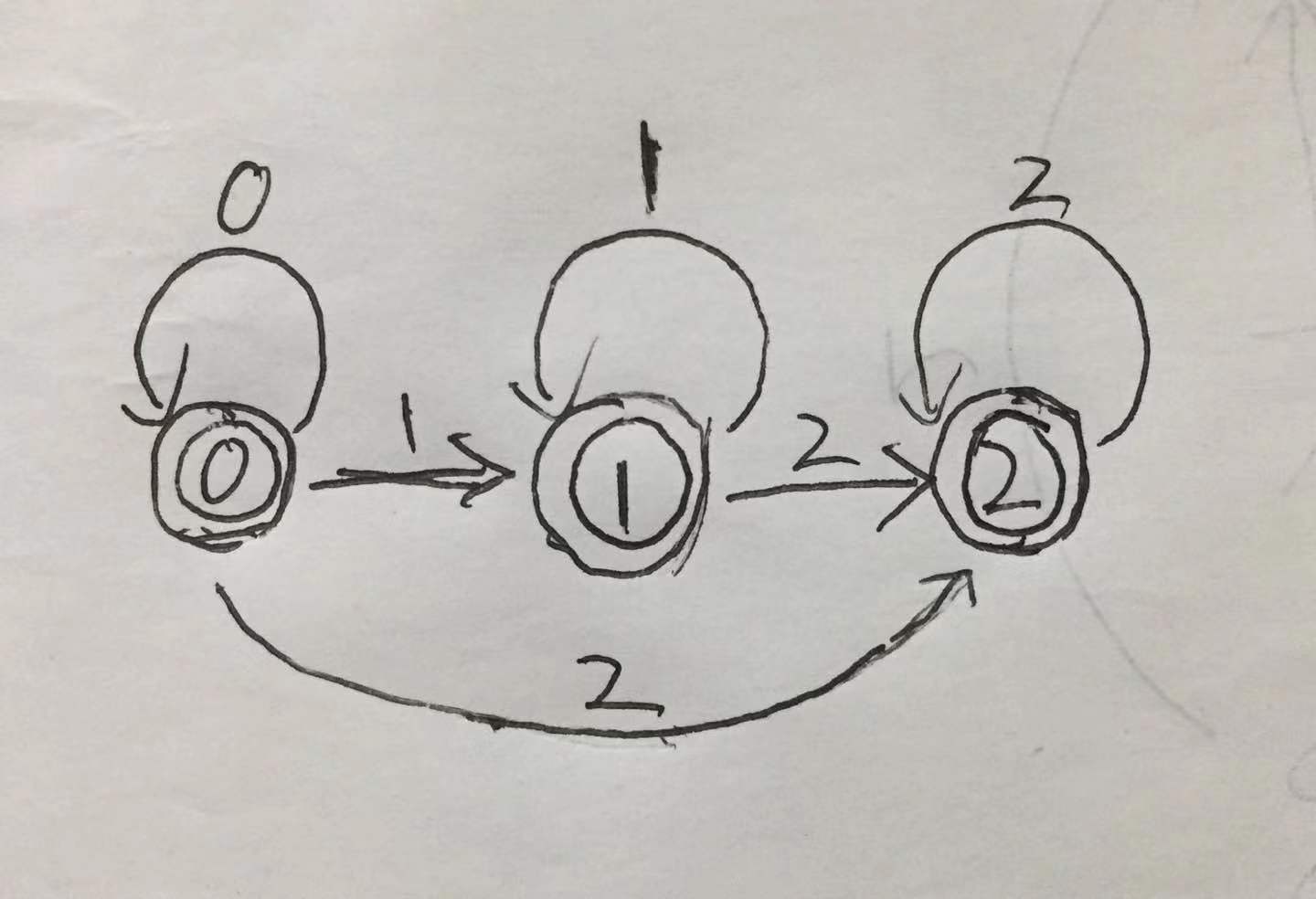
2).P50图3.6

| 新状态 | a | b | |
| A | ε{0}={01247} | ε{38}={124678} | ε{5}={124567} |
| B | ε{38}={124678} | ε{38}={124678} | ε{59}={1245679} |
| C | ε{5}={124567} | ε{38}={124678} | ε{5}={124567} |
| D | ε{59}={1245679} | ε{38}={124678} | ε{5,10}={124567 10} |
| E | ε{5,10}={124567 10} | ε{38}={124678} | ε{5}={124567} |