前端学数据结构之集合

前面的话

　　本文将详细介绍集合，这是一种不允许值重复的顺序数据结构

数据结构

　　集合是由一组无序且唯一（即不能重复）的项组成的。这个数据结构使用了与有限集合相同的数学概念，但应用在计算机科学的数据结构中。

　　在深入学习集合的计算机科学实现之前，我们先看看它的数学概念。在数学中，集合是一组不同的对象（的集）。比如说，一个由大于或等于0的整数组成的自然数集合：N={0,1,2,3,4,5,6,…}。集合中的对象列表用“{}”（大括号）包围。

　　还有一个概念叫空集。空集就是不包含任何元素的集合。比如24和29之间的素数集合。由于24和29之间没有素数（除了1和自身，没有其他正因数的大于1的自然数），这个集合就是空集。空集用“{}”表示

　　也可以把集合想象成一个既没有重复元素，也没有顺序概念的数组。在数学中，集合也有并集、交集、差集等基本操作。下面将介绍这些操作

创建集合

　　下面要实现的类就是以ECMAScript6中Set类的实现为基础的。

　　以下是Set类的骨架：

function Set() { 
  var items = {};
}

　　有一个非常重要的细节，我们使用对象而不是数组来表示集合（items）。但也可以用数组实现。 同时，JavaScript的对象不允许一个键指向两个不同的属性，也保证了集合里的元素都是唯一的

　　接下来，需要声明一些集合可用的方法（我们会尝试模拟与ECMAScript 6实现相同的Set类）

add(value)：向集合添加一个新的项。
remove(value)：从集合移除一个值。
has(value)：如果值在集合中，返回true，否则返回false。
clear()：移除集合中的所有项。
size()：返回集合所包含元素的数量。与数组的length属性类似。
values()：返回一个包含集合中所有值的数组。

【has】

　　首先要实现的是has(value)方法。这是因为它会被add、remove等其他方法调用。

　　既然我们使用对象来存储集合的值，就可以用JavaScript的in操作符来验证给定的值是否是items对象的属性

　　下面看看它的实现：

this.has = function(value){ 
  return value in items;
};

　　但这个方法还有更好的实现方式，所有JavaScript对象都有hasOwnProperty方法。这个方法返回一个表明对象是否具有特定属性的布尔值。代码如下：

this.has = function(value){
  return items.hasOwnProperty(value);
};

【add】

　　接下来要实现add方法：

this.add = function(value){ 
  if (!this.has(value)){
    items[value] = value; //{1} 
    return true;
  }
  return false;
};

　　对于给定的value，可以检查它是否存在于集合中。如果不存在，就把value添加到集合中（行{1}），返回true，表示添加了这个值。如果集合中已经有这个值，就返回false，表示没有添加它。

　　[注意]添加一个值的时候，把它同时作为键和值保存，因为这样有利于查找这个值

【remove】

　　在remove方法中，我们会验证给定的value是否存在于集合中。如果存在，就从集合中移除value（行{2}），返回true，表示值被移除；否则返回false。

　　下面来实现remove方法：

this.remove = function(value){ 
  if (this.has(value)){
    delete items[value]; //{2}
    return true;
  }
  return false;
};

　　既然用对象来存储集合的items对象，就可以简单地使用delete操作符从items对象中移除属性（行{2}）

　　使用Set类的示例代码如下：

var set = new Set(); 
set.add(1);
set.add(2);

　　在执行以上代码之后，在控制台（console.log）输出items 变量，Chrome就会输出如下内容：

 Object {1: 1, 2: 2}

　　可以看到，这是一个有两个属性的对象。属性名就是添加到集合的值，同时它也是属性值

【clear】

　　如果想移除集合中的所有值，可以用clear方法：

　　要重置items对象，需要做的只是把一个空对象重新赋值给它（行{3}）。我们也可以迭代集合，用remove方法依次移除所有的值，但既然有更简单的方法，那样做就太麻烦了

this.clear = function(){ 
  items = {}; // {3}
};

【size】

　　size方法（返回集合中有多少项）方法有三种实现方式。 第一种方法是使用一个length变量，每当使用add或remove方法时控制它；第二种方法，使用JavaScript内建的Object类的一个内建函数（ECMAScript 5以上版本）：

　　JavaScript的Object类有一个keys方法，它返回一个包含给定对象所有属性的数组。在这种情况下，可以使用这个数组的length属性（行{4}）来返回items对象的属性个数。以下代码只能在现代浏览器中运行

this.size = function(){
  return Object.keys(items).length; //{4}
};

　　第三种方法是手动提取items对象的每一个属性，记录属性的个数并返回这个数字。这个方法可以在任何浏览器上运行，和之前的代码是等价的：

　　遍历items对象的所有属性（行{5}），检查它们是否是对象自身的属性（避免重复计数—— 行{6}）。如果是，就递增count变量的值（行{7}），最后在方法结束时返回这个数字

　　[注意]不能简单地使用for-in语句遍历items对象的属性，递增count变量的值。 还需要使用has方法（以验证items对象具有该属性），因为对象的原型包含了额外的属性（属性既有继承自JavaScript的Object类的，也有属于对象自身，未用于数据结构的）

this.sizeLegacy = function(){ 
  var count = 0;
  for(var prop in items) { //{5}
    if(items.hasOwnProperty(prop)) //{6}
    ++count; //{7}
  }
  return count;
};

【values】

　　values方法也应用了相同的逻辑，提取items对象的所有属性，以数组的形式返回：

this.values = function(){
 let values = [];
 for (let i=0, keys=Object.keys(items); i<keys.length; i++) {
  values.push(items[keys[i]]);
 }
 return values;
};

　　以上代码只能在现代浏览器中运行

　　如果想让代码在任何浏览器中都能执行，可以用与之前代码等价的下面这段代码：

this.valuesLegacy = function(){
 let values = [];
 for(let key in items) { //{7}
  if(items.hasOwnProperty(key)) { //{8}
    values.push(items[key]);
  }
 }
 return values;
};

　　所以，首先遍历items对象的所有属性（行{7}），把它们添加一个数组中（行{8}），并返回这个数组。该方法类似于sizeLegacy方法，但我们添加一个数组，而不是计算属性个数

【使用Set类】

　　数据结构已经完成了，下面来试着执行一些命令，测试我们的Set类：

var set = new Set(); 
set.add(1);
console.log(set.values()); //输出["1"]
console.log(set.has(1)); //输出true
console.log(set.size()); //输出1
set.add(2);
console.log(set.values()); //输出["1", "2"]
console.log(set.has(2)); //true 
console.log(set.size()); //2
set.remove(1); 
console.log(set.values()); //输出["2"]
set.remove(2); 
console.log(set.values()); //输出[]

　　现在我们有了一个和ECMAScript6中非常类似的Set类实现

集合操作

　　对集合可以进行如下操作

　　1、并集：对于给定的两个集合，返回一个包含两个集合中所有元素的新集合

　　2、交集：对于给定的两个集合，返回一个包含两个集合中共有元素的新集合

　　3、差集：对于给定的两个集合，返回一个包含所有存在于第一个集合且不存在于第二个集合的元素的新集合

　　4、子集：验证一个给定集合是否是另一集合的子集

【并集】

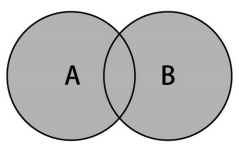
　　并集的数学概念是集合A和B的并集，表示为A∪B，定义如下：

A∪B = { x | x ∈ A∨x ∈ B }

　　意思是x（元素）存在于A中，或x存在于B中。下图展示了并集操作：

　　现在来实现Set类的union方法：

　　首先需要创建一个新的集合，代表两个集合的并集（行{1}）。接下来，获取第一个集合（当前的Set类实例）所有的值（values），遍历并全部添加到代表并集的集合中（行{2}）。然后对第二个集合做同样的事（行{3}）。最后返回结果

this.union = function(otherSet){
 let unionSet = new Set(); //{1}
 let values = this.values(); //{2}
 for (let i=0; i<values.length; i++){
  unionSet.add(values[i]);
 }
 values = otherSet.values(); //{3}
 for (let i=0; i<values.length; i++){
   unionSet.add(values[i]);
 }
 return unionSet;
};

　　测试一下上面的代码：

var setA = new Set(); 
setA.add(1);
setA.add(2);
setA.add(3);

var setB = new Set();
setB.add(3);
setB.add(4);
setB.add(5);
setB.add(6);

var unionAB = setA.union(setB);
console.log(unionAB.values());

　　输出为["1", "2", "3", "4", "5", "6"]。注意元素3同时存在于A和B中，它在结果的 集合中只出现一次

【交集】

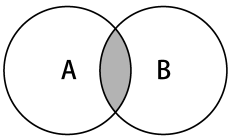
　　交集的数学概念是集合A和B的交集，表示为A∩B，定义如下：

A∩B = { x | x ∈ A∧x ∈ B }

　　意思是x（元素）存在于A中，且x存在于B中。下图展示了交集操作：

　　现在来实现Set类的intersection方法：

　　intersection方法需要找到当前Set实例中，所有存在于给定Set实例中的元素。首先创建一个新的Set实例，这样就能用它返回共有的元素（行{1}）。接下来，遍历当前Set实例所有的值（行{2}），验证它们是否也存在于otherSet实例（行{3}）。可以用前面实现的has方法来验证元素是否存在于Set实例中。然后，如果这个值也存在于另一个Set实例中，就将其添加到创建的intersectionSet变量中（行{4}），最后返回它。

this.intersection = function(otherSet){
 let intersectionSet = new Set(); //{1}
 let values = this.values();
 for (let i=0; i<values.length; i++){ //{2}
  if (otherSet.has(values[i])){ //{3}
    intersectionSet.add(values[i]); //{4}
  }
 }
 return intersectionSet;
}

　　测试一下上面的代码：

var setA = new Set(); 
setA.add(1);
setA.add(2);
setA.add(3);

var setB = new Set(); 
setB.add(2);
setB.add(3);
setB.add(4);

var intersectionAB = setA.intersection(setB); 
console.log(intersectionAB.values());

　　输出为["2", "3"]，因为2和3同时存在于两个集合中

【差集】

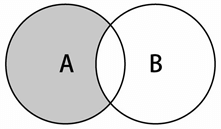
　　差集的数学概念，集合A和B的差集，表示为A-B，定义如下：

　　意思是x（元素）存在于A中，且x不存在于B中。下图展示了集合A和B的差集操作：

　　现在来实现Set类的difference方法：

　　intersection方法会得到所有同时存在于两个集合中的值。而difference方法会得到所有存在于集合A但不存在于B的值。因此这两个方法在实现上唯一的区别就是行{3}。只获取不存在于otherSet实例中的值，而不是也存在于其中的值。行{1}、{2}和{4}是完全相同的

this.intersection = function(otherSet){
 let intersectionSet = new Set(); //{1}
 let values = this.values();
 for (let i=0; i<values.length; i++){ //{2}
  if (!otherSet.has(values[i])){ //{3}
    intersectionSet.add(values[i]); //{4}
  }
 }
 return intersectionSet;
}

　　测试一下上面的代码：

var setA = new Set(); 
setA.add(1);
setA.add(2);
setA.add(3);

var setB = new Set(); 
setB.add(2);
setB.add(3);
setB.add(4);

var differenceAB = setA.difference(setB); 
console.log(differenceAB.values());

　　输出为["1"]，因为1是唯一一个仅存在于setA的元素

【子集】

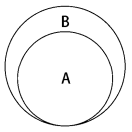
　　子集的数学概念是集合A是B的子集（或集合B包含了A），表示为A⊆B，定义如下：

∀x { x ∈ A → x ∈ B }

　　意思是集合A中的每一个x（元素），也需要存在于B中。下图展示了集合A是集合B的子集：

　　现在来实现Set类的subset方法：

　　首先需要验证的是当前Set实例的大小。如果当前实例中的元素比otherSet实例更多，它就不是一个子集（行{1}）。子集的元素个数需要小于或等于要比较的集合。

　　接下来要遍历集合中的所有元素（行{2}），验证这些元素也存在于otherSet中（行{3}）。如果有任何元素不存在于otherSet中，就意味着它不是一个子集，返回false（行{4}）。如果所有元素都存在于otherSet中，行{4}就不会被执行，那么就返回true（行{5}）。

this.subset = function(otherSet){
 if (this.size() > otherSet.size()){ //{1}
  return false;
 } else {
  let values = this.values();
  for (let i=0; i<values.length; i++){ //{2}
    if (!otherSet.has(values[i])){ //{3}
      return false; //{4}
    }
  }
  return true; //{5}
 }
};

　　检验一下上面的代码效果如何：

var setA = new Set(); 
setA.add(1);
setA.add(2);

var setB = new Set(); 
setB.add(1);
setB.add(2);
setB.add(3);

var setC = new Set(); 
setC.add(2);
setC.add(3);
setC.add(4);

console.log(setA.subset(setB)); 
console.log(setA.subset(setC));

　　我们有三个集合：setA是setB的子集（因此输出为true），然而setA不是setC的子集（setC 只包含了setA中的2，而不包含1），因此输出为false

【完整代码】

　　关于集合的完整代码如下

function Set() {

    let items = {};

    this.add = function(value){
        if (!this.has(value)){
            items[value] = value;
            return true;
        }
        return false;
    };

    this.delete = function(value){
        if (this.has(value)){
            delete items[value];
            return true;
        }
        return false;
    };

    this.has = function(value){
        return items.hasOwnProperty(value);
        //return value in items;
    };

    this.clear = function(){
        items = {};
    };

    /**
     * Modern browsers function
     * IE9+, FF4+, Chrome5+, Opera12+, Safari5+
     * @returns {Number}
     */
    this.size = function(){
        return Object.keys(items).length;
    };

    /**
     * cross browser compatibility - legacy browsers
     * for modern browsers use size function
     * @returns {number}
     */
    this.sizeLegacy = function(){
        let count = 0;
        for(let key in items) {
            if(items.hasOwnProperty(key))
                ++count;
        }
        return count;
    };

    /**
     * Modern browsers function
     * IE9+, FF4+, Chrome5+, Opera12+, Safari5+
     * @returns {Array}
     */
    this.values = function(){
        let values = [];
        for (let i=0, keys=Object.keys(items); i<keys.length; i++) {
            values.push(items[keys[i]]);
        }
        return values;
    };

    this.valuesLegacy = function(){
        let values = [];
        for(let key in items) {
            if(items.hasOwnProperty(key)) {
                values.push(items[key]);
            }
        }
        return values;
    };

    this.getItems = function(){
      return items;
    };

    this.union = function(otherSet){
        let unionSet = new Set(); //{1}

        let values = this.values(); //{2}
        for (let i=0; i<values.length; i++){
            unionSet.add(values[i]);
        }

        values = otherSet.values(); //{3}
        for (let i=0; i<values.length; i++){
            unionSet.add(values[i]);
        }

        return unionSet;
    };

    this.intersection = function(otherSet){
        let intersectionSet = new Set(); //{1}

        let values = this.values();
        for (let i=0; i<values.length; i++){ //{2}
            if (otherSet.has(values[i])){    //{3}
                intersectionSet.add(values[i]); //{4}
            }
        }

        return intersectionSet;
    };

    this.difference = function(otherSet){
        let differenceSet = new Set(); //{1}

        let values = this.values();
        for (let i=0; i<values.length; i++){ //{2}
            if (!otherSet.has(values[i])){    //{3}
                differenceSet.add(values[i]); //{4}
            }
        }

        return differenceSet;
    };

    this.subset = function(otherSet){

        if (this.size() > otherSet.size()){ //{1}
            return false;
        } else {
            let values = this.values();
            for (let i=0; i<values.length; i++){ //{2}
                if (!otherSet.has(values[i])){    //{3}
                    return false; //{4}
                }
            }
            return true;
        }
    };
}

【ES6】

　　ES6版本的代码如下

let Set2 = (function () {

    const items = new WeakMap();

    class Set2 {

        constructor () {
            items.set(this, {});
        }

        add(value){
            if (!this.has(value)){
                let items_ = items.get(this);
                items_[value] = value;
                return true;
            }
            return false;
        }

        delete(value){
            if (this.has(value)){
                let items_ = items.get(this);
                delete items_[value];
                return true;
            }
            return false;
        }

        has(value){
            let items_ = items.get(this);
            return items_.hasOwnProperty(value);
        }

        clear(){
            items.set(this, {});
        }

        size(){
            let items_ = items.get(this);
            return Object.keys(items_).length;
        }


        values(){
            let values = [];
            let items_ = items.get(this);
            for (let i=0, keys=Object.keys(items_); i<keys.length; i++) {
                values.push(items_[keys[i]]);
            }
            return values;
        }

        getItems(){
            return items.get(this);
        }

        union(otherSet){
            let unionSet = new Set();

            let values = this.values();
            for (let i=0; i<values.length; i++){
                unionSet.add(values[i]);
            }

            values = otherSet.values();
            for (let i=0; i<values.length; i++){
                unionSet.add(values[i]);
            }

            return unionSet;
        }

        intersection(otherSet){
            let intersectionSet = new Set();

            let values = this.values();
            for (let i=0; i<values.length; i++){
                if (otherSet.has(values[i])){
                    intersectionSet.add(values[i]);
                }
            }

            return intersectionSet;
        }

        difference(otherSet){
            let differenceSet = new Set();

            let values = this.values();
            for (let i=0; i<values.length; i++){
                if (!otherSet.has(values[i])){
                    differenceSet.add(values[i]);
                }
            }

            return differenceSet;
        };

        subset(otherSet){

            if (this.size() > otherSet.size()){
                return false;
            } else {
                let values = this.values();
                for (let i=0; i<values.length; i++){
                    if (!otherSet.has(values[i])){
                        return false;
                    }
                }
                return true;
            }
        };
    }
    return Set2;
})();

ES6

　　ECMAScript 2015新增了Set类。我们可以基于ES6的Set开发我们的Set类

　　和我们的Set不同，ES6的Set的values方法返回Iterator，而不是值构成的数组。另一个区别是，我们实现的size方法返回set中存储的值的个数，而ES6的Set则有一个size属性

let set = new Set();
set.add(1);
console.log(set.values()); // 输出@Iterator
console.log(set.has(1)); // 输出true
console.log(set.size); // 输出1 

　　可以用delete方法删除set中的元素：

set.delete(1); 

　　clear方法会重置set数据结构，这跟我们实现的功能一样

【集合】

　　我们的Set类实现了并集、交集、差集、子集等数学操作，然而ES6原生的Set并没有这些功能

　　我们可以创建一个新的集合，用来添加两个集合中所有的元素（行{1}）。迭代这两个集合（行{2}、行{3}），把所有元素都添加到并集的集合中。代码如下：

let unionAb = new Set(); //{1}
for (let x of setA) unionAb.add(x); //{2}
for (let x of setB) unionAb.add(x); //{3} 

　　模拟交集操作需要创建一个辅助函数，来生成包含setA和setB都有的元素的新集合（行 {1}）。代码如下：

let intersection = function(setA, setB) {
 let intersectionSet = new Set();
 for (let x of setA) {
 　　if (setB.has(x)) { //{1}
 　　　　intersectionSet.add(x);
 　　}
 }
 return intersectionSet;
};
let intersectionAB = intersection(setA, setB); 

　　交集可以用更简单的语法实现，代码如下：

intersectionAb = new Set([x for (x of setA) if (setB.has(x))]); 

　　这和intersection函数的效果完全一样

　　交集操作创建的集合包含setA和setB都有的元素，差集操作创建的集合包含的则是setA有 而setB没有的元素。看下面的代码：

let difference = function(setA, setB) {
 let differenceSet = new Set();
 for (let x of setA) {
     if (!setB.has(x)) { //{1}
         differenceSet.add(x);
     }
 }
 return differenceSet;
};
let differenceAB = difference(setA, setB); 

　　intersection函数和difference函数只有行{1}不同，因为差集中只添加setA有而setB 没有的元素

　　差集也可以用更简单的语法实现，代码如下：

differenceAB = new Set([x for (x of setA) if (!setB.has(x))]); 

【set代码】

　　基于ES6的set开发的类的完整代码如下

let set = new Set();

//--------- Union ----------
let unionAb = new Set();
for (let x of setA) unionAb.add(x);
for (let x of setB) unionAb.add(x);

//--------- Intersection ----------
let intersection = function(setA, setB){
    let intersectionSet = new Set();

    for (let x of setA){
        if (setB.has(x)){
            intersectionSet.add(x);
        }
    }

    return intersectionSet;
};
let intersectionAB = intersection(setA, setB);
//alternative - works on FF only
//intersectionAb = new Set([x for (x of setA) if (setB.has(x))]);

//--------- Difference ----------
let difference = function(setA, setB){
    let differenceSet = new Set();

    for (let x of setA){
        if (!setB.has(x)){
            differenceSet.add(x);
        }
    }

    return differenceSet;
};
let differenceAB = difference(setA, setB);
//alternative  - works on FF only
//differenceAB = new Set([x for (x of setA) if (!setB.has(x))]);