
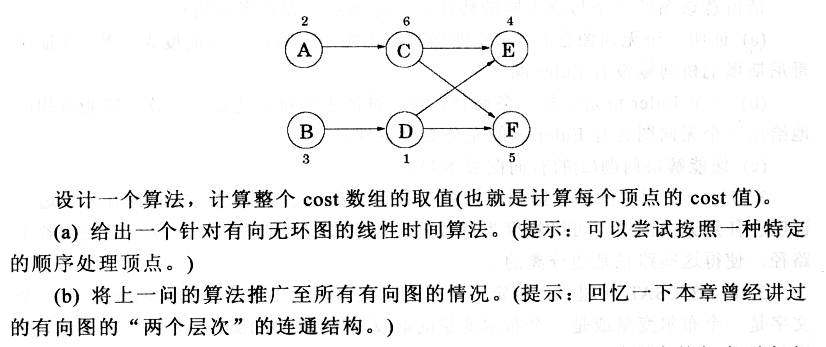
(a)首先对有向无环图进行拓扑排序,再按拓扑排序的逆序依次计算每个顶点的cost值,每个顶点的cost值为自身的price值与相邻顶点间的cost值得最小值
(b)求出图中的每一个强连通分量,并把所有得强连通分量看成是一个有向无环图,设每一个强连通分量的price值为该强连通分量中顶点的最小的price值。然后再按(a)中的步骤处理DAG

1 package org.xiu68.ch03.ex11; 2 3 import java.util.ArrayDeque; 4 import java.util.ArrayList; 5 import java.util.List; 6 import java.util.Stack; 7 8 public class Ex3_25 { 9 public static void main(String[] args) { 10 // TODO Auto-generated method stub 11 int[][] edges=new int[][]{ 12 {0,0,1,0,0,0}, 13 {0,0,0,1,0,0}, 14 {0,0,0,0,1,1}, 15 {0,0,0,0,1,1}, 16 {0,0,0,0,0,0}, 17 {0,0,0,0,0,0} 18 }; 19 int[] price=new int[]{2,3,6,1,4,5}; 20 MGraph2 m1=new MGraph2(edges, price); 21 m1.getCost(); 22 System.out.println("*****************"); 23 m1.getSccCost(); 24 //输出 25 /* 26 cost[0]:2 27 cost[1]:1 28 cost[2]:4 29 cost[3]:1 30 cost[4]:4 31 cost[5]:5 32 ***************** 33 cost[0]=2 34 cost[1]=1 35 cost[2]=4 36 cost[3]=1 37 cost[4]=4 38 cost[5]=5 39 */ 40 System.out.println("*******************"); 41 int[][] edges1=new int[][]{ 42 {0,0,0,0,0,0,0}, 43 {1,0,0,1,0,0,0}, 44 {1,0,0,1,0,0,0}, 45 {0,0,0,0,1,1,0}, 46 {0,0,0,1,0,0,1}, 47 {0,0,0,1,0,0,1}, 48 {0,0,0,0,1,1,0} 49 }; 50 int[] price1=new int[]{6,7,9,5,3,4,2}; 51 MGraph2 m2=new MGraph2(edges1, price1); 52 m2.getSccCost(); 53 //输出 54 /* 55 cost[0]=6 56 cost[1]=2 57 cost[2]=2 58 cost[3]=2 59 cost[4]=2 60 cost[5]=2 61 cost[6]=2 62 */ 63 } 64 65 } 66 67 class MGraph2{ 68 private int[][] edges; //有向图 69 private int[][] rEdges; //有向图的反向图 70 private int vexNum; //顶点数量 71 private int[] price; //每个顶点的相对价格 72 private int[][] sccEdges; //强连通分量(DAG)之间的关系 73 private Stack<Integer> stack; //存储反向图深度优先遍历的post值 74 75 public MGraph2(int[][] edges,int[] price){ 76 this.edges=edges; 77 this.vexNum=edges.length; 78 this.price=price; 79 this.stack=new Stack<>(); 80 this.rEdges=new int[vexNum][vexNum]; 81 this.sccEdges=new int[vexNum][vexNum]; 82 83 //求原图的反向图 84 for(int i=0;i<vexNum;i++){ 85 for(int j=i+1;j<vexNum;j++){ 86 rEdges[i][j]=edges[j][i]; 87 rEdges[j][i]=edges[i][j]; 88 } 89 } 90 } 91 92 //********************************************************** 93 //针对有向无环图,获取每个顶点的cost值 94 public void getCost(){ 95 ArrayDeque<Integer> queue=new ArrayDeque<Integer>(); //存取拓扑排序的逆序 96 int[] cost=new int[vexNum]; 97 for(int i=0;i<vexNum;i++) 98 cost[i]=price[i]; 99 topoSort(queue,edges,vexNum); 100 101 //依次处理每个顶点,每个顶点取自身的price值和邻接点的cost值得最小值 102 while(!queue.isEmpty()){ 103 int v=queue.poll(); 104 for(int i=0;i<vexNum;i++){ 105 if(edges[v][i]==1 && cost[i]<cost[v]) 106 cost[v]=cost[i]; 107 } 108 } 109 for(int i=0;i<vexNum;i++) 110 System.out.println("cost["+i+"]:"+cost[i]); 111 } 112 //求拓扑排序的逆序 113 public void topoSort(ArrayDeque<Integer> queue,int[][] edgeArray,int vertexNum){ 114 boolean[] visited=new boolean[vertexNum]; 115 for(int i=0;i<vertexNum;i++){ 116 if(!visited[i]) 117 topoDFS(queue,visited,edgeArray,vertexNum,i); 118 } 119 } 120 //深度优先遍历求拓扑排序 121 public void topoDFS(ArrayDeque<Integer> queue,boolean[] visited,int[][] edgeArray,int vertexNum,int v){ 122 visited[v]=true; 123 for(int i=0;i<vertexNum;i++){ 124 if(edgeArray[v][i]==1 && !visited[i]){ 125 topoDFS(queue,visited,edgeArray,vertexNum,i); 126 } 127 } 128 queue.add(v); 129 } 130 131 132 133 //**************************************************************** 134 //针对所有有向图的情况,获取每个顶点的cost值 135 public void getSccCost(){ 136 rDFSTraverse(); //先对反向图进行深度优先遍历 137 138 List<List<Integer>> sccs=new ArrayList<>(); //存放每一个强连通部件对应的顶点 139 140 boolean[] visited=new boolean[vexNum]; //记录深度优先遍历原图过程中非当前强连通分量已经访问的顶点 141 int[] visitedN=new int[vexNum]; //记录顶点属于第几个强连通分量 142 int n=0; //第几个强连通部件 143 144 for(int i=0;i<vexNum;i++){ 145 visitedN[i]=-1; 146 } 147 148 //依次出栈,并从该顶点开始对原图进行深度优先遍历,获取每个强连通分量对应的顶点 149 //并获取DAG之间的关系 150 while(!stack.isEmpty()){ 151 int v=stack.pop(); 152 if(!visited[v]){ 153 sccs.add(new ArrayList<Integer>()); 154 List<Integer> vexs=new ArrayList<>(); //获取第n个强连通分量的顶点 155 156 sccDFS(visited,visitedN,v,sccs,vexs,/*isSinkSCC,*/n); 157 //为了知道遍历第n个强连通分量之前已经访问过哪些顶点 158 //遍历完一个强连通分量再设visited值 159 for(int i=0;i<vexs.size();i++){ 160 visited[vexs.get(i)]=true; 161 } 162 n++; 163 } 164 } 165 166 167 int[] sccPrice=new int[sccs.size()]; 168 int[] sccCost=new int[sccs.size()]; 169 //将每个强连通分量的price值设为强连通分量中price值最小的顶点的price值 170 for(int i=0;i<sccs.size();i++){ 171 sccPrice[i]=Integer.MAX_VALUE; 172 for(int j=0;j<sccs.get(i).size();j++){ 173 //sccs.get(i).get(j) 第i个强连通分量的第j个顶点 174 if(price[sccs.get(i).get(j)]<sccPrice[i]){ 175 sccPrice[i]=price[sccs.get(i).get(j)]; 176 } 177 } 178 } 179 180 //对DAG进行拓扑排序 181 ArrayDeque<Integer> topoQueue=new ArrayDeque<>(); 182 topoSort(topoQueue, sccEdges, sccs.size()); 183 184 for(int i=0;i<sccs.size();i++) 185 sccCost[i]=sccPrice[i]; 186 187 //topoSort(topoQueue,edges,vexNum); 188 ////依次处理DAG中每个顶点,每个顶点取自身的price值和邻接点的cost值得最小值 189 while(!topoQueue.isEmpty()){ 190 int v=topoQueue.poll(); 191 for(int i=0;i<sccs.size();i++){ 192 if(sccEdges[v][i]==1 && sccCost[i]<sccCost[v]) 193 sccCost[v]=sccCost[i]; 194 } 195 } 196 197 //visitedN[i] 第i个顶点在第几个强连通分量中 198 for(int i=0;i<vexNum;i++) 199 System.out.println("cost["+i+"]="+sccCost[visitedN[i]]); 200 } 201 202 //对原图进行深度优先遍历 203 //在汇点强连通部件中对某个顶点进行深度优先遍历则刚好访问该强连通部件的所有顶点 204 private void sccDFS(boolean[] visited,int[] visitedN,int v,List<List<Integer>> sccs, 205 List<Integer> vexs,/*boolean[] isSinkSCC,*/int n){ 206 sccs.get(n).add(v); 207 vexs.add(v); 208 visitedN[v]=n; 209 for(int i=0;i<vexNum;i++){ 210 if(edges[v][i]==1){ 211 //若遍历到其他强连通分量的顶点说明该强连通分量不是汇点强连通分量 212 if(visited[i]){ 213 //i为其他强连通分量的顶点,所以当前强连通分量有一条边指向i所在的强连通分量 214 sccEdges[n][visitedN[i]]=1; 215 }else if(visitedN[i]!=n){ 216 sccDFS(visited,visitedN,i,sccs,vexs,/*isSinkSCC,*/n); 217 } 218 } 219 }//for 220 } 221 //*********************************************************** 222 /* 223 * 对反向图进行深度优先遍历,post值最大的顶点将位于反向图中的一个源点强连通部件, 224 * 也就是原图中的某个汇点连通部件的某个顶点 225 * 按post值从小到大,压入栈中 226 */ 227 public void rDFSTraverse(){ 228 boolean[] visited=new boolean[vexNum]; 229 for(int i=0;i<vexNum;i++){ 230 if(!visited[i]){ 231 rDFS(visited,stack,i); 232 } 233 } 234 } 235 //对反向图做深度优先遍历 236 private void rDFS(boolean[] visited,Stack<Integer> stack,int v){ 237 visited[v]=true; 238 for(int i=0;i<vexNum;i++){ 239 if(rEdges[v][i]==1 && !visited[i]){ 240 rDFS(visited,stack,i); 241 } 242 } 243 stack.push(v); 244 } 245 }
