花花的礼物 (huahua)

from dtoj 1936

题意

花花是个爱动脑子的孩子，在她的生日的时候，她的爸爸给她准备了个礼物。但是，她的爸爸并不想让她轻易得到礼物，他把礼物放在了一个箱子里面，只有输入正确的密码才能打开箱子，而她的爸爸告诉了她这个礼物该怎么得到：
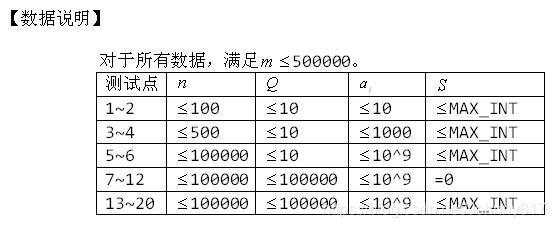
他们所在的城市可以看成有 $n$ 个点， $m$ 条边的无向图，每个点上有一个权值 $a^i$，每条边有一个权值 $w$ 。
我们定义两个点 $x$ ， $y$ 关于 $k$ 联通当且仅当存在一条从 $x$ 到 $y$ 的路径，满足这条路径上的 $w$ 的最大值小于等于 $k$ 。
而密码就是和节点 $x$ 关于 $k$ 联通的所有节点的 $a^i$ 构成的集合 $B$ 的 $summex$ 。
我们定义一个可重复数集 $B$ 的 $summex$ 为无法用 $B$ 集合的子集的和表示的正整数的最小值。
例如，$B=\{1,1,3,7\}$ ，他能表示 $0\{\}$ ， $1\{1\}$ ， $2\{1,1\}$ ， $3\{3\}$ ， $4\{1+3\}$ ， $5\{1+1+3\}$ ，但是他不能表示 $6$ ，所以 $summex\{1,1,3,7\}$ 是 $6$。
由于她的爸爸有点健忘，他可能会记错，所以会有多组（ $Q$ 组）询问。对于每组询问，你都要给一个正确的答案。
为了提高难度，我们会对数据加密，对于一个给定的数 $S$ ，解密输入中的C++代码是：

inline void decode(int &x, int &y){
	x = (lstans & S) ^ x;
	y = (lstans & S) ^ y;
}

其中的 $lstans$ 是上次询问的答案。

题解

考虑离线的做法
按照 $k$ 排序，每个点当做一棵线段树，做最小生成树的时候，把边权 $<=k$ 的边连接，并且线段树合并到根上，然后按照神秘数的做法找出 $ans$ 即可
(到时候再补神秘数的题解
考虑在线作法，把 $Kruskal$ 重构树建出，然后每个点开一棵线段树，然后往根合并上去，查询的时候倍增找到其路径上第一个点权 $<=k$ 的线段树，按照神秘数的做法即可
(注意原来的边有 $5e5$ 条(一开始别的都对了，然后被这个坑了一晚上:(
上代码

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N=2e5+5;LL s[N*20],ans;
int head[N],V[N],nex[N],b[N],B,tt;
int n,m,Q,S,a[N],tot,t,w[N],f[N];
int ls[N*20],rs[N*20],T[N],fa[N][20];
struct O{int x,y,z;}p[500005];
bool cmp(O A,O B){return A.z<B.z;}
int get(int x){
	return x==f[x]?x:f[x]=get(f[x]);
}
inline void add(int u,int v){
	V[++t]=v;nex[t]=head[u];head[u]=t;
}
#define d ((l+r)>>1)
void ins(int& x,int l,int r,int v){
	x=++tt;s[x]=v;if (l==r) return;
	if (v<=b[d]) ins(ls[x],l,d,v);
	else ins(rs[x],d+1,r,v);
}
int update(int x1,int x2){
	if (!x1 || !x2) return x1+x2;
	int x=++tt;s[x]=s[x1]+s[x2];
	ls[x]=update(ls[x1],ls[x2]);
	rs[x]=update(rs[x1],rs[x2]);
	return x;
}
LL query(int x,int l,int r,LL v){
	if (!x) return 0ll;
	if (l==r) return (LL)b[l]>v?0ll:s[x];
	if (b[d]>=v) return query(ls[x],l,d,v);
	return s[ls[x]]+query(rs[x],d+1,r,v);
}
void dfs(int x){
	for (int i=1;fa[fa[x][i-1]][i-1];i++)
		fa[x][i]=fa[fa[x][i-1]][i-1];
	for (int i=head[x];i;i=nex[i])
		fa[V[i]][0]=x,dfs(V[i]);
}
int main(){
	scanf("%d%d%d%d",&n,&m,&Q,&S);
	for (int i=1;i<=n;i++)
		scanf("%d",&a[i]),b[i]=a[i];
	sort(b+1,b+n+1);B=unique(b+1,b+n+1)-b-1;
	for (int i=1;i<=m;i++)
		scanf("%d%d%d",&p[i].x,&p[i].y,&p[i].z);
	sort(p+1,p+m+1,cmp);tot=n;
	for (int i=1;i<=n;i++) ins(T[i],1,B,a[i]);
	for (int i=1;i<n+n;i++) f[i]=i;
	for (int x,y,i=1;i<=m;i++){
		x=get(p[i].x),y=get(p[i].y);
		if (x==y) continue;
		w[++tot]=p[i].z;add(tot,x);add(tot,y);
		f[x]=tot;f[y]=tot;T[tot]=update(T[x],T[y]);
	}
	for (int i=1;i<=tot;i++) if (f[i]==i) dfs(i);
	for (int x,k;Q--;printf("%lld
",ans)){
		scanf("%d%d",&x,&k);
		x=(ans&S)^x;k=(ans&S)^k;
		for (int i=19;~i;i--)
			if (fa[x][i] && w[fa[x][i]]<=k)
				x=fa[x][i];
		ans=1;LL p;while(1){
			p=query(T[x],1,B,ans);
			if (p>=ans) ans=p+1;else break;
		}
	}
	return 0;
}