——线段树详解
第一次接触线段树大概是在2016.11,当时啥都不懂,lca啥的都不知道,通过啃博客和教材花大概一周强行理解了单点修改,区间查询的线段树(拼命调程序却调不出来的感受。。)。当然,理解了以后就觉得只要明白线段树的原理,现场15min码出来不是什么难事。
今天一时性起,打算把我理解的线段树记下来。
一、线段树是什么?
1.我们为什么要使用线段树?如果只是为了维护一个序列本身,直接用数组就行了,不必使用线段树,就好比能用线段树的时候没必要码个treap上去。线段树的核心作用是维护一个序列的信息,当然这个信息不是什么都行,必须满足区间加法(见ZKW的PPT《统计的力量》)。e.g.可以维护区间和,区间平方和,区间方差等等(都是些基础运用)。
2.线段树支持哪些操作?即便是最低级的线段树也应该支持单点修改和区间查询,或者区间修改单点查询。(如果只能单点修改单点查询还要线段树干嘛qwq)除此以外还有区间修改区间查询。
3.线段树效率的本质?基于堆存储形式确保高度是O(logn)的,因此每次操作只会影响到O(logn)个结点,同时每个节点的维护工作在O(1)时间内完成(当然高级一点的树套树不必拘泥于这点)。
二、单点修改区间查询
1.修改?简单!在线段树上找到要修改的下标对应的叶子结点,修改它的值,自下往上维护信息。
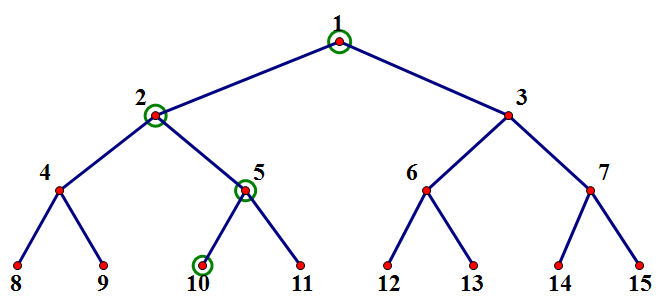
如图:假如要修改第三个位置的值,绿圈所标识的就是被更新的结点,易见复杂度与高度同阶O(logn)。
2.查询?稍微复杂一些。从直觉上讲,我们走到一个结点时,如果已经能用O(1)时间得出这个结点在要查询区间中所做出的贡献(也就是完全被包含或无交集),那么就应该返回答案了,但是这样做复杂度能扛得住吗?
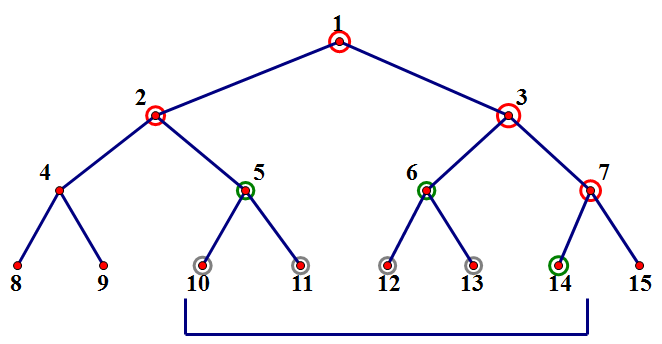
看这幅图:红色结点表示搜索过程中经过的结点,绿色结点表示搜索的末端结点,灰色结点是被忽略的结点,值得在意的事,对于每一层的被涉及的结点,可以分为两类:第一类是红色结点——它们与待查询区间有交集,但不包含,搜索到它们时会继续向下延伸到两个子结点;第二类是绿色结点——它们与待测区间是完全被包含的关系,因此搜索到这里就不继续向下了。然后由两个性质:第一个是红色结点每层至多两个,第二个是绿色结点每层至多两个。稍微想想就知道,每层的红色结点就是边上的两个(可能不到两个,但一定在边上),而相邻的3个绿色结点一定有两个可以合并为父节点,也就是上一层的绿色结点,这两个就没有存在的必要了。基于这两个性质,总共涉及到的结点数不超过4*logn个,复杂度满足O(log n)。
三、区间修改单点查询
1.修改?似乎很难,但是如果我们将”二“中的区间查询用到这里,就能想出解决办法,依然如下图:
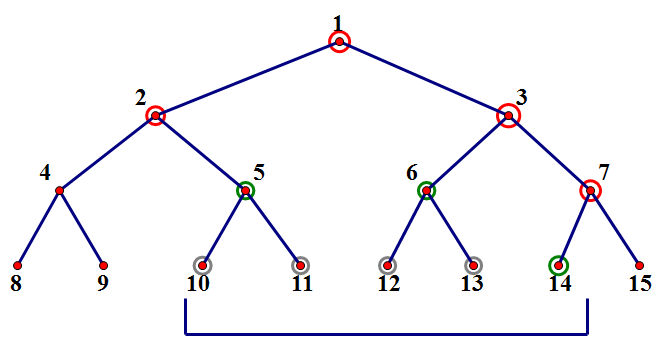
想要O(logn)地修改信息,就必须用与查询同样的方法:每碰到一个完全被包含的区间,就想办法在这个结点处记录下改动,然后返回,不碰下面的点。如何记录改动呢?这里引入标记(常称为“懒标记”,lazy tag),标记有两种含义,看个人习惯了,我程序中的标记表示:当标记存在时,说明该结点及祖先结点都已经完成过这个改动,而子结点均没有,也就是说,打上标记的同时应该维护该结点的信息。标记为何能发挥作用呢?因为如果我没必要将信息推到最底层,就应该把它留在上面,而什么时候应该把标记下推呢?就是需要它下去,也就是当某次操作没有完全覆盖这个结点时,需要下推标记,这样做与之前就下推的区别在哪呢?就是把之前不必要的操作转化为之后必要的操作,使得每次都只做必要的操作,而必要的操作显然是O(logn)的。具体实现见附程序。
2.查询?完全没有难度,只要跟单点修改一样找到结点(路上记得下推标记),然后到达叶子节点时里面存的就是要的答案了(因为所有改动都被推下来了)。
四、区间修改区间查询
1.修改:同“三”中的区间修改,维护标记即可。
2.查询:基本同“二”中的区间查询,只要路上记得下推标记即可。
五、几个注意事项
1.我的线段树写的是左闭右开区间,这样写的好处有——求出mid不用+-1,直接[l,mid)和[mid,r)即可;与stl的风格类似,左闭右开符合处理区间的习惯。
2.离散化用于线段树时,要注意区分线段树结点的实际含义:是代表一个左闭右开区间还是左闭右闭区间?是连续的区间拼成整棵线段树还是离散的?
例题
1.POJ 3468 A Simple Problem with Integers 区间修改区间查询(简单区间加减) 附程序
2.HihoCoder 1080 更为复杂的买卖房屋姿势 区间修改区间查询(区间置值与区间加减)
3.HihoCoder 1079 离散化 区间修改区间查询(离散化线段树) 题解传送门
P.S. HihoCoder第一次点进去要先登录,然后退掉再进一次即可。