【Java】二分查找、插值查找、斐波那契查找的实现，及分析

public class Search {
	
	/**1.顺序查找		时间复杂度为：O(n)
	*/
	public static int SequenceSearch(int[] a, int x) {
		for(int i=0;i<a.length;i++) {
			if(x==a[i])
				return i;
		}
		return -1;
	}
	
	
	/**2.二分查找,数组已有序  时间复杂度为: O(log(n))
		在有序数组中，设置下标left和right,每次从中间mid处找，若所需找的的x小于a[mid],则令right为mid-1,继续从该区域找；
		若所需找的的x大于a[mid],令left=mid+1,重复，直至left>right(注意，left和right相等也要考虑进去);
	*/
	public static int BinarySearchNoR(int[] a, int x){
		int left=0, right=a.length-1;
		
		while(left<=right){
			int mid = left+((right-left)>>1);
			if(a[mid]>x){
				right = mid-1;
			}
			else if(a[mid]<x){
				left = mid+1;
			}
			else{
				return mid;
			}
		}
		return -1;
	}
	
	//递归版
	public static int BinarySearchR(int[] a, int x, int left, int right){
		int mid = left+((right-left)>>1);
		
		if(left>right){
			return -1;
		}
		
		if(x<a[mid]){
			return BinarySearchR(a,x,left,mid-1);
		}
		else if(x>a[mid]){
			return BinarySearchR(a,x,mid+1,right);
		}
		else{
			return mid;
		}
		
		
	}
		
	
		
	/**3.插值查找
		插值查找算法类似于二分查找，不同的是插值查找每次从自适应mid处开始查找，例如我们要从1~100找5这个数，
		那我们就会从前边开始找，插值查找就是应用这种原理
		插值公式： mid = left+(x-a[left])/(a[right]-a[left])*(right-left);
	*/
	public static int InsertValueSearchR(int[] a, int x , int left, int right){
		
		if(x<a[0]||x>a[a.length-1]){	//不加这句会抛出异常，若找的数不在范围内，则mid可能越界
			return -1;
		}
		int mid = left + (x-a[left])/(a[right]-a[left])*(right-left);
		if(left>right){
			return -1;
		}
		if(x<a[mid]){
			return InsertValueSearchR(a,x,left,mid-1);
		}
		else if(x>a[mid]){
			return InsertValueSearchR(a,x,mid+1,right);
		}
		else{
			return mid;
		}
	}
	
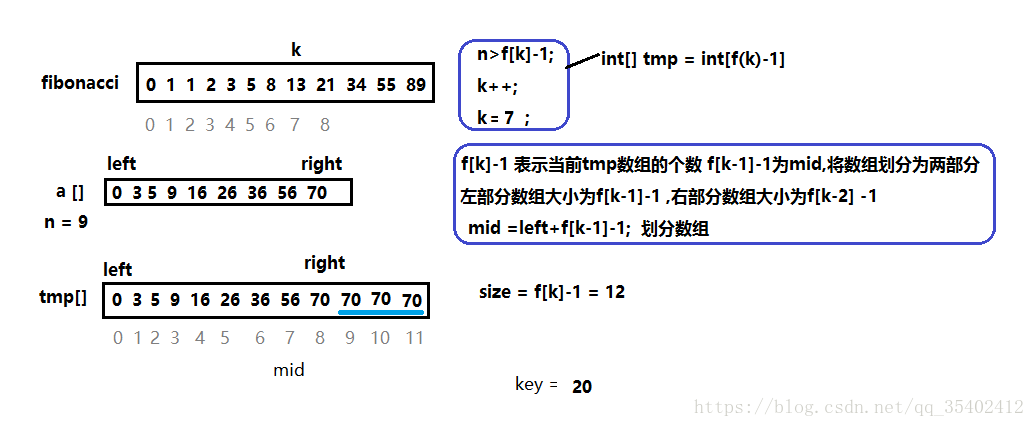
	/**Fibonacci查找（下面附图）
		基于二分查找的提升，也是有序查找，每次将数组分为两部分，不同的是使用斐波那契数的前两项和等于后一项的原理来实现；
		斐波那契数：0,1,1,2,3,5,8,13,21,34,55,89...
		创建一个临时数组，将目标数组拷贝该临时数组中，并使他的长度为斐波那契里的元素-1；且最后的元素都为right的值；
		if x<a[mid]
			right=mid-1;  区域划分到左
			k-=1;   左部分数组个数
		else if x>a[mid]
			left=mid+1;   区域划分到右
			k-=2;   右部分数组个数
		else   x==a[mid]
			if x<a.lenght
				return mid;
			else	在扩展的数组中找到，返回a的最后一个下标
				return right;
	*/
	//创建斐波那契数组
	public static void fibonacci(int[] f){
		f[0]=0;
		f[1]=1;
		for(int i=2;i<f.length;++i){
			f[i]=f[i-1]+f[i-2];
		}
		
	}
	
	public static int FibonacInsearch(int[] a, int x){
		int left=0, right=a.length-1;
		int k=0;
		int FIB_MAX = 20;
		int[] f = new int[FIB_MAX];
		fibonacci(f);
		
		while(a.length>f[k]-1){
			k++;
		}
		
		int[] tmp = new int[f[k]-1];
		System.arraycopy(a,0,tmp,0,a.length);//拷贝a元素到tmp中
		for(int i=a.length;i<f[k]-1;++i){	//right以后的值都相同
			tmp[i]=a[right];
		}
		
		while(left<=right){
			int mid = left+f[k-1]-1;
			if(x<a[mid]){
				right=mid-1;
				k-=1;
			}
			else if(x>a[mid]){
				left=mid+1;
				k-=2;
			}
			else{
				if(mid<a.length)
					return mid;
				else		//扩展里找到x，返回a的最后一个下标
					return a.length-1;

			}
		}
		return -1;
		
	}

       public static void main(String[] args) {
		int[] a = {5,1,3,8,9,6,4,7,8,5,2};
		System.out.println(SequenceSearch(a,9));
		System.out.println();
		int[] seq = {1,2,3,4,5,7,8,9};
		System.out.println("二分");
		System.out.println(BinarySearchNoR(seq,1));
		System.out.println(BinarySearchNoR(seq,6));
		System.out.println(BinarySearchNoR(seq,9));
		System.out.println("二分递归");
		System.out.println(BinarySearchR(seq,1,0,seq.length-1));
		System.out.println(BinarySearchR(seq,5,0,seq.length-1));
		System.out.println(BinarySearchR(seq,8,0,seq.length-1));
		System.out.println(BinarySearchR(seq,9,0,seq.length-1));
		System.out.println("插值查找");
		System.out.println(InsertValueSearchR(seq,0,0,seq.length-1));
		System.out.println(InsertValueSearchR(seq,1,0,seq.length-1));
		System.out.println(InsertValueSearchR(seq,8,0,seq.length-1));
		System.out.println(InsertValueSearchR(seq,6,0,seq.length-1));
		System.out.println("斐波那契查找");
		System.out.println(FibonacInsearch(seq,1));
		System.out.println(FibonacInsearch(seq,0));
		System.out.println(FibonacInsearch(seq,9));
		System.out.println(FibonacInsearch(seq,23));
	}

}

斐波那契：