lca即最近公共祖先,求最近公共祖先的方法大概有3种,其实是窝只听说过3种,这3种做法分别是倍增求lca,树剖求lca和tarjan求lca,但是窝只会前2种,所以这里只说前2种算法了。
首先是倍增求lca,倍增求lca的思想是不断的向上跳,直到跳到lca为止
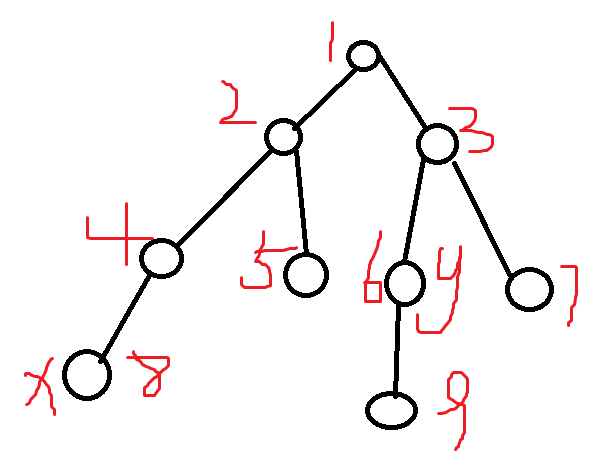
比如求这棵树中x和y的lca,首先让深度较深的点(x)跳到和深度较浅(y)的点同一个深度,然后先看一下x和y是不是同一个点了,如果是,那么不用再向上跳了,返回x即可。如果不是,需要继续往上跳,而这个往上跳的过程是判断如果跳到的那个深度x和y的祖先不是同一个就可以往上跳,因为如果是同一个的话很有可能跳过了,由于是这样跳的,所以最后x和y跳到的点是兄弟,这时只需要返回他们的父亲就好了。跳的过程相当于是对lca与x,y的深度差二进制分解,只不过不知道这个数是什么罢了。
模板:https://www.luogu.org/problemnew/show/P3379
代码:

1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 const int maxn=500005; 5 int n,m,s; 6 int x,y; 7 struct zhw{ 8 int to,last; 9 }tu[maxn<<1]; 10 int head[maxn],tot; 11 void add(int x,int y) 12 { 13 tot++,tu[tot].last=head[x],head[x]=tot,tu[tot].to=y; 14 } 15 int fa[maxn][18],deep[maxn]; 16 void dfs(int x) 17 { 18 for(int i=1;i<=17;++i)fa[x][i]=fa[fa[x][i-1]][i-1]; 19 for(int i=head[x];i;i=tu[i].last) 20 { 21 if(tu[i].to!=fa[x][0]) 22 { 23 fa[tu[i].to][0]=x,deep[tu[i].to]=deep[x]+1; 24 dfs(tu[i].to); 25 } 26 } 27 } 28 int lca(int x,int y) 29 { 30 if(deep[x]<deep[y])swap(x,y); 31 int t=deep[x]-deep[y]; 32 for(int i=17;i>=0;i--) 33 if((1<<i)&t)x=fa[x][i]; 34 if(x==y)return x; 35 for(int i=17;i>=0;i--) 36 { 37 if(fa[x][i]!=fa[y][i]) 38 x=fa[x][i],y=fa[y][i]; 39 } 40 return fa[x][0]; 41 } 42 int main() 43 { 44 scanf("%d%d%d",&n,&m,&s); 45 for(int i=1;i<n;++i) 46 { 47 scanf("%d%d",&x,&y); 48 add(x,y),add(y,x); 49 } 50 deep[s]=1;dfs(s); 51 while(m--) 52 { 53 scanf("%d%d",&x,&y); 54 printf("%d ",lca(x,y)); 55 } 56 return 0; 57 }
树剖那个以后有空了在写QAQ
