Codeforces Round #439 (Div. 2) Problem C (Codeforces 869C)

— This is not playing but duty as allies of justice, Nii-chan!

— Not allies but justice itself, Onii-chan!

With hands joined, go everywhere at a speed faster than our thoughts! This time, the Fire Sisters — Karen and Tsukihi — is heading for somewhere they've never reached — water-surrounded islands!

There are three clusters of islands, conveniently coloured red, blue and purple. The clusters consist of a, b and c distinct islands respectively.

Bridges have been built between some (possibly all or none) of the islands. A bridge bidirectionally connects two different islands and has length 1. For any two islands of the same colour, either they shouldn't be reached from each other through bridges, or the shortest distance between them is at least 3, apparently in order to prevent oddities from spreading quickly inside a cluster.

The Fire Sisters are ready for the unknown, but they'd also like to test your courage. And you're here to figure out the number of different ways to build all bridges under the constraints, and give the answer modulo 998 244 353. Two ways are considered different if a pair of islands exist, such that there's a bridge between them in one of them, but not in the other.

Input

The first and only line of input contains three space-separated integers a, b and c (1 ≤ a, b, c ≤ 5 000) — the number of islands in the red, blue and purple clusters, respectively.

Output

Output one line containing an integer — the number of different ways to build bridges, modulo 998 244 353.

Examples

input

1 1 1

output

8

input

1 2 2

output

63

input

1 3 5

output

3264

input

6 2 9

output

813023575

Note

In the first example, there are 3 bridges that can possibly be built, and no setup of bridges violates the restrictions. Thus the answer is 23 = 8.

In the second example, the upper two structures in the figure below are instances of valid ones, while the lower two are invalid due to the blue and purple clusters, respectively.

---

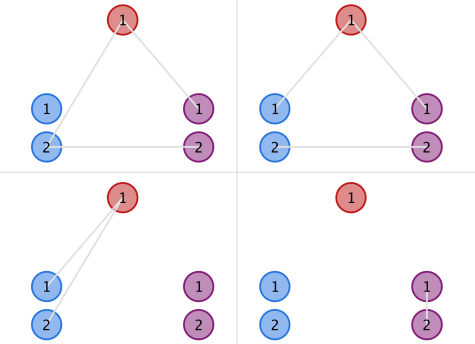
　　题目大意 有3个群岛，每个群岛中有一些互不相同的岛屿，现在建一些桥，使得同一群岛内的两个岛屿要么不连通要么最短路至少经过3条桥。给定三个群岛包含的岛数，求合法的建桥的方案数。

　　显然有某个群岛中的某个岛只能连接其他群岛中的一个岛。群岛与群岛之间的建桥互相独立，所以考虑分开计算。

　　考虑两个群岛之间建立k座桥，那么方案数就是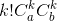

　　所以对于两个群岛之间的建桥方案数for一遍就求完了，最后把答案乘起来就行了。

Code

/**
 * Codeforces
 * Problem#869C
 * Accepted
 * Time: 30ms
 * Memory: 0k
 */ 
#include <bits/stdc++.h>
#ifndef WIN32
#define Auto "%lld"
#else
#define Auto "%I64d"
#endif
using namespace std;

#define ll long long

void exgcd(ll a, ll b, ll& d, ll &x, ll &y) {
    if(!b)    {
        d = a, x = 1, y = 0;
    } else {
        exgcd(b, a % b, d, y, x);
        y -= (a / b) * x; 
    }
}

ll inv(ll a, ll n) {
    ll d, x, y;
    exgcd(a, n, d, x, y);
    return (x < 0) ? (x + n) : (x);
}

const int moder = 998244353;
int a, b, c;

inline void init() {
    scanf("%d%d%d", &a, &b, &c); 
}

long long calc(int x, int y) {
    long long rt = 1;
    long long Px = 1, Py = 1;
    for(int i = 1; i <= x && i <= y; i++) {
        Px = (Px * (x - i + 1) % moder) * inv(i, moder) % moder;
        Py = (Py * (y - i + 1)) % moder;
        rt = (rt + (Px * Py % moder)) % moder;
    }
    return rt;
}

inline void solve() {
    long long ra = calc(a, b);
    long long rb = calc(b, c);
    long long rc = calc(c, a);
    long long res = ((ra * rb) % moder) * rc % moder;
    printf(Auto, res);
}

int main() {
    init();
    solve();
    return 0;
}