笔记: Manacher

KSkun大佬的blog

Oh how confused this konjac is! It is tring to write down some notes to help itself!

洛谷-【模板】manacher

给出一个字符串 S ,求 S 中最长回文串的长度 。

• 朴素算法是以每一个点和间隔为中点往外扫。时间复杂度 (O(n^2))

• 马拉车算法 时间复杂度 (O(n))

首先，构造一个字符串 (s2) ,将字符串 (s1) 的尾以及间隔处插入 #,头部插入$

如果s1=aaa,则s2=$a#a#a#​

这样做的效果是把所有回文串对应到了一个奇回文串上，将对接下来的操作有帮助。

设一个数组 (p_i) 表示第 (i) 个字符的回文半径。

例如 $#a#b#c#b#a#a#b#c#b#a# 其中第一个c的回文串就是#a#b#c#b#a#

回文半径就是6。

如何用 (p_{1...i-1}) 推出 (p_i) ？

设 (mx) 为当前最大回文串右边界， (id) 为当前最大回文串对称中心。

则 (mx=id+p[id])

我们先求出以 (i)为中心的回文半径至少有多长。

• i<mx 时：

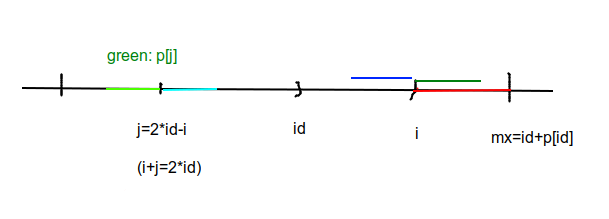
(p_i) 的值可以通过 (p_j) 转移而来，因为左右是关于id对称的。也就是说，深蓝=浅蓝，深绿=浅绿。需要注意的是，(mx-i) 可能会 (<p_j) 此时 (p_i=mx-i)

所以 (p_i=min(p_{2*id-i},mx-i))

• i>mx 时，直接先设 (p_i=1)。

之后再往两遍扩展即可。求出 (p_i) 后要更新 (mx) 和 (id) 。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=11e6+10;
int n,p[N<<1];
char s1[N],s2[N<<1];
int manacher(){
    int tot=0;
    s2[tot++]='$',s2[tot++]='#';
    for(int i=1;i<=n;i++)
        s2[tot++]=s1[i],s2[tot++]='#';
    tot--;
    int mxlen=0,mx=0,id=0;
    for(int i=1;i<=tot;i++){
        if(i<mx) p[i]=min(p[id*2-i],mx-i);
        else p[i]=1;
        while(s2[i-p[i]]==s2[i+p[i]]) p[i]++;

        if(mx<i+p[i]) mx=i+p[i],id=i;
        mxlen=max(mxlen,p[i]-1);
    }
    return mxlen;
}
int main(){
    scanf("%s",s1+1);
    n=strlen(s1+1);
    printf("%d
",manacher());
    return 0;
}