极大似然估计(Maximum likelihood estimation, 简称MLE)是很常用的参数估计方法,极大似然原理的直观想法是,一个随机试验如有若干个可能的结果A,B,C,...,若在一次试验中,结果A出现了,那么可以认为实验条件对A的出现有利,也即出现的概率P(A)较大。也就是说,如果已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值
EM算法:Expectation-Maximization:
最大似然:
已知:(1)样本服从分布的模型, (2)观测到的样本
求解:模型的参数
总的来说:极大似然估计就是用来估计模型参数的统计学方法
最大似然数学问题(100名学生的身高问题)
样本集X={x1,x2,…,xN} N=100
概率密度:p(xi|θ)抽到男生i(的身高)的概率
独立同分布:同时抽到这100个男生的概率就是他们各自概率的乘积
θ是服从分布的参数
最大似然函数:l(a) = sum(logp(xi;a)) (对数是为了乘法转加法)
什么样的参数 能够使得出现当前这批样本的概率最大
已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,
参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值。
本文以一个简单的离散型分布的例子,模拟投掷硬币估计头像(head)向上的概率。投掷硬币落到地面后,不是head向上就是tail朝上,这是一个典型的伯努利实验,形成一个伯努利分布,有着如下的离散概率分布函数: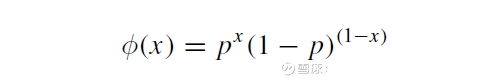
其中,x等于1或者0,即结果,这里用1表示head、0表示tail。
对于n次独立的投掷,很容易写出其似然函数:
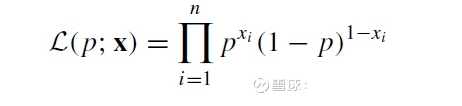
现在想用极大似然估计的方法把p估计出来。就是使得上面这个似然函数取极大值的情况下的p的取值,就是要估计的参数。
首先用Python把投掷硬币模拟出来:
from scipy.stats import bernoulli # 生成样本 p_1 = 1.0 / 2 # 假设样本服从p为1/2的bernouli分布 fp = bernoulli(p_1) # 产生伯努利随机变量 xs = fp.rvs(100) # 产生100个样本 print(xs[:30]) # 看看前面30个 # [0 1 1 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 1 1 0 1 1 0 0 1 0 0 0 1]
通过此模拟,使用sympy库把似然函数写出来:
import sympy
import numpy as np
# 估计似然函数
x, p, z = sympy.symbols('x p z', positive=True)
phi = p**x*(1-p)**(1-x) #分布函数
L = np.prod([phi.subs(x, i) for i in xs]) # 似然函数
print(L)
# p**52*(-p + 1)**48
从上面的结论可以看出,作100次伯努利实验,出现positive、1及head的数目是52个,相应的0也就是tail的数目是48个,比较接近我们设的初始值0.5即1.0/2(注意:现在我们假设p是未知的,要去估计它,看它经过Python的极大似然估计是不是0.5!)。
下面,我们使用Python求解这个似然函数取极大值时的p值:
logL = sympy.expand_log(sympy.log(L)) sol = sympy.solve(sympy.diff(logL, p), p) print(sol) [13/25]
结果没有什么悬念,13/25的值很接近0.5!
取对数后,上面Python的算法最后实际上是求解下式为0的p值:
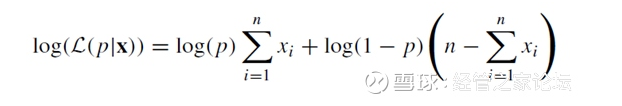
上式留给网友自行推导,很多资料都可找到该式。这个式子,是著名的Logistic回归参数估计的极大似然估计算法的基础。
进一步,为了更加直观的理解投掷硬币的伯努利实验,我们给出以均值(均值为100*0.5=50)为中心对称的加总离散概率(概率质量函数(probability mass function),Python里面使用pmf函数计算):
from scipy.stats import binom b = binom(100, .5) # 以均值为中心对称的加总概率 g = lambda x: b.pmf(np.arange(-x, x) + 50).sum() print(g(10)) 0.9539559330706295
对于上面的Python代码,可以通过下图更好地去理解:
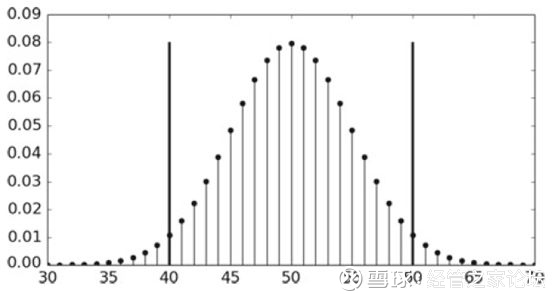
把这20个离散的概率全部显示出来,也可以看到在0.08左右取到它们的最大值
本文针对简单的离散概率质量函数的分布使用Python进行了极大似然估计,同时该方法可以应用于连续分布的情形,只要通过其概率密度函数得出其似然函数即可。