0-1 背包

今天就来说一下背包问题吧，就讨论最常说的 0-1 背包问题。描述：

给你一个可装载重量为 W 的背包和 N 个物品，每个物品有重量和价值两个属性。其中第 i 个物品的重量为 wt[i]，价值为 val[i]，现在让你用这个背包装物品，最多能装的价值是多少？

 

 

 

第一步要明确两点，「状态」和「选择」。

先说状态，如何才能描述一个问题局面？只要给几个物品和一个背包的容量限制，就形成了一个背包问题呀。所以状态有两个，就是「背包的容量」和「可选择的物品」。

再说选择，也很容易想到啊，对于每件物品，你能选择什么？选择就是「装进背包」或者「不装进背包」嘛。

明白了状态和选择，动态规划问题基本上就解决了，只要往这个框架套就完事儿了：

for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 择优(选择1，选择2...)

 

dp[i][w] 的定义如下：对于前 i 个物品，当前背包的容量为 w，这种情况下可以装的最大价值是 dp[i][w]。

比如说，如果 dp[3][5] = 6，其含义为：对于给定的一系列物品中，若只对前 3 个物品进行选择，当背包容量为 5 时，最多可以装下的价值为 6。

 

int[][] dp[N+1][W+1]
dp[0][..] = 0
dp[..][0] = 0

for i in [1..N]:
    for w in [1..W]:
        dp[i][w] = max(
            把物品 i 装进背包,
            不把物品 i 装进背包
        )
return dp[N][W]

二维 dp

int main() {
    //可装载重量为 W 的背包和 N 个物品
    int N = 3, W = 4;
    std::vector<int> wt = {2, 1, 3};
    std::vector<int> val = {4, 2, 3};
    std::vector<std::vector<int>>dp(N+1,std::vector<int>(W+1,0));
    for(int n = 1;n <= N;++n) {
        for(int w = 1;w <= W;++w) {
            if(w-wt[n-1]< 0) {
                dp[n][w] = dp[n-1][w];
            } else {
                //由于i是从1开始的，所以 val 和 wt 的索引是 i-1 时表示第 i 个物品的价值和重量。
                dp[n][w] = std::max(dp[n-1][w],val[n-1] + dp[n-1][w-wt[n-1]]); 
            }
        }
    }
    std::cout << dp[N][W] << std::endl;
    return 0;
}

二维 dp 投影到一维 dp

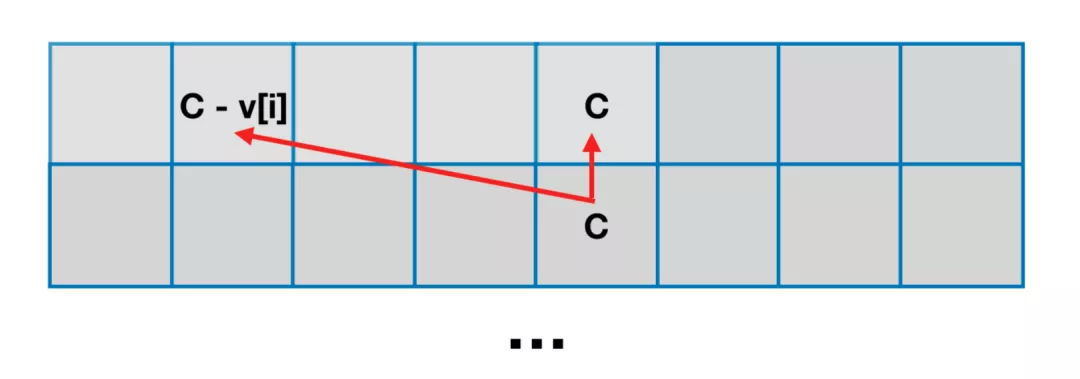
 一维dp

注意一维 dp 遍历顺序。倒序防止覆盖

#include<vector>
#include<iostream>
#include<string>
int main() {
    //可装载重量为 W 的背包和 N 个物品
    int N = 3, W = 4;
    std::vector<int> wt = {2, 1, 3};
    std::vector<int> val = {4, 2, 3};
    std::vector<int>dp(W+1,0);
    for(int n = 1;n <= N;++n) {
        for(int w = W;w >=0;--w) {
            if(w-wt[n-1]< 0) {
                dp[w] = dp[w];
            } else {
                //由于i是从1开始的，所以 val 和 wt 的索引是 i-1 时表示第 i 个物品的价值和重量。
                dp[w] = std::max(dp[w],val[n-1] + dp[w-wt[n-1]]); 
            }
        }
    }
    std::cout << dp[W] << std::endl;
    return 0;
}

https://mp.weixin.qq.com/s/xmgK7SrTnFIM3Owpk-emmg