求把(N*M(1le N,M le 11)) 的棋盘分割成若干个(1 imes 2) 的长方形,有多少种方案。例如当 (N=2,M=4)时,共有5种方案。当(N=2,M=3)时,有3种方案。
NM只有11,八九不离十可以状压了,反正得挨个铺,所以从上到下考虑。假如现在铺好了前(i) 层,基本思想就是从(i) 层的状态转移到(i+1)层的状态。但是该如何表示?观察一下铺满第 (i) 层的样子(必须保证第(i)层是满的,也就是说有的可以凸出来到(i+1)层但是要保证(i)层是满的)
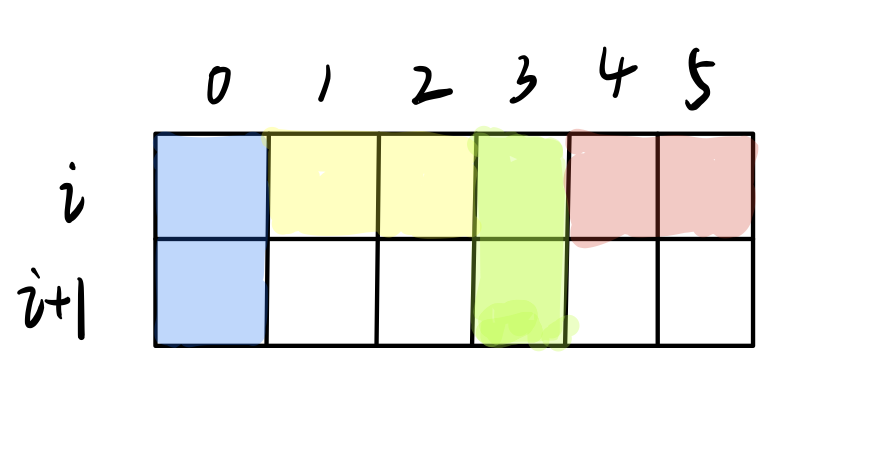
对于第 i 行中竖着放的,第 (i+1) 层要受到牵连,它必须补全竖着放置的上一半才行。但对于横着放的,第(i+1)层则无所谓。
所以我们可以用二进制中的 1 来表示他是否是竖着放置的上一半。为0则为其他状况。
(d[i][j])表示第 (i) 的形态为(j) 时,前(i) 行分割方案的总数。 (j) 是用十进制整数记录的 (m) 位二进制数。考虑(i+1)行的状态(k)在满足什么情况下转移是合法的。
- (j)中为 1 的位,(k)中必须为0
- (j)中为 0 的位,(k)中可以为1,但 k 要是为 0,就必须是连续的偶数个0(想一想为什么)
对于第一条,可以用 (i&j = 0) 来判断,对于第二条,有(z = i|j),那么 z 的二进制表示中,每一段连续的 0 都必须有偶数个。(这些0代表若干个横着的 (1 imes 2) 长方形,奇数个0无法分割成这种形态。
#include <iostream>
#include <cstdio>
using namespace std;
int n,m;
long long f[12][1<<11];
bool in_s[1<<11];
int main(){
while(cin>>n>>m && n){
//先把合法状态筛出来,即二进制表示中每一段连续的0都有偶数个
for(int i=0;i<1<<m;i++){
bool cnt = 0,has_odd = 0;
for(int j=0;j<m;j++)
if(i >> j & 1)has_odd |= cnt,cnt=0;
else cnt ^= 1;
in_s[i] = (has_odd | cnt) ? 0 : 1;
}
f[0][0] = 1;
for(int i=1;i<=n;i++){
for(int j=0;j<1<<m;j++){
f[i][j] = 0;
for(int k=0;k< 1<<m;k++){
if((j & k) == 0 && in_s[j|k])
f[i][j] += f[i-1][k];
}
}
}
cout<<f[n][0]<<endl;
}
return 0;
}