[Luogu2458][SDOI2006]保安站岗

题目描述

五一来临，某地下超市为了便于疏通和指挥密集的人员和车辆，以免造成超市内的混乱和拥挤，准备临时从外单位调用部分保安来维持交通秩序。

已知整个地下超市的所有通道呈一棵树的形状；某些通道之间可以互相望见。总经理要求所有通道的每个端点（树的顶点）都要有人全天候看守，在不同的通道端点安排保安所需的费用不同。

一个保安一旦站在某个通道的其中一个端点，那么他除了能看守住他所站的那个端点，也能看到这个通道的另一个端点，所以一个保安可能同时能看守住多个端点（树的结点），因此没有必要在每个通道的端点都安排保安。

编程任务：

请你帮助超市经理策划安排，在能看守全部通道端点的前提下，使得花费的经费最少。

输入输出格式

输入格式：

第1行 n，表示树中结点的数目。

第2行至第n+1行，每行描述每个通道端点的信息，依次为：该结点标号i（0<i<=n），在该结点安置保安所需的经费k（<=10000），该边的儿子数m，接下来m个数，分别是这个节点的m个儿子的标号r1，r2，...，rm。

对于一个n（0 < n <= 1500）个结点的树，结点标号在1到n之间，且标号不重复。

输出格式：

最少的经费。

如右图的输入数据示例

输出数据示例：

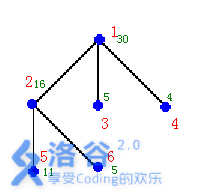
输入输出样例

输入样例#1： 

6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0

输出样例#1： 

25

说明

样例说明：在结点2，3，4安置3个保安能看守所有的6个结点，需要的经费最小：25

---

设f[i][0]表示选自己，f[i][1]选儿子不选自己,f[i][2]选父亲不选自己的最小代价。

于是f[i][0] = sum(min(f[v][1],f[v][2],f[v][0])),

f[i][2] = sum(min(f[v][0],f[v][1]))，因为承诺了这个点不选，那么它的儿子不能选父亲，

对于f[i][1],我们必须保证儿子中至少有一个选了自己，所以我们可以记录一下有没有儿子选自己。

如果有，则直接计算f[i][1] = sum(min(f[v][0],f[v][1])。

如果没有，那么从儿子中选择一个f[v][0]-f[v][1]最小的加上就行了。

还要注意的是，如果这个节点是叶子节点，那么它不存在选自己的儿子，所以f[i][1]直接设成inf就行了。

---

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm> 
using namespace std;
inline int read(){
    int res=0;char ch=getchar();
    while(!isdigit(ch))ch=getchar();
    while(isdigit(ch)){res=(res<<3)+(res<<1)+(ch^48);ch=getchar();}
    return res;
}
int n;
struct edge{
    int nxt, to;
}ed[3005];
int head[1505], cnt;
inline int add(int x, int y) 
{
    ed[++cnt] = (edge){head[x], y};
    head[x] = cnt;
}
int val[1505];
bool lev[1505];
int f[1505][3];//0:选自己，1:选儿子，2:选父亲 

void dfs(int x, int fa)
{
    f[x][0] = val[x];
    if (lev[x]) f[x][1] = 1e9;
    int minn = 1e9;
    bool flag = 0;
    for (int i = head[x] ; i ; i = ed[i].nxt)
    {
        int to = ed[i].to;
        if (to == fa) continue;
        dfs(to, x);
        f[x][0] += min(f[to][0], min(f[to][1], f[to][2]));
        f[x][2] += min(f[to][0], f[to][1]);
        if (f[to][0] < f[to][1]) flag = 1;
        else minn = min(minn, f[to][0] - f[to][1]);
        f[x][1] += min(f[to][1], f[to][0]);
    }
    if (!flag) f[x][1] += minn;
}

int main()
{
    n = read();
    for (int i = 1 ; i <= n ; i ++)
    {
        int x = read();
        val[x] = read();
        int num = read();
        if (!num) lev[x] = 1;
        while(num--)
        {
            int y = read();
            add(x, y), add(y, x);
        }
    }
    dfs(1, 0);
    printf("%d
", min(f[1][0], f[1][1]));
    return 0;
}

 $sum_{age=16}^{18} hardworking = success$