大话数据结构 -06 树

一、普通树

树中的节点是一对多的关系。具有以下特点： 

1. n>0时，根节点是唯一的，不可能存在多个根节点。

2. 每个节点有零个至多个子节点；除了根节点外，每个节点有且仅有一个父节点。根节点没有父节点。

相关概念：

1. 子树：除了根节点外，每个子节点都可以分为多个不相交的子树。
2. 孩子与双亲：若一个结点有子树，那么该结点称为子树根的"双亲"，子树的根是该结点的"孩子"。
3. 兄弟：具有相同双亲的节点互为兄弟。
4. 节点的度：一个节点拥有子树的数目。等价与该节点拥有孩子的数目。（子树个数=孩子节点）树的度=各个节点度的最大值
5. 叶子：没有子树，也即是度为0的节点。
6. 分支节点：除了叶子节点之外的节点，也即是度不为0的节点。
7. 内部节点：除了根节点之外的分支节点。（非根节点、非叶节点）
8. 层次：根节点为第一层，其余节点的层次等于其双亲节点的层次加1.
9. 树的高度：也称为树的深度，树中节点的最大层次。
10. 有序树：树中节点各子树之间的次序是重要的，不可以随意交换位置。
11. 无序树：树中节点各子树之间的次序是不重要的。可以随意交换位置。
12. 森林：0或多棵互不相交的树的集合。

参考：https://www.cnblogs.com/QG-whz/p/5168620.html

性质：

「1」树的结点无左、右之分，最大度数没有限制。

「2」树的结点个数至少为1，而二叉树的结点个数可以为0。

二、二叉树

二叉树或者为空集，或者由一个根节点和两棵互不相交的、分别称为左子树和右子树的二叉树组成。从定义可以看出一棵二叉树：

1. 二叉树是有序树，区分左子树与右子树，不可以随意交换子树位置。

2. 一个节点的子树数量取值范围为0，1，2。0代表该节点是叶子节点，1代表该节点只有左子树或只有右子树，2代表该节点有左右子树。

参考：https://www.cnblogs.com/QG-whz/p/5168620.html

性质：

「1」二叉树的子树有左右之分，次序不能颠倒。

「2」深度为k的二叉树至多有2^k-1个结点；（等比数列1+2+4+…+2^(k-1) = 2^k-1）。

「3」对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0 = n2 + 1。

证明：二叉树节点度数最大为2，则 ： n = n0 + n1 + n2 (等式一)
从孩子个数角度出发： 度为0的节点没有孩子， 度为1的节点没有1个孩子，度为2的节点有2个孩子，孩子总数为 n00 + n11 +n2 2 = n1+2n2；树的所有节点中，只有根不是任何节点的孩 子，因此有 n -1 = n1 + 2* n2 ,即 n = n1 + 2* n2 + 1. （等式二）
由等式一等式而可以推出 n0 = n2 +1

 「4」具有n个节点的完全二叉树的高度为至少为log2(n+1)

证明：高度为h的二叉树最多有2{h}–1个结点。反之，对于包含n个节点的二叉树的高度至少为log2(n+1)。

 「5」如果对一棵有n个节点的完全二叉树的节点按层序编号（从第一层开始到最下一层，每一层从左到右编号），对任一节点i有：

1. 如果i=1 ，则节点为根节点，没有双亲。如果i>1，则其双亲是结点「i/2」
2. 如果2 * i > n ，则节点i没有左孩子 ；否则其左孩子节点为2*i . （n为节点总数）
3. 如果2 * i+1>n ，则节点i没有右孩子；否则其右孩子节点为2*1+1

满二叉树：

一颗深度为k且有2^k-1个结点的二叉树称为满二叉树。 即：除叶子结点外的所有结点均有两个子结点。节点数达到最大值。所有叶子结点必须在同一层上。

节点数和深度的关系 n=2^k-1

性质：

「1」如果一颗树深度为h，最大层数为k，且深度与最大层数相同，即k=h;

「2」第k层的结点数是： 2^(k-1)

「3」总节点数一定是奇数。

「4」树高：h=log₂(n+1)。

参考：https://www.cnblogs.com/myjavascript/articles/4092746.html

 完全二叉树：

 若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边（在最后一层上只缺少右边的若干结点），这就是完全二叉树。

节点数的范围是2^(k-1)-1<N<=2^k-1

与满二叉树的区别是，他的最后一行可能不是完整的，但绝对是右方的连续部分缺失。

参考：https://www.cnblogs.com/mapc/articles/4842256.html

 性质：

「1」 树高h=「log₂n」 + 1。（「x」表示不大于x的整数）

「2」同样节点数的二叉树，完全二叉树的深度最小。（*满二叉树与完全二叉树深度一样 *其他的二叉树大于等于完全二叉树）

三、树的存储结构（三种）

1）双亲表示法

2）孩子表示法

3）孩子兄弟表示法:把一颗复杂的树处理成二叉树

具体：https://www.jianshu.com/p/6ba5743f41f7

四、二叉树的存储结构

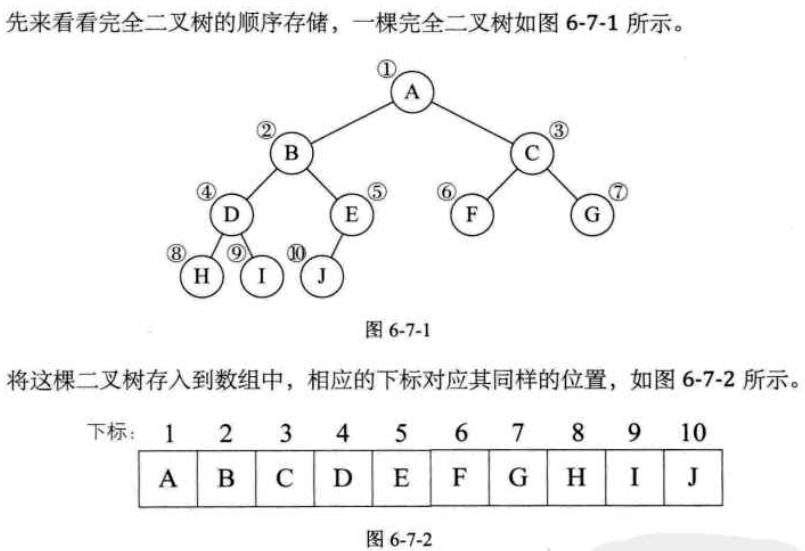
1）顺序存储结构（一般只用于完全二叉树，非完全浪费空间）

 2）二叉链表

 二叉树每个结点最多有两个孩子，因此设计一个数据域和两个指针域

五、遍历二叉树

1）前序遍历（树为空直接返回）（跟结点在前）

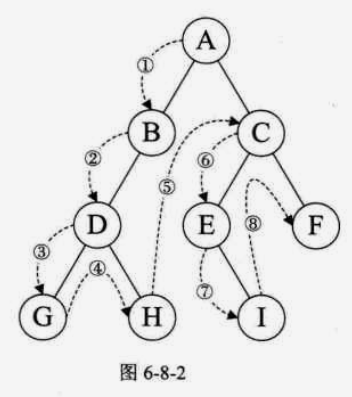
前序遍历算法

2）中序遍历（根结点在中间）

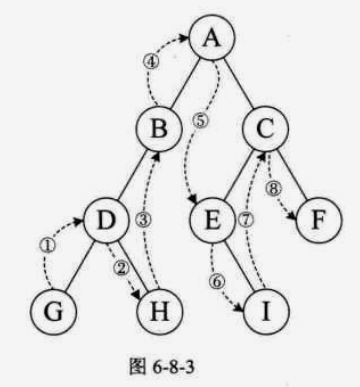
中序遍历算法

3）后序遍历（根结点最后）

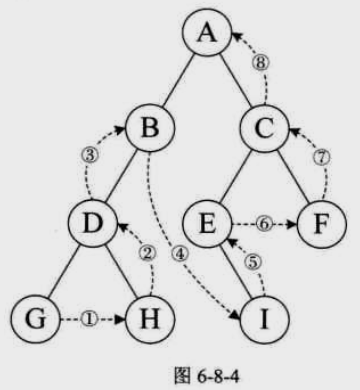
后序遍历算法

4）层序遍历

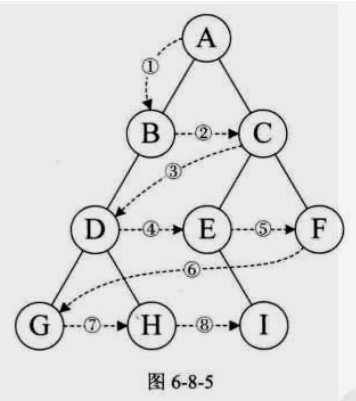
 5）推导遍历结果

六、二叉树的建立

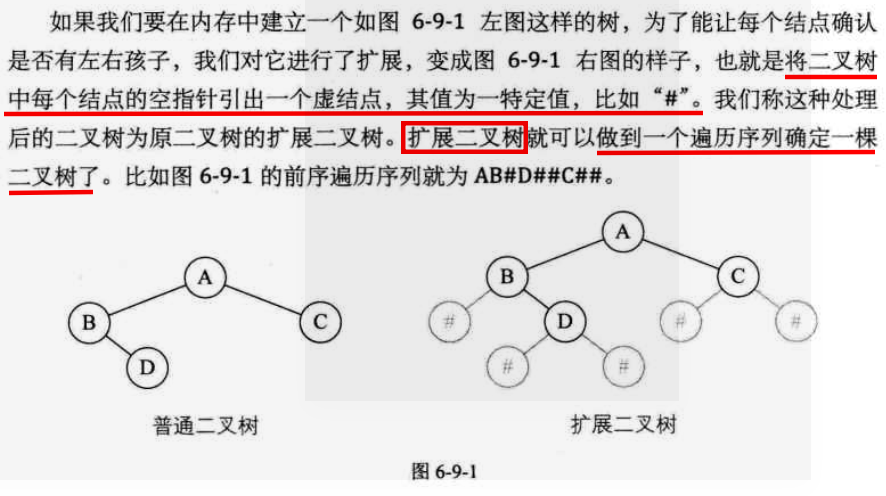
七、线索二叉树

对于一个有n个结点的二叉链表，每个结点有左右两个指针域，一共有2n个指针域。而n个结点的二叉树有n-1条分支线，即：共有2n-(n-1)=n+1个空指针域。

 因此，提出了一种方法，利用原来的空链域存放指向前驱或后继的指针，这种指向前驱或后继的指针称为线索。加上线索的二叉链表称为线索链表，相应的二叉树称为线索二叉树。

线索二叉树相当于把 一颗二叉树变成了双向链表。即：在遍历过程中修改空指针的过程。

线索二叉树的结构实现：

中序遍历线索化递归代码：（？？？）

上述代码除了加粗字体外，与中序遍历递归代码几乎一致，将原本是打印结点的功能改成了线索化的功能。

（P216/192...）