【Course】Machine learning：Week 1-Lecture1&Lecture2

一、Introduction

• 略

二、Linear Regression with One Variable

• 0 Model

本节课的问题是房价预测问题：

- ### 1 model and cost function Andrew Ng在cost function Intuition I中对hypothesis和cost function做了对比 $ heta_0$已经假设等于0，于是只剩下一个参数$ heta_1$。

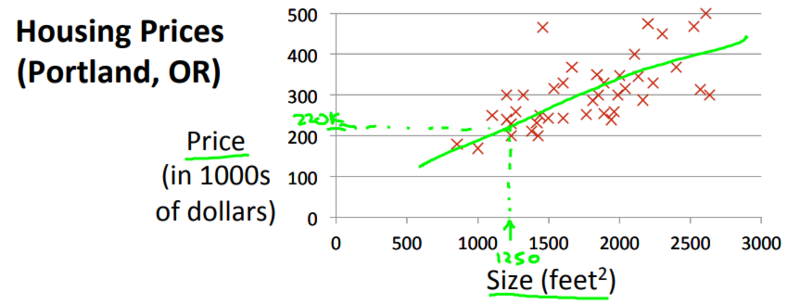
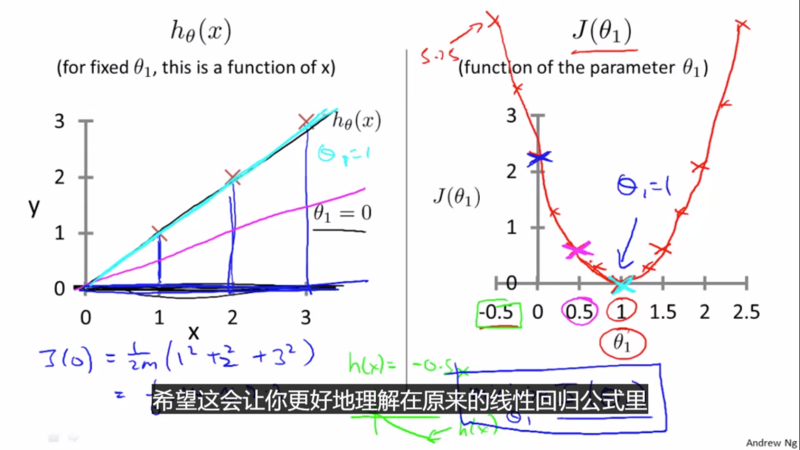
• hypothesis (h_{ heta}(x))：是x的函数（对于一个固定的( heta_1)）

• cost function (J( heta_1))：是参数( heta_1)的函数

• 2 Gradient Descent

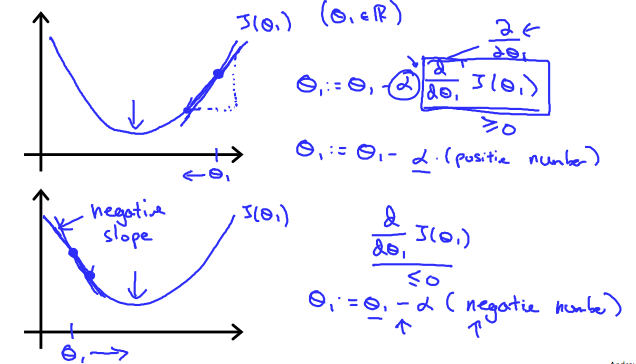
• （1）针对这个单变量线性回归问题，如下图，有个要点：

- $ heta_1$和$ heta_2$要同时更新，不然就会出错

• （2）梯度下降算法公式：

[ heta_j := heta_j - alpha frac{partial}{partial heta_j} J( heta_0, heta_1) ]

无论(frac{partial}{partial heta_j} J( heta_0, heta_1))的符号是什么，( heta_1)都会收敛到使得cost function取得最小值的点，符号是正时，( heta_1)减小，符号是负时，( heta_1)增大。

• （3）$alpha的值要合理

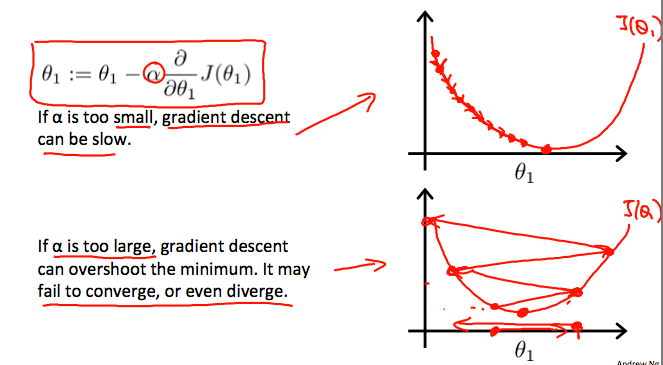
• 此外

- #### （4）$ heta_j := heta_j - alpha frac{partial}{partial heta_j} J( heta_0, heta_1)$的推导过程

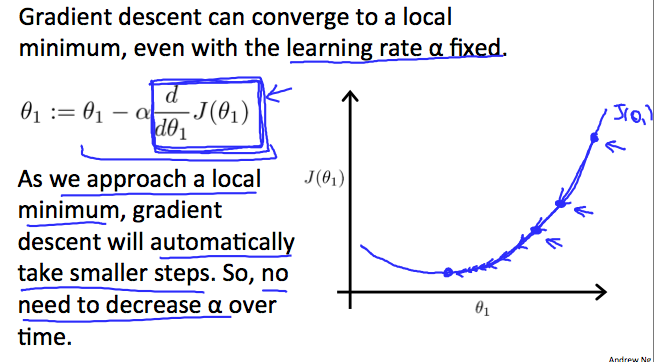
[egin{aligned} frac{partial}{partial heta_{j}} J( heta) &=frac{partial}{partial heta_{j}} frac{1}{2}left(h_{ heta}(x)-y ight)^{2} \ &=2 cdot frac{1}{2}left(h_{ heta}(x)-y ight) cdot frac{partial}{partial heta_{j}}left(h_{ heta}(x)-y ight) \ &=left(h_{ heta}(x)-y ight) cdot frac{partial}{partial heta_{j}}left(sum_{i=0}^{n} heta_{i} x_{i}-y ight) \ &=left(h_{ heta}(x)-y ight) x_{j} end{aligned} ]

• （5）一个梯度下降的例子

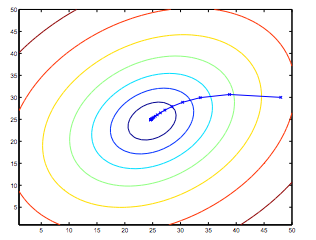
梯度下降的轨迹，初始值为(48,30)