zoukankan html css js c++ java

LeetCode 树（N叉树遍历和二叉树遍历及其他）

递归是一种程序设计的方式和思想。计算机在执行递归程序时，是通过栈的调用来实现的。
栈，从抽象层面上看，是一种线性的数据结构，这中结构的特点是“先进后出”，即假设有a，
b，c三个元素，依次放某个栈式存储空间中，要从该空间中拿到这些元素，那么只能以c、b、a的顺序得到。
递归程序是将复杂问题分解为一系列简单的问题，从要解的问题起，逐步分解，并将每步分解得到的问题放入“栈”中，这样栈顶是最后分解得到的最简单的问题，
解决了这个问题后，次简单的问题可以得到答案，以此类推。
分解问题是进栈（或者说压栈）的过程，解决问题是一个出栈的过程。

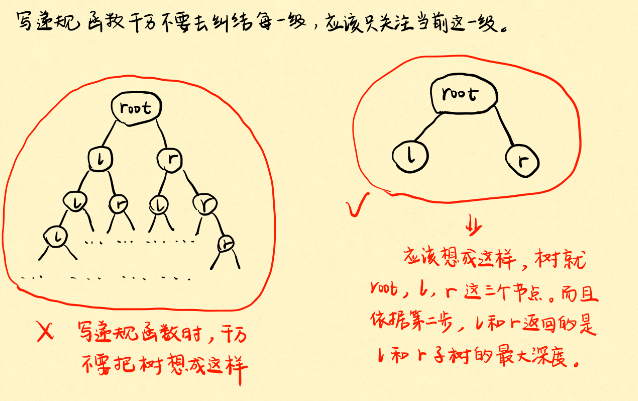
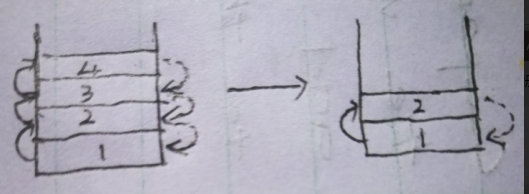
从栈的调用角度看，如果你的视角是左边那样把调用想象如此之复杂时，不如像右边一样，只是简简单单的调用一次。这样更好理解！

评论区C++递归代码

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    vector<int> preorder(Node* root) {
        vector<int> res={};
        PreOrder(root,res);
        return res;
        
    }
    void PreOrder(Node* T,vector<int> &res){
        if(T==NULL)
            return;
        res.push_back(T->val);
        for(int i=0;i!=(T->children).size();i++){
            PreOrder((T->children)[i],res);
        }
    }
};

迭代代码：

利用栈来实现。

需要注意的点在程序中标注：

必须看完评论区的代码后，自己不照着评论区中的代码写一遍。才会知道有哪些需要注意的点。

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    vector<int> preorder(Node* root) {
        vector<int> result;
        if(root==NULL){
            return  result;
        }
        stack<Node*> stk;
        stk.push(root);
        while(!stk.empty()){//注意判断条件是!stk.empty()而不是stk!=NULL
            Node* t=stk.top();
            stk.pop();
            result.push_back(t->val);
            for(int i=t->children.size()-1;i>=0;--i){//注意for循环中的第一条是t->children.size()而不是root->children.size()。 注意最后一条是--i,而不是i--
                stk.push(t->children[i]);
            }
        }
        return result;
    }
};

参考的上一题的递归代码。

发现一个很重要的需要注意的地方：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    vector<int> postorder(Node* root) {
        vector<int> vec={};
        PostOrder(root,vec);
        return vec;
    }
    void PostOrder(Node* root,vector<int> &vec){//这里的&必须要加上，不然会出现这样的结果
        if(root==NULL){
            return;
        }
        for(int i=0;i!=root->children.size();i++){
            PostOrder((root->children)[i],vec);
        }
        vec.push_back(root->val);
    }
};

如果不加入引用(&)的话，是不会改变vector类似的这样的数据结构的。

迭代：

出错，原因：这里的代码只适用于两层的树，不具有普适性。如果有第三层树就不适用了。所以还要再改善！。

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    vector<int> postorder(Node* root) {
        Node* m=root;
        vector<int> vec;
        if(root==NULL){
            return vec;
        }
        stack<Node*> stk;
        stk.push(root);
        Node* f=stk.top();
        for(int i=f->children.size()-1;i>=0;--i){//把所有元素都入栈
            stk.push(f->children[i]);
            if(f->children[i]->children.size()){//子树若是有子树，则先把子树压栈，后压栈子树的子树   这个只适用于两层的树！！
                for(int t=f->children[i]->children.size()-1;t>=0;--t){
                    stk.push(f->children[i]->children[t]);
                    }
                } 
            }
         while(!stk.empty()){//所有元素进vec
            Node* k=stk.top();
            vec.push_back(k->val);
            stk.pop();
            
         }
        return vec;
    }  
};

对照评论区的代码，修改后：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    void postorder(Node* &root,stack<Node*> &st,vector<int> &ans){
        st.push(root);
        stack<int> st2;
        while(!st.empty()){
            Node* node=st.top();
            st2.push(node->val);
            st.pop();
            for(int i=0;i<(node->children.size());i++){
                st.push(node->children[i]);
            }    
        }
        while(!st2.empty()){
            ans.push_back(st2.top());
            st2.pop();
        }
    }
    vector<int> postorder(Node* root) {
         vector<int> ans;
        if(root==NULL){
            return ans;
        }
        stack<Node*> st;
        postorder(root,st,ans);
        return ans;
    }
};

思路：这样的输出结果就必须要添加一个变量来存储层数。树的结构体中是没有层数这个变量的。所以不能在结构体中添加。是用队列还是栈还是vector呢？最后反正要传给vector<vector<int>>型。《算法笔记》中的思路是如果要加上层数，那么就在树的结构体中添加个变量。但是在leetcode中这样的思路显然不可以。如何确定每层有多少个结点？

想不出来了，直接看评论区的代码。这也是把自己的思路的代码实现。这也是最直接的想法了。还待继续优化。

把评论区中的代码，边敲边写上注释，这样才能变成自己的东西，不然写了之后忘了，依旧啥也收获不到。

先写这一种方法。评论里还有以空间换时间，递归，BFS等实现。

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    vector<vector<int>> levelOrder(Node* root) {
        vector<vector<int>> res;
        if(!root) return res;
        queue<Node*> q;q.push(root);//队列是Node* 型的
        while(!q.empty()){
            int n=q.size();//获得队列里的所有元素(队列里的元素就是)
            vector<int> temp;//存储临时int型的vector；存放的是每层的队列的Node* 型所指向的val
            for(int i=0;i<n;i++){
                Node* node=q.front();q.pop();
                temp.push_back(node->val);
                vector<Node*> child=node->children;//这里是指向q队列中处于首位的结点的孩子结点
                for(int j=0;j<child.size();j++){//把孩子结点进入队列
                    q.push(child[j]);
                }
            }
            res.push_back(temp);//把存放的每层的元素的val，赋值给res
        }
        return res;
    }
};

参考的自己博客园的笔记里的思路。

递归法：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> vec;
        if(!root) return vec;
        else{
            visit(root,vec);
        }
        return vec;
    }
    void visit(TreeNode* root,vector<int> &vec){//这里的&必须加上，不然什么都不会输出！
        if(root!=NULL){
            vec.push_back(root->val);
            visit(root->left,vec);
            visit(root->right,vec);
        }
    }
};

把二叉树和N叉树的前序遍历的递归代码对比起来看一下：

N叉树：二叉树：

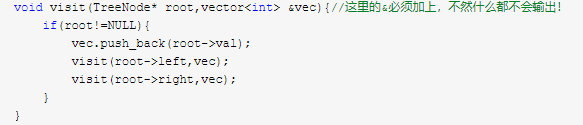
《实验楼》:

题解1 - 递归

面试时不推荐递归这种做法。

递归版很好理解，首先判断当前节点(根节点)是否为null，是则返回空vector，否则先返回当前节点的值，然后对当前节点的左节点递归，最后对当前节点的右节点递归。递归时对返回结果的处理方式不同可进一步细分为遍历和分治两种方法。

上述自己写的就是遍历法。

分治法如下，不太理解：

先把insert()方法掌握，这里用到第三个

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        if(root!=NULL){
            //Divide
            vector<int> l=preorderTraversal(root->left);
            vector<int> r=preorderTraversal(root->right);
            
            //Merge
            result.push_back(root->val);
            result.insert(result.end(),l.begin(),l.end());
            result.insert(result.end(),r.begin(),r.end());
        }
      return result;  
    }       
};

源码分析

使用遍历的方法保存递归返回结果需要使用辅助递归函数traverse，将结果作为参数传入递归函数中，传值时注意应使用vector的引用。分治方法首先分开计算各结果，最后合并到最终结果中。 C++ 中由于是使用vector, 将新的vector插入另一vector不能再使用push_back, 而应该使用insert。 Java 中使用addAll方法.

非递归实现：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> stk;
        if(root!=NULL){
            stk.push(root);
        }
        while(!stk.empty()){
            TreeNode* v=stk.top();stk.pop();
            if(v!=NULL&&v->val!=NULL){
                result.push_back(v->val);
            }
            if(v!=NULL&&v->left!=NULL){//注意这里！这是错误答案！
                stk.push(v->left);
            }
            else{
                if(v!=NULL&&v->right!=NULL){
                    stk.push(v->right);
                }
            }
        }
        return result;
    }       
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> stk;
        if(root!=NULL){
            stk.push(root);
        }
        while(!stk.empty()){
            TreeNode* v=stk.top();stk.pop();
            if(v!=NULL&&v->val!=NULL){
                result.push_back(v->val);
            }
            if(v->right!=NULL){//正确答案！
                stk.push(v->right);
            }
            if(v->left!=NULL){
                    stk.push(v->left);
            }
        }
        return result;
    }       
};

对比一下:

错误答案是先把左子树入栈，而正确答案是先把右子树入栈。

源码分析

对root进行异常处理
将root压入栈
循环终止条件为栈s为空，所有元素均已处理完
访问当前栈顶元素(首先取出栈顶元素，随后pop掉栈顶元素)并存入最终结果
将右、左节点分别压入栈内，以便取元素时为先左后右。
返回最终结果

其中步骤4,5,6为迭代的核心，对应前序遍历「根左右」。

所以说到底，使用迭代，只不过是另外一种形式的递归。使用递归的思想去理解遍历问题会容易理解许多。

递归的迭代法：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> v;
        if(root==NULL) return v;
        inorder(root,v);
        return v;
    }
    void inorder(TreeNode* root ,vector<int> &v){
        if(root->left!=NULL){
            inorder(root->left,v);
        }
        v.push_back(root->val);
        if(root->right!=NULL){
            inorder(root->right,v);
        }
    }
    
};

非递归：

分析：如果是中序遍历的话，那就不能直接把root结点入栈了，先要把root->left入栈。那么入栈顺序就是先根后右子节点。那么现在面临的一个问题就是如何用临时变量来存储根节点？（看过了教材中的算法后，其实不用临时变量来存储根节点，直接把根节点压入栈中即可，详细见下图）

感觉前序遍历最简单，中序和后序中等，层序最难。

自己实在是想不出来了！

中序遍历非递归实现的算法在课本上找到了！而且《实验楼》的算法和这个算法一模一样。务必要掌握！太重要啦！

算法思想：从根节点开始，只要当前节点存在，或者栈不空，则重复下面操作。

1.如果当前结点存在，则进栈并遍历左子树

2.否则退栈并访问，然后遍历右子树。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        stack<TreeNode*> stk;
        vector<int> vec;
        while(root!=NULL||!stk.empty()){
            if(root!=NULL){//根节点进栈，遍历左子树
                stk.push(root);
                root=root->left;
            }
            else{//根节点退栈，访问根节点，遍历右子树
                root=stk.top(); stk.pop();
                vec.push_back(root->val);
                root=root->right;
            }
        }
        return vec;
        
    }
    
};

递归法：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
         vector<int> v;
        if(root==NULL) return v;
        postorder(root,v);
        return v;
    }
    void postorder(TreeNode* root ,vector<int> &v){
        if(root->left!=NULL){
            postorder(root->left,v);
        }
        if(root->right!=NULL){
            postorder(root->right,v);
        }
        v.push_back(root->val);
        
    }
};

迭代法：

算法参考的是课本。但目前看似明白，但自己还是写不出来。

将递归写成迭代的难点在于如何在迭代中体现递归本质及边界条件的确立，可使用简单示例和纸上画出栈调用图辅助分析。

好像终于理解迭代和递归的关系了。迭代是必须把递归中的边界和条件一一列出，而递归是抽象化的迭代。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        TreeNode* p;
        TreeNode* q;
        vector<int> vec;
        stack<TreeNode*> stk;
        q=NULL;
        p=root;
        while(p!=NULL||!stk.empty()){
            if(p!=NULL){
                stk.push(p);p=p->left;//遍历左子树
            }
            else{
                p=stk.top();
                if((p->right==NULL)||(p->right==q)){//无右子树，或右子树已遍历过
                    vec.push_back(p->val);//访问根节点
                    q=p;
                    stk.pop();
                    p=NULL;
                }
                else{
                    p=p->right;
                }
            }
        }
        return vec;
    }       
};

还有一个方法是反转先序遍历。但是我觉得用分治算法也能解这个题。对同样的算法用在左子树和右子树中，最后把生成的结果按照左右根连接起来即可。

题解 - 使用队列

此题为广搜的基础题，使用一个队列保存每层的节点即可。出队和将子节点入队的实现使用 for 循环，将每一轮的节点输出。

跟N叉树的层序遍历代码差不多。只改进了一点。

代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        if(!root) return res;
        queue<TreeNode*> q;q.push(root);//队列是Node* 型的
        while(!q.empty()){
            int n=q.size();//获得队列里的所有元素(队列里的元素就是)
            vector<int> temp;//存储临时int型的vector；存放的是每层的队列的Node* 型所指向的val
            for(int i=0;i<n;i++){
                TreeNode* node=q.front();q.pop();
                temp.push_back(node->val);
                TreeNode* lchild=node->left;//这里是指向q队列中处于首位的结点的孩子结点
                if(node->left!=NULL) q.push(node->left);
                TreeNode* rchild=node->right;
                if(node->right!=NULL) q.push(node->right);
                /*for(int j=0;j<child.size();j++){//把孩子结点进入队列
                    q.push(child[j]);
                }*/
            }
            res.push_back(temp);//把存放的每层的元素的val，赋值给res
        }
        return res;
    }
};

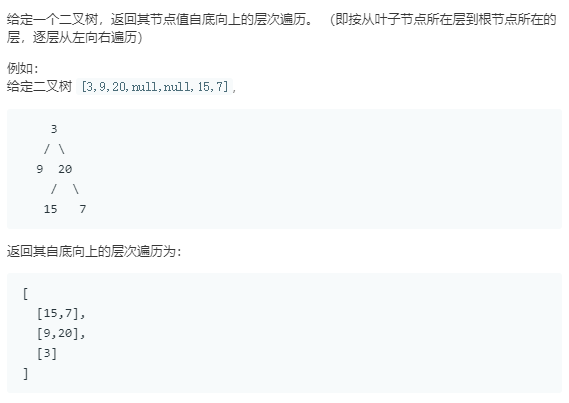
是自己想复杂了。自己想的是：把元素一个个入栈，最后出栈的时候必须要知道这一层的层数，但是在如何获取层数的时候卡住了。

但看了《实验楼》的思路后，发现真他妈简单。不是把元素入栈，是把vector<>型入栈，这样就很好做了。只是加了一个辅助栈就解决了问题。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
         vector<vector<int>> res;
        if(!root) return res;
        stack<vector<int>> stk;
        queue<TreeNode*> q;q.push(root);//队列是Node* 型的
        while(!q.empty()){
            int n=q.size();//获得队列里的所有元素(队列里的元素就是)
            vector<int> temp;//存储临时int型的vector；存放的是每层的队列的Node* 型所指向的val
            for(int i=0;i<n;i++){
                TreeNode* node=q.front();q.pop();
                temp.push_back(node->val);
                TreeNode* lchild=node->left;//这里是指向q队列中处于首位的结点的孩子结点
                if(node->left!=NULL) q.push(node->left);
                TreeNode* rchild=node->right;
                if(node->right!=NULL) q.push(node->right);
                /*for(int j=0;j<child.size();j++){//把孩子结点进入队列
                    q.push(child[j]);
                }*/
            }
            stk.push(temp);
        }
        while(!stk.empty()){
            res.push_back(stk.top());
            stk.pop();
        }
        return res;
    }
};

题解

此题在普通的 BFS 基础上增加了逆序输出，简单的实现可以使用辅助栈或者最后对结果逆序。

一开始的思路是:用先序遍历看一下总共有多少个元素。然后再用数学递推式log 算出来是第几层。

这样的想法后来发现是错误的。因为你不知道每层的有多少个元素。

应该用递归和迭代的方法来计算。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {//先获取先序遍历的数组
        if(root==NULL)
            return 0;
        int leftDepth=maxDepth(root->left);
        int rightDepth=maxDepth(root->right);
        return max(leftDepth,rightDepth)+1;
    }
};

需要用到求解最大深度的代码。

发现自己的一个问题：为啥一上来就想不到用递归来解决题目。只要可以利用层层递进的关系都可以用递归的！

所以自己一上来就把问题想的很复杂。

借鉴的评论区的代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isBalanced(TreeNode* root) {//判断根结点的左右孩子是否平衡
        if(!root)
            return true;
        if(abs(countFloor(root->left)-countFloor(root->right))>1)
            return false;
        else{
            if(isBalanced(root->left)&&isBalanced(root->right)){//判断左右孩子作为根节点的左右孩子是否是平衡树
                return true;
            }
            else return false;
        }
    }
    int countFloor(TreeNode* root){
        if(!root)
            return 0;
        return 1+max(countFloor(root->left),countFloor(root->right));
    }
};

好评论（如何写递归函数）：http://39.96.217.32/blog/4

下面我再列举几道我在刷题过程中遇到的也是用这个套路秒的题，真的太多了，大部分链表和树的递归题都能这么秒，因为树和链表天生就是适合递归的结构。

例3：平衡二叉树

相信经过以上2道题，你已经大概理解了这个模版的解题流程了。

那么请你先不看以下部分，尝试解决一下这道easy难度的Leetcode题（个人觉得此题比上面的medium难度要难）：Leetcode 110. 平衡二叉树

我觉得这个题真的是集合了模版的精髓所在，下面套三部曲模版：

找终止条件。 什么情况下递归应该终止？自然是子树为空的时候，空树自然是平衡二叉树了。
应该返回什么信息：

为什么我说这个题是集合了模版精髓？正是因为此题的返回值。要知道我们搞这么多花里胡哨的，都是为了能写出正确的递归函数，因此在解这个题的时候，我们就需要思考，我们到底希望返回什么值？

何为平衡二叉树？平衡二叉树即左右两棵子树高度差不大于1的二叉树。而对于一颗树，它是一个平衡二叉树需要满足三个条件：它的左子树是平衡二叉树，它的右子树是平衡二叉树，它的左右子树的高度差不大于1。换句话说：如果它的左子树或右子树不是平衡二叉树，或者它的左右子树高度差大于1，那么它就不是平衡二叉树。

而在我们眼里，这颗二叉树就3个节点：root、left、right。那么我们应该返回什么呢？如果返回一个当前树是否是平衡二叉树的boolean类型的值，那么我只知道left和right这两棵树是否是平衡二叉树，无法得出left和right的高度差是否不大于1，自然也就无法得出root这棵树是否是平衡二叉树了。而如果我返回的是一个平衡二叉树的高度的int类型的值，那么我就只知道两棵树的高度，但无法知道这两棵树是不是平衡二叉树，自然也就没法判断root这棵树是不是平衡二叉树了。

一些可以用这个套路解决的题

暂时就写这么多啦，作为一个高考语文及格分，大学又学了工科的人，表述能力实在差因此啰啰嗦嗦写了一大堆，希望大家能理解这个很好用的套路。

我会随时补充，正好大家可以看了上面三个题后可以拿这些题来练练手，看看自己是否能独立快速准确的写出递归解法了。

Leetcode 101. 对称二叉树

Leetcode 111. 二叉树的最小深度

Leetcode 226. 翻转二叉树：这个题的备注是最骚的。Mac OS下载神器homebrew的大佬作者去面试谷歌，没做出来这道算法题，然后被谷歌面试官怼了：”我们90％的工程师使用您编写的软件(Homebrew)，但是您却无法在面试时在白板上写出翻转二叉树这道题，这太糟糕了。”

Leetcode 617. 合并二叉树

Leetcode 654. 最大二叉树

Leetcode 83. 删除排序链表中的重复元素

Leetcode 206. 翻转链表

哇哇哇哇哇！自己看完了上篇的递归讲解自己写出来的！真爽！秒了！

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(!root) return NULL;//递归终止条件
        //本层该做的事情有：置换左右子树的指针
        reverse(root);
        
        //返回给上一层的是：
        return root;
    }
    TreeNode* reverse(TreeNode* root){
        if(!root) return NULL;
        if(root->left||root->right){//既有左子树又有右子树时
            TreeNode* temp=root->right;
            root->right=root->left;
            root->left=temp;
        }
        reverse(root->left);
        reverse(root->right);
        return root;
    }
};

又刷了一道递归题目

自己写了一些出错了，又借鉴的评论

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {//把右边的树合并到左边
        //递归终止条件
        if(t1==NULL&&t2==NULL) return NULL;
        //本层所要干的事情：
        TreeNode* root=new TreeNode(0);
        if(t1)
            root->val += t1->val;
        if(t2)
            root->val += t2->val;
        root->left=mergeTrees(t1?t1->left:0,t2?t2->left:0);
        root->right=mergeTrees(t1?t1->right:0,t2?t2->right:0);
        
        //返回值：
        return root;
    }
};

参考的评论代码。最终的递归终止条件要理解一下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return construct(0,0,nums.size()-1,nums);
        
    }
    TreeNode* construct(TreeNode* root,int left,int right,vector<int>& nums){
        //终止条件：为啥是left>right呢？ 仔细想一下会发现：当mid左边没有元素时，left和mid都是0，而此时mid-1就为-1.所以0>-1时是代表左边没有元素。
        if(left>right) return nullptr;
        //本层所要干的事情：
        int mid=left,max=INT_MIN; //初始化mid中间结点，和记录最大值的max（INT_MIN代表最小整数)
        for(int i=left;i<=right;i++){
            if(nums[i]>max){
                mid=i;
                max=nums[i];
            }
        }
        root=new TreeNode(nums[mid]);
        root->left=construct(root->left,left,mid-1,nums);
        root->right=construct(root->right,mid+1,right,nums);
        return root;
    }
};

这个题的最后返回值需要注意：

自己写的代码提交时就是因为返回值没有注意出现了bug，其实也是提交后才发现这里需要注意。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        //递归终止条件：
        if(root==NULL) return 0;
        //本层该做的事情：求左子树和右子树的深度
        int left=minDepth(root->left);
        int right=minDepth(root->right);
        //返回值(有两种情况，为了避免[1,2]这种情况的bug，因为[1,2]这种情况在本题中算2)
        if(left&&right)
            return min(left,right)+1;
        else return 1+left+right;
    }
};

还是递归！今天训练递归已经4，5道题目了。舒服

自己的思路是定义一个 static int 变量，但是结果总是数组中全部的数的和，可能是因为每次递归调用自己时候初始化的 int变量都为0。

于是参考了评论，发现不用创建int型变量就可以。

代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int rangeSumBST(TreeNode* root, int L, int R) {
        //终止条件：
        if(root==NULL) return 0;
        //本层该做的事情：
        if(root->val>R){
            return rangeSumBST(root->left,L,R);
        }
        if(root->val<L){
            return rangeSumBST(root->right,L,R);
        }
        else
            return root->val+rangeSumBST(root->left,L,R)+rangeSumBST(root->right,L,R);
            
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int d,m,n;
    int minDiffInBST(TreeNode* root) {
        //递归终止条件:
        if(root==NULL) return 100;
        //本层该做的:
        if(root->left||root->right){
            if(root->left&&root->right){
                d=min(abs(root->val-root->left->val),abs(root->val-root->right->val));
            }
            if(root->left&&root->right==NULL){
                d=abs(root->val-root->left->val);
            }
            if(root->left==NULL&&root->right){
                d=abs(root->val-root->right->val);
            }
        }
        m=minDiffInBST(root->left);
        n=minDiffInBST(root->right);
        //返回值：
        return min(min(d,m),n);
    }
};

感觉自己的改一下也没错。

借鉴的评论：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    //preVal是当前正在访问节点在中序遍历结果中前一个元素的值
    int preVal=-100,minRes=100;
    int minDiffInBST(TreeNode* root) {
       if(root==NULL)
           return minRes;
        //中序遍历的递归法：
        minDiffInBST(root->left);//先左子树
        minRes=min(minRes,root->val-preVal);//更新最小距离
        preVal=root->val;//更新中序遍历前一个元素的值
        minDiffInBST(root->right);//后右子树
        return minRes;
    }
};

还有迭代法。

自己的错误代码在注释中，其实思路没问题。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    //int val;
    bool isUnivalTree(TreeNode* root) {
        //递归终止条件
        if(root==NULL) return true;
        if(root->left&&root->val!=root->left->val) return false;
        if(root->right&&root->val!=root->right->val) return false;
        return isUnivalTree(root->left)&&isUnivalTree(root->right);
        
        /*自己的错误代码
        //本层要干的事情：
        val=root->val;
        if(!root->left&&!root->right) return true;
        if(root->left&&root->left->val==val) return true;这里错了！！！
        if(root->right&&root->right->val==val)  return true;这里错了！！！
        else return false;这里错了！！！
        //递归返回
        return(isUnivalTree(root)&&isUnivalTree(root->left)&&isUnivalTree(root->right));
        */
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isUnivalTree(TreeNode* root) {
        if(root==NULL) return true;
        if(!root->left&&!root->right) return true;
        if(root->left&&root->left->val!=root->val) return false;//这样才正确！！！
        if(root->right&&root->right->val!=root->val)  return false;//这样才正确！！！
        //递归返回
        return(isUnivalTree(root->left)&&isUnivalTree(root->right));
    }
};

非递归实现（前序遍历队列实现）：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int val;
    bool isUnivalTree(TreeNode* root) {
        if(root==nullptr) return true;
        int val = root->val;
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty()){
            TreeNode* tmp=q.front();
            q.pop();
            if(tmp->val!=val) return false;
            if(tmp->left!=nullptr) q.push(tmp->left);
            if(tmp->right!=nullptr) q.push(tmp->right);
        }
        return true;
    }
};

思路：根据给定的vector<int>，创建二叉搜索树。

评论的思路：递归解决。用new 方法递归创建二叉树，重点在于找到大于根节点的值的下标，就可以确定左右子树，在进行递归操作（要判断是否有右子树，不热会执行右子树的操作，返回一个None）

二叉搜索树中的先序遍历，要按照节点的val的大小顺序可以找到右子树，因为是按照升序排列。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* bstFromPreorder(vector<int>& preorder) {
        return helper(preorder,0,preorder.size()-1);
    }
    TreeNode* helper(vector<int>& preorder,int left,int right){//递归解决
        //递归条件：当没有元素时，此时0>-1,返回NULL
        if(left>right) return NULL;
        //本层所作的事情：
        TreeNode* root=new TreeNode(preorder[left]);
        int l=left+1;
        //查找根节点的右节点，找到就推出循环.
        for(;l<=right;l++){
            if(preorder[l]>preorder[left]) break;
        }
        root->left=helper(preorder,left+1,l-1);
        root->right=helper(preorder,l,right);
        return root;
    }
};

自己写出的。

递归：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        //递归终止条件：
        if(!root) return NULL;
        //本层要干的事情：
        if(root->val==val) return root;
        if(root->val<val&&root->right) return searchBST(root->right,val);
        if(root->val>val&&root->left) return searchBST(root->left,val);
        else return NULL;
    }
};

自己想复杂了。其实还是与上面的题意义。递归分治。与1008的思想相同，都是递归分治。

代码摘自评论，

注意以后求中间节点要用 mid=left + (right - left) /2 。为了避免溢出。

代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return sort(nums,0,nums.size()-1);
        }
    TreeNode* sort(vector<int>& nums,int left,int right){
        if(left>right) return NULL;
        int mid=left+(right-left)/2;
        TreeNode* root=new TreeNode(nums[mid]);
        root->left=sort(nums,left,mid-1);
        root->right=sort(nums,mid+1,right);
        return root;
    }
};
        
        /*理解错误，这个代码是小于val的一直往左，大于val的一直往右。这样只保证了对根节点而言是平衡二叉树，但平衡二叉树的定义是对每个节点的两个子树的高度差的绝对值不超过1！
        没理解清楚平衡二叉树的定义导致的！注意是对每个节点而言的！！！！
        if(nums.empty()) return NULL;
        int size=(nums.size()/2);
        stack<int> stk1;
        queue<int> stk2;
        TreeNode* root1= new TreeNode(nums[size]);
        TreeNode* temp=root1;
        TreeNode* root2=root1;
        for(int i=0;i<size;i++){
            stk1.push(nums[i]);
        }
        for(int j=(size+1);j<nums.size();j++){
            stk2.push(nums[j]);
        }
        while(!stk1.empty()||!stk2.empty()){
            if(!stk1.empty()){
                TreeNode* left=new TreeNode(stk1.top());
                stk1.pop();
                root1->left=left;
                root1=left;
            }
            if(!stk2.empty()){
                TreeNode* right=new TreeNode(stk2.front());
                stk2.pop();
                root2->right=right;
                root2=right;
            }
        }
        return temp;*/

想复杂了。其实还是递归就可以解决！简简单单几行代码。为啥递归能解决的问题老是想复杂？就不能好好想一下递归？

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int sum) {
        if(root==nullptr){
            return false;
        }
        if(!root->left&& !root->right){
            return root->val==sum;
        }
        return hasPathSum(root->left,sum-root->val)||hasPathSum(root->right,sum-root->val);
        
    }
};

思路没错，但就是有些问题，所以看了评论的代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return Symmetric(root,root);
    }
    bool Symmetric(TreeNode* p,TreeNode* q){
        //递归终止条件
        if(!q&&!p)
            return true;
        if(!p||!q)
            return false;
        //既有左子树和右子树的时候
        if(p->val==q->val){
            return Symmetric(p->left,q->right)&&Symmetric(p->right,q->left);
        }
        else//也就是(p->val!=q->val)时
           return false;
    }   
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return Symmetric(root,root);
    }
    bool Symmetric(TreeNode* p,TreeNode* q){
        //递归边界:
        if(!q&&!p) return true;//两个都为空时返回true
        if((!q&&p)||(!p&&q)) return false;//两个有一个空，一个非空时返回false
        //两个都为非空时,如果两个指针所指向的节点的值相等
        if(q->val==p->val){
            return Symmetric(q->left,p->right)&&Symmetric(q->right,p->left);
        }
        else return false;
        
    }   
};

迭代：(队列实现）

自己的思路是把左右子树分别入栈，再一个一个对比，可是没有实现。这个队列的是借鉴的评论

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(!root) return true;
        queue<TreeNode*> q;
        q.push(root->left);
        q.push(root->right);
        while(!q.empty()){
            TreeNode* left=q.front();q.pop();
            TreeNode* right=q.front();q.pop();
            if(left==NULL&&right==NULL) continue;
            if(!left||!right) return false;
            if(left->val!=right->val) return false;
            q.push(left->left);
            q.push(right->right);
            q.push(left->right);
            q.push(right->left);
        }
        return true;
        
    }   
};

利用好二叉搜索树的性质，不然没法进行递归。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* temp=NULL;
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        lowest(root,p,q);
        return temp;
    }
    void lowest(TreeNode* root,TreeNode* p,TreeNode* q){
        if(((root->val-p->val)*(root->val-q->val))<=0){
            temp=root;
        }
        else if((p->val<root->val)&&(q->val<root->val)){
            lowest(root->left,p,q);
        }
        else{
            lowest(root->right,p,q);
        }
    }
};

这题也是递归，只是需要点字符串的知识，需要构造一个函数，需要注意把xx类型转换成字符串的方法：to_string （xx);

看的评论；

需要自己再实现一遍！

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> res;
        if(root==NULL){
            return res;
        }
        string tmp="";
        func(res,tmp,root);
        return res;
    }
    void func(vector<string> &res,string tmp,TreeNode* root){
        //递归终止条件
        if(root->left==NULL&&root->right==NULL){
            tmp+=to_string(root->val);
            res.push_back(tmp);
            return;
        }
        tmp+=to_string(root->val);
        tmp+="->";
        if(root->left){
            func(res,tmp,root->left);
        }
        if(root->right){
            func(res,tmp,root->right);
        }
    }
};

https://blog.csdn.net/qq_41855420/article/details/89137353

解法1：先递归求中序遍历。利用二叉平衡树的中序遍历是有序的，再求最小差。

思路：先中序遍历（中序遍历的算法的递归写法一定要熟记在心），把遍历的结果放在vector<int>中，最后再从这个vector<int>里一个一个比较，最后返回最小的。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> result;
    int getMinimumDifference(TreeNode* root) {
        Inorder(root);
        int size=result.size(),mincount=INT_MAX;
        for(int i=1;i<size;i++){
            mincount=min(mincount,abs(result[i]-result[i-1]));
        }
        return mincount;
        
    }
    void Inorder(TreeNode* root){//中序遍历递归算法
        if(root==NULL) return;
        if(root->left){//先左子树
            Inorder(root->left);
        }
        result.push_back(root->val);//再根
        if(root->right){//最后右子树
            Inorder(root->right);
        }
    }
};

解法2：

先写好求二叉搜索树中最大值和最小值的函数，再用递归分别求每个子树的root 与root->right里的最大值的差的最小值和root->left和root的最小值作比较。递归进行，最后返回最小的min。

注意这里，对应着返回值中的“+root->val"。很重要！

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int findTilt(TreeNode* root){
        int sum=0;
        find(sum,root);
        return sum;
    }
   int find(int &sum,TreeNode* root){
       if(root==NULL) return 0;
       else{
           int rr=find(sum,root->right);
           int ll=find(sum,root->left);
           sum += abs(rr-ll);
           return rr+ll+root->val;//rr+ll+root->val中的"+root->val"很重要，一定要看懂！
       }
       /*自己的错误代码
       if(!root->left&&!root->right) return sum;
       if(!root->left) sum=abs(root->right->val);
       if(!root->right) sum=abs(root->left->val);
       else sum=abs(root->right->val-root->left->val);
       return find(sum,root)+find(sum,root->left)+find(sum,root->right);
       */
   }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p==NULL&&q==NULL) return true;
        if(p!=NULL&&q!=NULL&&p->val==q->val){
            return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
        }
        else return false;
    }
};

递归！

isSame函数判断树是否相同。这个函数比较重要

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSubtree(TreeNode* s, TreeNode* t) {
        if(s==NULL&&t==NULL){
            return true;
        }
        if(s!=NULL&&t!=NULL){
            if(s->val==t->val&&isSame(s,t)){
                return true;
            }
            if(isSubtree(s->left,t)){
                return true;
            }
            if(isSubtree(s->right,t)){
                return true;
            }
            else return false;
        }
        return false;
    }
    bool isSame(TreeNode* s,TreeNode* t){//这个结构要记住哦，出现很多次了
        if(s==NULL&&t==NULL){
            return true;
        }
        if(s!=NULL&&t!=NULL&&s->val==t->val){
            return isSame(s->left,t->left)&&isSame(s->right,t->right);
        }
        return false;
    }
};

这个题的难度在于，你有没有好好看一下这个N叉树的结构体。在结构体中透露了每层的节点个数有多少。利用这个性质进行递归就可以了。

获取children.size()就可以知道层中的节点个数。还需要一个int 型变量来记录一下当前的深度。

代码如下:

解法1：利用层序遍历递归

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    int maxDepth(Node* root) {
        if(root==NULL) return 0;
        int ans=0;
        int size=root->children.size();
        for(int i=0;i<size;i++){
            int t=maxDepth(root->children[i]);
            if(t>ans)
                ans=t;
        }
        return ans+1;
    }
};

简化版：

class Solution {
public:
    int maxDepth(Node* root) {
        if(root==NULL) return 0;
        int ans=0;
        int size=root->children.size();
        for(int i=0;i<size;i++){
            ans=max(ans,maxDepth(root->children[i]));
        }
        return ans+1;
    }
};

解法2：利用DFS

思路：

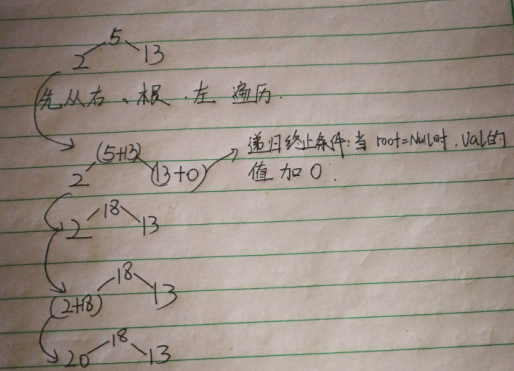
class Solution {
public:
    TreeNode* convertBST(TreeNode* root) {
        if(root==NULL) return NULL;
        Solve(root,0);
        return root;
    }
    int Solve(TreeNode* root,int sum){
        if(root==NULL) return sum;
        root->val += Solve(root->right,sum);
        return Solve(root->left,root->val);
    }
};

递归。重点在本层应该讨论的有几种情况：

代码如下：

class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        if(root==NULL||(root->left==NULL&&root->right==NULL)) return 0;
        if(root->left==NULL) return sumOfLeftLeaves(root->right);
        if(root->left->left==NULL&&root->left->right==NULL){
            return root->left->val+sumOfLeftLeaves(root->right);
        }
        return (sumOfLeftLeaves(root->left)+sumOfLeftLeaves(root->right));
    }
};

递归，思路是可以借助求最大深度的函数来求解此题。

class Solution {
public:
    int max=0;
    int diameterOfBinaryTree(TreeNode* root) {
        if(!root)
            return max;
        //TreeNode* p=root;
        if(root->left!=NULL || root->right!=NULL){
            max< depth(root->left)+depth(root->right)? max=depth(root->left)+depth(root->right):max=max;
        }
        diameterOfBinaryTree(root->left);
        diameterOfBinaryTree(root->right);
        return max;
        
    }
    int depth(TreeNode* r){
        if(!r)
            return 0;
        int left=depth(r->left);
        int right=depth(r->right);
        return left>right? left+1:right+1;
    }
};

更易于理解的版本：

class Solution {
public:
    int res=0;
    int diameterOfBinaryTree(TreeNode* root) {
        Solve(root);
        return res;
    }
    int Solve(TreeNode* root){
        if(root==NULL)
            return 0;
        int left=Solve(root->left);
        int right=Solve(root->right);
        res=max(res,left+right);
        return max(left,right)+1;
    }
};

查看全文

相关阅读:
Codeforces题目 java程序员
 5个能够有效帮助你快速创建超棒CSS3动画效果的类库 java程序员
 POJ3140:Contestants Division(DFS,树形DP) java程序员
 github的学习使用以及将自己开发的app传上去。
考研还是就业
 五月道别
 写给一个陌生的朋友
 有办法忘了一个人吗？
困惑啊,我倒底错在哪里?
招聘广告文字撰写者时注意11项

原文地址：https://www.cnblogs.com/JasonPeng1/p/12116568.html