Three Blocks Palindrome (hard version) CF

1. 题面

2. 题意

给你一个长度为n的序列，序列中的每个元素的范围为[1,200].让你求出它的最长回文子序列的长度（不要求子序列连续）。

其中本题定义的回文子序列满足如下要求：

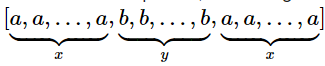
x,y>=0；a可以等于b。

3. 思路

二维树状数组+二分

由于题目强烈提示元素范围为[1,200]，因此我们可以用c[i][j]来存数字i在数组的前j个数中共有多少个。

然后我们开始遍历数组a，当我们遍历到第i个位置时，将前i个数中共有多少个a[i]赋值给cnt（通过树状数组求），然后二分查找位置res，使得a[res+1…n]中恰好有cnt个a[i].

①若不存在res，则用cnt去更新ans；

②若存在res，则暴力遍历1~200找到a[i+1…res]中数字最多出现的次数maxx，然后用2*cnt+maxx去更新ans。

 

4. 代码

#define _CRT_SECURE_NO_WARNINGS
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<map>
#include<vector>
#include<set>
#include<stack>
#include<queue>
#include<ctime>
using namespace std;
#define ll long long
#define ull unsigned long long
#define PI acos(-1)
#define lowbit(x) (x)&(-x)
#define lc rt<<1
#define rc rt<<1|1
#define pb push_back
#define pii pair<int,int>
const double eps = 1e-6;
const double Dlt = 0.97;
const int inf = 0x3f3f3f3f;
const ll INF = 1e18;
const int maxn = 200000 + 10;
const int maxm = 200 + 10;
const int mod = 2333333;
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
inline ll read() {
    char ch = getchar(); ll x = 0, f = 1;
    while (ch < '0' || ch>'9') { if (ch == '-')f = -1; ch = getchar(); }
    while ('0' <= ch && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
    return x * f;
}

int n;
int a[maxn];
int c[maxm][maxn];
void init() {
    for (int i = 1; i <= 200; ++i) {
        for (int j = 1; j <= n; ++j) {
            c[i][j] = 0;
        }
    }
}
void update(int pos, int x) {
    for (; x <= n; x += lowbit(x))c[pos][x] += 1;
}
int query(int pos, int x) {
    int res = 0;
    for (; x; x -= lowbit(x)) {
        res += c[pos][x];
    }
    return res;
}

int main() {
    int T = read();
    while (T--) {
        n = read();
        init();
        for (int i = 1; i <= n; ++i) {
            a[i] = read();
            update(a[i], i);
        }
        int ans = 0;
        for (int i = 1; i <= n; ++i) {
            int cnt = query(a[i], i);                      //求从1到i共有多少个a[i];
            ans = max(ans, cnt);
            int l = i, r = n;
            int res = inf;
            int tot = query(a[i], n);                     //第i个数在本数组中的数量
            while (l <= r) {                                 //二分找出临界点
                int mid = (l + r) >> 1;
                if (tot - query(a[i], mid) >= cnt) {
                    res = mid;
                    l = mid + 1;
                }
                else {
                    r = mid - 1;
                }
            }
            if (res == inf)continue;                    //表明未查找到存在后x个a
            int maxx = 0;
            for (int j = 1; j <= 200; ++j) {         //枚举(i,res]之间最多的元素个数
                maxx = max(maxx, query(j, res) - query(j, i));
            }
            ans = max(ans, maxx + 2 * cnt);
        }
        printf("%d
", ans);
    }
}