ACM-ICPC 2018 徐州赛区网络预赛 G. Trace

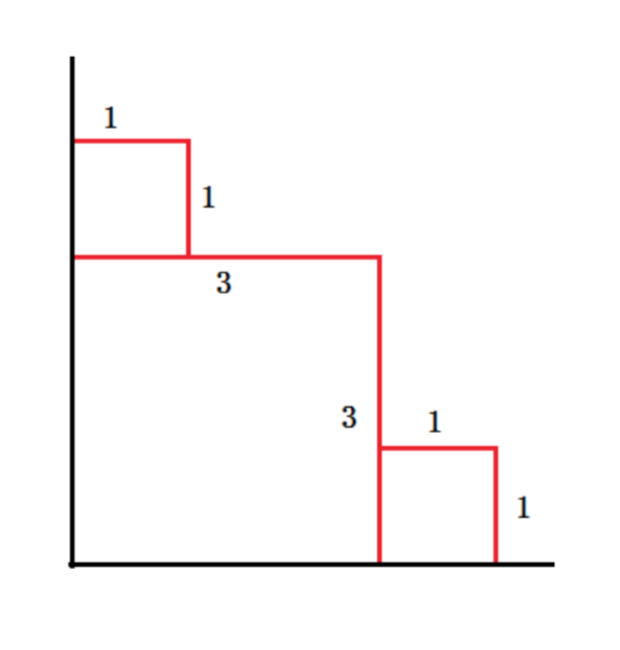
There's a beach in the first quadrant. And from time to time, there are sea waves. A wave ( xx , yy ) means the wave is a rectangle whose vertexes are ( 00 , 00 ), ( xx , 00 ), ( 00 , yy ), ( xx , yy ). Every time the wave will wash out the trace of former wave in its range and remain its own trace of ( xx , 00 ) -> ( xx , yy ) and ( 00 , yy ) -> ( xx , yy ). Now the toad on the coast wants to know the total length of trace on the coast after n waves. It's guaranteed that a wave will not cover the other completely.

Input

The first line is the number of waves n(n le 50000)n(n≤50000).

The next nn lines，each contains two numbers xx yy ,( 0 < x0<x , y le 10000000y≤10000000 )，the ii-th line means the ii-th second there comes a wave of ( xx , yy ), it's guaranteed that when 1 le i1≤i , j le nj≤n ，x_i le x_jxi​≤xj​ and y_i le y_jyi​≤yj​ don't set up at the same time.

Output

An Integer stands for the answer.

Hint：

As for the sample input, the answer is 3+3+1+1+1+1=103+3+1+1+1+1=10

样例输入复制

3
1 4
4 1
3 3

样例输出复制

10


题意：输入n代表有n波海浪，海浪会有一个范围，冲成一个矩形，会在边缘的地方留下痕迹，如果这波海浪碰到了之前留下来的痕迹，会把它的痕迹所冲掉，然后问最后总共留下来的痕迹有多少
注意；你后面的海浪不可能把之前的一波海浪全部覆盖

思路：首先我们肯定要倒着来访问
比赛时的想法：然后我开始没看到那句后面的不会把前面的浪全部冲掉那一句话，然后我的想法是给每个行列位置置一个浪冲的的最大范围，然后只要用那个最大的范围减中间差值即可
但是后面我写炸了，用的是线段树维护最大冲浪范围， 

赛后：我们仔细想想（后面的浪不会把之前的浪全部冲掉这一句话），所以我们只可能出现 （一个比x大，一个比y小），  （一个比x小，一个比y大）
我们倒着来，找最近的比他小的数即可，二分找来降低复杂度，

如果有比他小的 那么我们就+他们的差值

 

如果当前的坐标就是最小的，找不到的时候，那么我们的这个是最小，说明我们的另外一个坐标肯定比他们长，
比他们长的话就加当前长度即可（因为另一边肯定比他长，然后就露出去了）

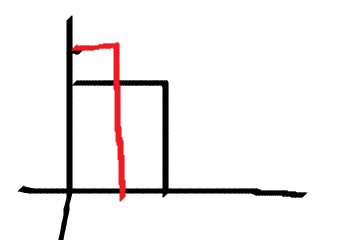
#include <bits/stdc++.h>
using namespace std;

long long gao(vector<int> vec) {
    int sz = vec.size();
    set<int>st;
    long long ans = 0;
    for (int i = sz-1; i >= 0; i--) {//倒着访问
        set<int>::iterator it = st.lower_bound(vec[i]);
        if (it == st.begin()) {//如果当前的坐标比所有的小，说明另一个肯定比他们大，所以加全部，图二
            ans += vec[i];
        } else {
            it--;
            ans += vec[i] - *it;//图一
        }
        st.insert(vec[i]);
    }
    return ans;
}
int main() {
    int n;
    while(scanf("%d", &n) == 1) {
        vector<int>vec1, vec2;
        int x,y;
        while(n--) {
            scanf("%d%d", &x, &y);
            vec1.push_back(x);
            vec2.push_back(y);
        }
        cout<<gao(vec1) + gao(vec2)<<endl;
    }
}