摘要,面试中问集合的时候是非常多的,最简单的莫过于ArrayList 和 LinkList区别了,难一点的可能会问集合中某一个方法的实现细节。
场景对话:面试官:问你一个关于集合的问题,ArrayList是有序的么?
我:不是
面试官:那怎么对它进行排序呢?
我:可以使用Collections.sort()方法,这个方法默认是升序的,如果要降序排列可以重写Compare方法或者使用reverseOrder();
如下:List<Integer> list = new ArrayList<>();
list.add(1);
list.add(2);
list.add(3);
Collections.sort(list);
Collections.sort(list,Collections.<Integer>reverseOrder()); or
Collections.sort(list, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
//降序
return o2.compareTo(o1);
}
});
面试官:那你知道他的底层是怎样实现的吗?
我:(这好像以前没事的时候看过一眼,不过没太在意) 额...这个..额 以前有看过,让我想想
(半分钟后)好吧 ,不太记得具体的实现的过程了,但是记得是基于归并排序实现的。
面试官:那你回去再看看吧,下一个问题...(鸡鸡)
源码:
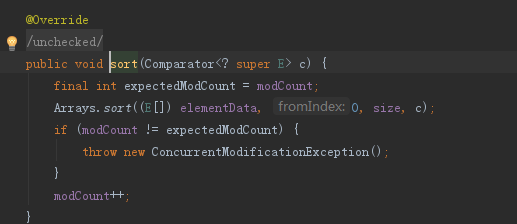
(这里可以看到 Collections.sort()是基于Arrays.sort()实现的 )
Array.sort()

TimSort.sort()
static <T> void sort(T[] a, int lo, int hi, Comparator<? super T> c,
T[] work, int workBase, int workLen) {
assert c != null && a != null && lo >= 0 && lo <= hi && hi <= a.length;
int nRemaining = hi - lo;
if (nRemaining < 2)
return; // array的大小为0或者1就不用排了
// 当数组大小小于MIN_MERGE(32)的时候,就用一个"mini-TimSort"的方法排序,jdk1.7新加
if (nRemaining < MIN_MERGE) {
int initRunLen = countRunAndMakeAscending(a, lo, hi, c);
binarySort(a, lo, hi, lo + initRunLen, c);
return;
}
//先扫描一次array,找到已经排好的序列,然后再用刚才的mini-TimSort,然后合并,这就是TimSort的核心思想
TimSort<T> ts = new TimSort<>(a, c, work, workBase, workLen);
int minRun = minRunLength(nRemaining);
do {
// Identify next run
int runLen = countRunAndMakeAscending(a, lo, hi, c);
// If run is short, extend to min(minRun, nRemaining)
if (runLen < minRun) {
int force = nRemaining <= minRun ? nRemaining : minRun;
binarySort(a, lo, lo + force, lo + runLen, c);
runLen = force;
}
// Push run onto pending-run stack, and maybe merge
ts.pushRun(lo, runLen);
ts.mergeCollapse();
// Advance to find next run
lo += runLen;
nRemaining -= runLen;
} while (nRemaining != 0);
// Merge all remaining runs to complete sort
assert lo == hi;
ts.mergeForceCollapse();
assert ts.stackSize == 1;
}
Array.sort()底层实现都是TimSort实现的,这是jdk1.7新增的,以前是归并排序。TimSort算法就是找到已经排好序数据的子序列,然后对剩余部分排序,然后合并起来