前言
这一节,请看前章。
通过前节,我们知道什么是二分法了。
那么问题就来了,前面二分法把中间值作为分值,那么这种效率是否高呢?
比如说1到100的一个数组,我需要找的是100,那么二分法要分很多次。
这时候我们需要找规律了,这是我们发现均匀分布的,那么是否可以通过比例的值来接近。
比如说把mid 设置成 mid=left+(right-left)*[(findval-arr[left])/arr[left]-arr[right]]
这样子就可以接近于正确值,也就是说每一次过滤的值越多。
正文
代码:
static int num;
static void Main(string[] args)
{
int[] arr = new int[100];
for (int i = 1; i <=100; i++)
{
arr[i - 1] = i;
}
List<int> list = binaryListSearch(arr, 0, arr.Length - 1, 100);
foreach (var u in list)
{
Console.WriteLine(u);
}
Console.WriteLine("一共多少次递归:"+num);
Console.ReadKey();
}
public static List<int> binaryListSearch(int[] arr, int left, int right, int findValue)
{
List<int> result = new List<int>();
int temp = binarySearch(arr, 0, arr.Length - 1, findValue);
if (temp != -1)
{
for (int i = 0; i <= temp - 1; i++)
{
if (arr[i] == arr[temp])
{
result.Add(i);
}
}
result.Add(temp);
for (int i = temp + 1; i < arr.Length; i++)
{
if (arr[i] == arr[temp])
{
result.Add(i);
}
}
}
return result;
}
public static int binarySearch(int[] arr, int left, int right, int findValue)
{
num++;
//表示没有找到
if (left > right)
{
return -1;
}
int mid = left + (right - left) * ((findValue - arr[left]) / (arr[right] - arr[left]));
if (findValue > arr[mid])
{
return binarySearch(arr, mid + 1, right, findValue);
}
else if (findValue < arr[mid])
{
return binarySearch(arr, left, mid - 1, findValue);
}
else
{
return mid;
}
}
结果:
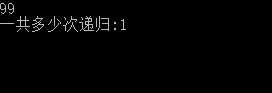
可以看出效率大大提高,所以我们也应该适当的调一调参数。