C++实现__搜索二叉树

1、搜索二叉树的概念

　　搜索二叉树又叫二叉排序树，它 或是 一颗空树，或是 一颗具有特殊性质的树

　　特殊性质：

　　　　1>若它的左子树不为空，则左子树上所有结点的值都小于其双亲结点的值

　　　　2>若它的右子树不为空，则右子树上所有结点的值都大于其双亲结点的值

　　　　3>它的左右子树也分别是二叉搜索树

　　搜索二叉树的数据存储方式是以中序遍历排序存储的

2、搜索二叉树的操作及图解

　　查找操作 、 插入操作、删除操作

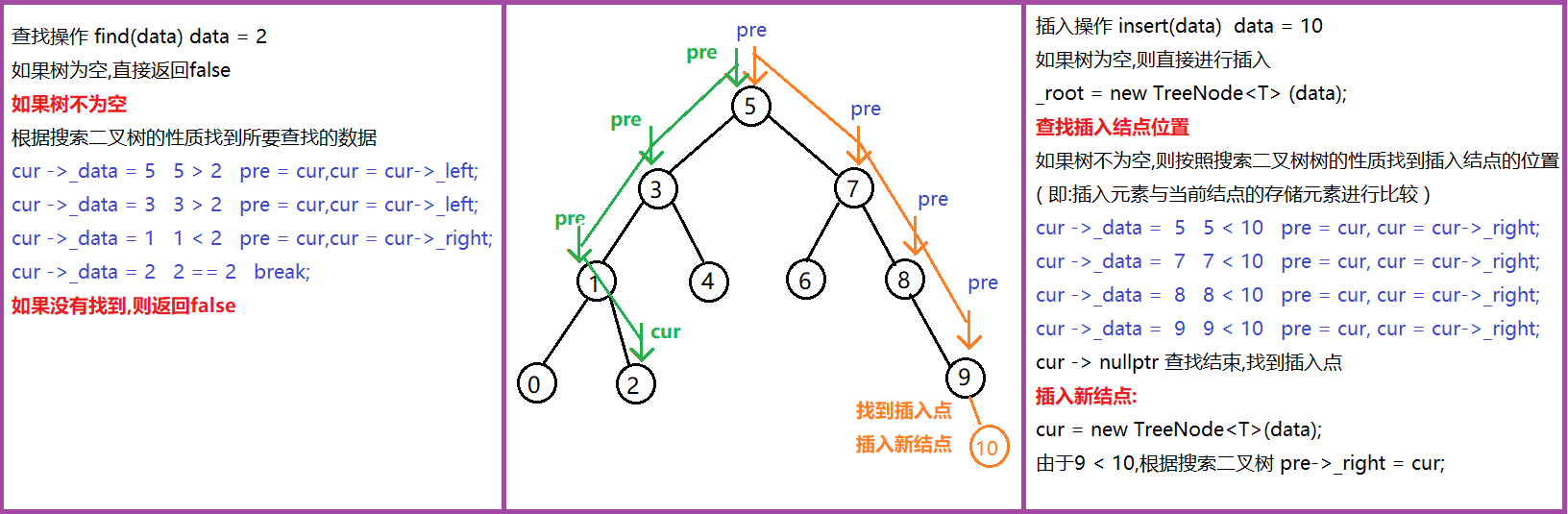
　插入、查找操作

　　删除操作

　 　　 如果树为空，直接返回false
　　　如果树不为空，先查找删除结点
　　　若删除结点不存在，返回false
　　　若存在，需进行分况讨论
　　　　1、左右子树都存在的情况
　　　　2、只有左子树，可以直接进行删除
　　　　3、只有右子树或没有左右子树,可以直接进行删除

　　考虑特殊的删除情况：删除根结点

　　　　需要在之前的的操作上，添加判断是否删除根结点的语句，具体情况看下面代码

对于删除操作的左右子树都存在的情况下,赋值操作起来会更简单一点

方法:先找到最右结点,将其值赋给要删除的结点的值,然后释放掉最右结点--OK

只对左右子树都存在的情况进行操作说明:

if (cur->_left && cur->_right) {
　　TreeNode<T> * cur2 = cur->_left;
　　TreeNode<T> * pre2 = cur2;
　　for (; cur2->_right; pre2 = cur2, cur2 = cur2->_right);
　　cur->_data = cur2->_data;
　　pre->_right = cur2->left;

　　delete cur2;
}

3、搜索二叉树的实现

　　1>搜索二叉树的实现

template <class T>
class TreeNode{
　　T _data;
　　TreeNode<T>* _left;
　　TreeNode<T>* _right;
　　public:
　　TreeNode(const T& data = T()):
　　　　_data(data),
　　　　_left(nullptr),
　　　　_right(nullptr)
　　{}
　　template <class T>
　　friend class BinarySearchTree;
};
template <class T>
class BinarySearchTree {
    TreeNode<T> * _root;
public:
    // 初始化
    BinarySearchTree() :
        _root(nullptr)
    {}
    
    // 插入操作
    bool Insert(const T & data) {
        // 如果根为nullptr,直接插入
        if (_root == nullptr) {
            _root = new TreeNode<T>(data);
            return true;
        }
        // 如果根不为nullptr,遍历找到插入点
        TreeNode<T> * cur = _root;    // 记录查找的结点位置
        TreeNode<T> * pre = nullptr;    // 记录双亲的结点位置
        while (cur) {
            // 如果插入元素已存在,直接返回false
            if (cur->_data == data) {
                return false;
            }
            pre = cur;
            if (data < cur->_data ) {
                cur = cur->_left;
            }
            else {
                cur = cur->_right;
            }
        }
        cur = new TreeNode<T>(data);
        // data与双亲进行大小比较
        if (pre->_data > data)
            pre->_left = cur;
        else
            pre->_right = cur;
        return true;
    }
    
    // 删除操作
    bool Erase(const T & data) {
        // 判断树是否为空
        if (_root == nullptr)
            return false;
        TreeNode<T> * cur = _root;
        TreeNode<T> * pre = nullptr;
        // 遍历查找所要删除的结点
        while (cur) {
            pre = cur;
            if (data < cur->_data) {
                cur = cur->_left;
            }
            else if (data > cur->_data) {
                cur = cur->_right;
            }
            else {
                break;
            }
        }
        // 如果遍历到最后,cur == nullptr,说明不存在,直接返回false
        if (cur == nullptr)
            return false;
        // 删除结点需要分情况讨论
        // 1.左右孩子都存在
        if (cur->_left && cur->_right) {
            TreeNode<T> * cur2 = cur->_left;
            TreeNode<T> * pre2 = cur;
            // 直接往最右叶子结点查找
            if (cur2->_right) {
            for (; cur2->_right; pre2 = cur2, cur2 = cur2->_right);
                // 让pre2指向最右叶子结点的左孩子
                pre2->_right = cur2->_left;
                // cur2指向cur的左孩子结点
                cur2->_left = cur->_left;
            }
            // cur2指向cur的右孩子
            cur2->_right = cur->_right;
            // 考虑删除根结点的情况
            if(cur == pre)
                _root = cur2;
            else {
                // 判断cur是左孩子还是右孩子,将cur替换为cur2
                if (cur->_data < pre->_data)
                    pre->_left = cur2;
                else
                    pre->_right = cur2;
            }    
            // 释放掉cur结点
            delete cur;
        }
        else if (cur->_left) {
            if(cur == pre){
                _root = cur->_left;
            else{          
                if (cur->_data < pre->_data)
                    pre->_left = cur->_left;
                else
                    pre->_right = cur->_left;}
            }
            delete cur;
        }
        else {
            if(cur == pre)
                _root = cur->_right;
            else{
                if (cur->_data < pre->_data)
                    pre->_left = cur->_right;
                else
                    pre->_right = cur->_right;
        }            delete cur;
        }
        return true;
    }
    // 查找操作
    void Find(const T & data) {
        if (_root == nullptr)
            return;
        TreeNode<T> * cur = _root;
        while (cur) {
            if (data < cur->_data)
                cur = cur->_left;
            else if (data > cur->_data)
                cur = cur->_right;
            else
                break;
        }
        if (cur == nullptr) 
            return;
        cout << " cur->_data :" << cur->_data << endl;
        delete cur;
    }
};