目录
- 引入头结点:①统一第一个元素结点与其他结点的操作;②统一空表和非空表的处理。
顺序表
数组有上界和下界,数组的元素在上下界内是连续的。
存储10,20,30,40,50的数组的示意图如下:

数组的特点是:数据是连续的;随机访问速度快。
数组中稍微复杂一点的是多维数组和动态数组。对于C语言而言,多维数组本质上也是通过一维数组实现的。至于动态数组,是指数组的容量能动态增长的数组;对于C语言而言,若要提供动态数组,需要手动实现;而对于C++而言,STL提供了Vector;对于Java而言,Collection集合中提供了ArrayList和Vector。
链表
- 一般地插入和删除:都需要前一个结点。
题目:一个链表最常用的操作是在末尾插入结点(即 需要尾结点)和删除结点(即 需要尾的前驱),则选用“带头结点的双循环链表”最省时间。
题目:设对n个元素的线性表的运算只有4种:删除第一个元素(第一的前);删除最后一个元素(尾的前);在第一个元素之前插入新元素(第一的前);在最后一个元素之后插入新元素(尾),则最好使用“只有头结点指针没有尾结点指针的循环双链表”(这个链表满足前面所述所有条件)。
单向链表
单向链表(单链表)是链表的一种,它由节点组成,每个节点都包含下一个节点的指针。
单链表的示意图如下:
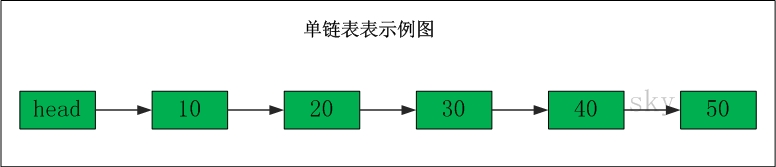
表头为空,表头的后继节点是"节点10"(数据为10的节点),"节点10"的后继节点是"节点20"(数据为10的节点),...单链表删除节点

删除"节点30"
删除之前:"节点20" 的后继节点为"节点30",而"节点30" 的后继节点为"节点40"。
删除之后:"节点20" 的后继节点为"节点40"。
//删除p之后的s
p->next = s->next;
free(s);- 单链表插入节点
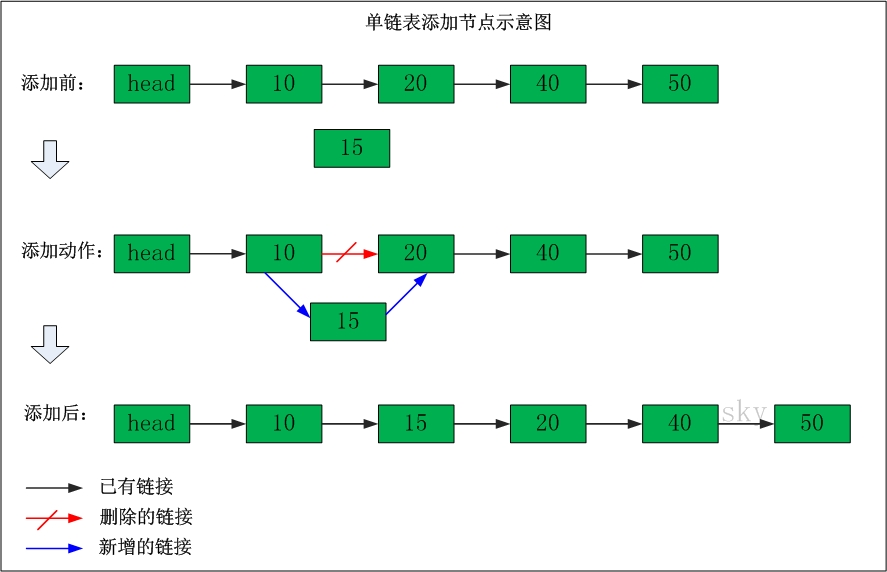
在"节点10"与"节点20"之间添加"节点15"
添加之前:"节点10" 的后继节点为"节点20"。
添加之后:"节点10" 的后继节点为"节点15",而"节点15" 的后继节点为"节点20"。
//在p之后插入s,确保不断链
s->next = p->next;
p->next = s;- 扩展:对某一节点进行前插操作
先后插,再交换前后数据,可等价为前插
//将s结点插入到p之前
s->next = p->next;
p->next = s;
swap(s->data,p->data);- 扩展:删除结点*p
将其后继结点的值赋予其自身,再删除p的后继结点
q = p->next;
p->data = p->next->data;
p->next = q->next;
free(q);- 单链表的特点是:节点的链接方向是单向的;相对于数组来说,单链表的的随机访问速度较慢,但是单链表删除/添加数据的效率很高。
双向链表
双向链表(双链表)是链表的一种。和单链表一样,双链表也是由节点组成,它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。一般我们都构造双向循环链表。
双链表的示意图如下:

表头为空,表头的后继节点为"节点10"(数据为10的节点);"节点10"的后继节点是"节点20"(数据为10的节点),"节点20"的前继节点是"节点10";"节点20"的后继节点是"节点30","节点30"的前继节点是"节点20";...;末尾节点的后继节点是表头。- 双链表删除节点:
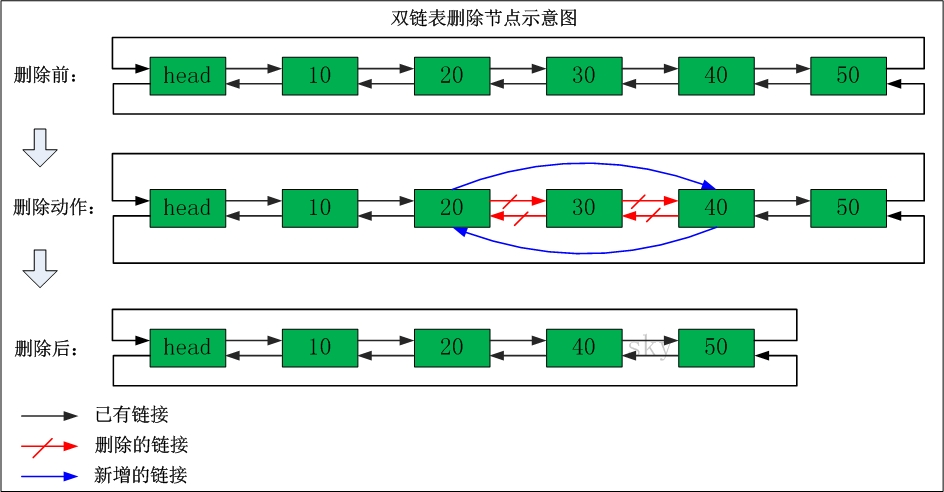
删除"节点30"
删除之前:"节点20"的后继节点为"节点30","节点30" 的前继节点为"节点20"。"节点30"的后继节点为"节点40","节点40" 的前继节点为"节点30"。
删除之后:"节点20"的后继节点为"节点40","节点40" 的前继节点为"节点20"。
//删除p之后的s
p->next = s->next;
s->next->prior = p;- 双链表插入节点:
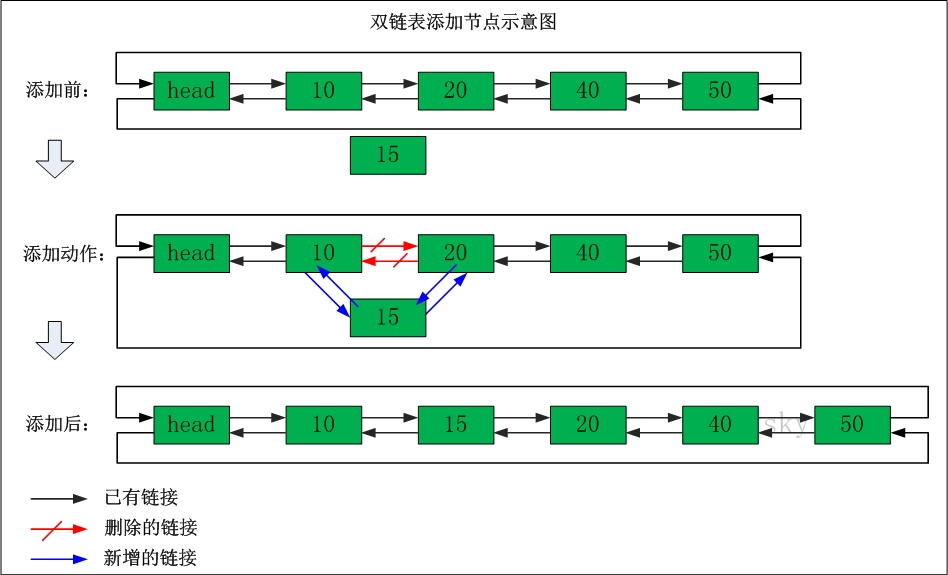
在"节点10"与"节点20"之间添加"节点15"
添加之前:"节点10"的后继节点为"节点20","节点20" 的前继节点为"节点10"。
添加之后:"节点10"的后继节点为"节点15","节点15" 的前继节点为"节点10"。"节点15"的后继节点为"节点20","节点20" 的前继节点为"节点15"。
//在p之后插入s,确保不断链
s->prior = p;
s->next = p->next;
s->prior->next = s;
s->next->prior = s;静态链表
静态链表借助数组来描述线性表的链式存储结构,结点也有数据域data和指针域next,与前面的链表的指针不同的是,这里的指针是结点的相对地址(数组下标),又称游标。和顺序表一样,静态链表也要预先分配一块连续的内存空间。

- 存储结构:
# define MaxSize 50 //静态链表的最大长度
typedef struct { //静态链表结构类型的定义
ElemType data; //存储数据元素
int next; //下一个元素的数组下标
}SLinkList[MaxSize];//Static- 静态链表以next==-1作为其结束的标志。
静态链表的插入、删除操作与动态链表的相同,只需要修改指针,而不需要移动元素。
总体来说,静态链表没有单链表使用起来方便,但在一些不支持指针的高级语言(如 Basic)中,这是一种非常巧妙的设计方法。
顺序表
注意:数组只是顺序表的实体表现,而不是就是顺序表。这是一个抽象和一个实体的关系。
- 存储结构:
#define MaxSize 50 //定义线性表的最大长度
typedef struct {
ElemType data[MaxSize]; //顺序表的元素
int length; //顺序表的当前长度
}SqList; //顺序表的类型定义常用算法
放过法
问题:对长度为n的顺序表L,编写一个时间复杂度为O(n)、空间复杂度为O(1)的算法,该算法删除线性表中所有值为x的数据元素。
- 算法:
bool deleteX(SqList &L, ElemType x) {
int k = 0; // 记录值不等于x的元素个数
for(int i=0; i<L.length; i++) {
if(L.data[i] != x) { // 如果不等于x,那就放你过,让你进入线性表(新)
L.data[k] = L.data[i];
k++;
}
}
L.length = k;
}逆置
- 算法:
//顺数第i个+倒数第i个=总长度n-1
void reverse(SqList &L) {
ElemType t;
for(int i = 0; i<L.length/2; i++) { // 依次交换前后元素
t = L.data[i];
L.data[i] = L.data[length-i-1];
L.data[length-i-1] = t;
}
}归并算法
链表
- 存储结构:
typedef struct LNode { //定义单链表结点类型
ElemType data; //数据域
struct LNode *next; //指针域
}LNode, *LinkList;常用算法
放过法
其实链表无需放过法,其插入和删除元素很方便,不需要移动元素。
问题:
在一个递增有序的线性表中,有数值相同的元素存在。若存储方式为单链表,设计算法去掉数值相同的元素,使表中不再有重复的元素。
- 设计思想:
由于是有序表,所有相同值域的结点都是相邻的,用p扫描递增单链表L,
若*p结点的值域等于其后继结点的值域,则删除后者,否则p移向下一个结点。 - 算法:
void deleteSame(LinkList &L) {
LNode *p = L->next, *q; //q是操作指针用来删除
if(p == NULL) {
return;
}
while(p->next != NULL) {
if(p->data == p->next->data) {
q = p->next; //赋值给q,删除p->next
p->next = q->next;
free(q);
}else {
p = p->next; //否则前进
}
}
}- 效率:
时间复杂度:O(n)
空间复杂度:O(1)
头插法(逆置)
生成后进先出的单链表(链式栈)
- 逆序(逆置):
q->next = head->next;
head->next = q;尾插法
- 顺序:
q->next = rear->next;
rear->next = q;
rear = q; //尾指针继续指向尾结点归并算法
两个已经有序的线性表,归并为一个有序的线性表。(两两比较取较小值放入新的有序线性表)
问题:已知两个链表A和B分别表示两个集合,其元素递增序列。编制函数,求A与B的交集,并存放于A链表中。
- 设计思想:
采用归并的思想,设置两个工作指针pa和pb,对两个链表进行归并扫描,只有同时出现在两集合中的元素才链接到结果表中且进保留一个,其他的结点全部释放。当一个遍历完毕后,释放另一个表剩下的全部结点。 - 算法:
LinkList same(LinkList &A, LinkList &B) {
LNode *pa = A->next, *pb = B->next, *q, *t = A; //q为操作指针,t为尾指针
A->next = NULL; //摘下头结点
while(pa && pb) {
if(pa->data == pb->data) {
q = pa;
pa = pa->next;
q->next = t->next; //将A集合那个元素插入到结果表中(尾插法)
t->next = q;
t = q; //尾插法必备
q = pb; //将B集合中相同的元素释放
pb = pb->next;
free(q); //这两个集合,每扫描一个元素就释放一个,所以每次都是释放第一个元素,无需前驱后继链接
}else if(pa->data < pb->data) { //如果pa中的元素值比较小,那么后移指针,找大一点的(这样才能与pb匹配)
q = pa;
pa = pa->next;
free(u);
}else {
q = pb;
pb = pb->next;
free(q);
}
}
//如果还有链表非空,释放剩下的部分
if(pb) {
pa = pb;
}
while(pa) {
q = pa;
pa = pa->next;
free(q);
}
free(B); //释放B表头结点
return A;
}- 效率:
时间复杂度:O(len1+len2) //while(pa && pb)
空间复杂度:O(1)
标尺法
找倒数第k个元素
- 设计思想:
MY:扫描链表所有结点,得到链表长度n;再从头扫描第n-k+1个结点后,即是倒数第k个,输出。 - 算法:
typedef int ElemType;
typedef struct LNode {
ElemType data;
struct LNode *link;
}LNode, *LinkList;
int searchK1(LinkList list, int k) {
LNode *p = list->link;
int length = 0;
int count = 0;
while(p) { //得到表长
length++;
p = p->link;
}
if(k<1 || k>length) { //合法性检验
return 0;
}
p = list->link;
while(p) { //寻找倒数第k个
count++;
if(count == length-k+1) {
printf("%d", p->data);
return 1;
}else {
p = p->link;
}
}
}- 标尺法:
int searchK2(LinkList list, int k) {
LNode *p = list->link, *q = list->link;
int count = 0;
while(p) { //找到第k个结点q(标尺长度为k)
count++;
if(count == k) {
break;
}else {
p = p->link;
}
}
if(!p) { //如果p不存在,即p遍历完了链表,没找到第k个
return 0;
}
while(p->next) { //同步后移 (走到头,由于标尺长度为k,所以q就是倒数第k个)
p = p->link;
q = q->link;
}
printf("%d", q->data);
return 1;
}- 效率:
时间复杂度:O(n)
空间复杂度:O(1)
同起共进法(同一起点共同前进)(共同后缀)
(同起共进法)共同后缀
问题:str1和str2两个链表,在后面一部分指向了同一条子链表,是公共的,要求出共同后缀。
- 设计思想:
- 分别求出str1和str2所指的两个链表长度m和n。
- 将两个链表以表尾对齐:令指针p、q分别指向str1和str2的头结点,
若m≥n,则指针p先走,使p指向链表中的第m-n+1个结点;(m-n=长度差,又因为从0开始,所以-1)
若m<n,则使q指向链表中的第n-m+1个结点,即 (使指针p和q所指的结点到表尾的长度相等)。 - 反复将指针p和q同步向后移动,当p、q指向同一位置时停止,即为共同后缀的起始位置,算法结束。
- 算法:
typedef struct Node {
char data;
struct Node *next;
}SNode;
//求链表长度
int listlen(SNode *head) {
int len = 0;
while(head->next!=NULL) {
len++;
head = head->next;
}
return len;
}
//找出共同后缀的起始地址(所以不能改变链表),不然地址变了
SNode *find_addr(SNode *str1, SNode *str2) {
int m, n, i;
SNode *p, *q;
m = listlen(str1);
n = listlen(str2);
for(i = 0, p=str1; i<m-n+1; i++) { //找到第m-n+1个结点 //或者i = 1, p=str1; i<=m-n+1; i++
p = p->next;
}
for(i = 0, q=str2; i<n-m+1; i++) {
q = q->next;
}
while(p->next!=NULL && p->next!=q->next) {
p = p->next;
q = q->next;
}
return p->next;
}- 效率:
时间复杂度:O(len1+len2),其中len1、len2分别为两个链表的长度
空间复杂度:O(1)
归纳总结
- 对于链表,经常采用的方法有:头插法、尾插法、逆置法、归并法、双指针法等,对具体问题需要灵活变通;
- 对于顺序表,由于可以直接存取,经常结合排序和查找的几种算法设计思路进行设计,如 归并排序、二分查找等。