(挂惨了 我晚上一定好好睡觉。
T1 求冒泡排列在第几轮结束。(nleq 3e7)
可以发现每次自己左边最大的数字是向右移动的 所以答案为max{自己左边有多少个数比自己大}
想要O(n)求出的话还要再考虑一下 如何求出max 由于是max 我们考虑自己右边最多有多少比自己小的max等价于原答案。
所以我们可以发现 利用较小的数字来统计答案会比用较大的数字统计答案更优 换个说法 (a_i<a_j) (a_i)和(a_j)如果进行换位了 那么我们只统计(a_i)的对答案的
贡献至少不会比(a_j)要小。一个很难得到最很好好证明的答案:max{i-(a_i)}即为答案。
考虑证明:一个数字前面包括本身最多有(a_i)个数对答案没有贡献。考虑如果不够这(a_i)个数 那么一定有比自己还要小的数字在自己后面 那么这样统计下去至少能够找到答案。
bf:
const int MAXN=30000010;
int n;
ll S,B,C,D;
int a[MAXN],c[MAXN];
int cnt,ans;
int main()
{
freopen("bubble.in","r",stdin);
freopen("bubble.out","w",stdout);
get(n);get(S);get(B);get(C);get(D);
rep(1,n,i)
{
a[i]=i;
S=(S*B+C)%D;
swap(a[i],a[(S%i)+1]);
}
//rep(1,n,i)cout<<a[i]<<' '<<endl;
rep(1,n,i)
{
int w=a[i];cnt=0;
while(w)
{
cnt+=c[w];
w-=w&(-w);
}
ans=max(ans,i-1-cnt);
w=a[i];
while(w<=n)
{
++c[w];
w+=w&(-w);
}
}
put(ans);
return 0;
}
sol:
const int MAXN=30000010;
int n;
ll S,B,C,D;
int a[MAXN],c[MAXN];
int cnt,ans;
int main()
{
freopen("1.in","r",stdin);
get(n);get(S);get(B);get(C);get(D);
rep(1,n,i)
{
a[i]=i;
S=(S*B+C)%D;
swap(a[i],a[(S%i)+1]);
}
//rep(1,n,i)cout<<a[i]<<' '<<endl;
rep(1,n,i)ans=max(ans,i-a[i]);
put(ans);
return 0;
}
T2:

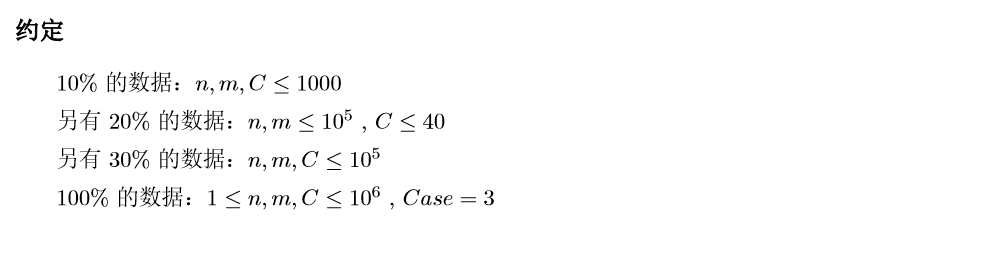
sb匹配题...无语。(每次我都暴力 每次暴力还挂。我真是个菜鸡。
容易推出性质 两个匹配的字符串a,b a种某种字符只能对应b上的位置只能对应一种字符 b种也同理 容易证明这样是可以匹配的充要条件。
可以简单证明一下:如果满足上述条件 那么直接swap即可 可以发现这样做就可以形成一模一样的字符。考虑必要条件的证明:反证:如果不满足上述情况 那么必然某种字符对应了两种字符 而swap每次只能将一种字符变成另外一种字符 如果swap是那两种字符 显然无法匹配还是原来的情况 如果不是 显然还是原情况。证毕。
所以现在问题变成了 给出两个字符串看 是否满足上述条件。考虑暴力 n^2 匹配。最尴尬的事实是优化不了 这个思路虽然没错 但是 必须一一得到位置信息。
贴一发暴力代码:
const int MAXN=1000010;
int T,C,n,m,top;
int ans[MAXN];
int a[MAXN],b[MAXN],c[MAXN],c1[MAXN],cnt,cnt1;
vector<int>w[MAXN];
int main()
{
freopen("1.in","r",stdin);
//freopen("match.out","w",stdout);
get(T);get(C);
while(T--)
{
get(n);get(m);top=0;
rep(1,C,i)w[i].clear();
rep(1,n,i)get(a[i]);
rep(1,m,i)get(b[i]),w[b[i]].pb(i);
rep(1,n-m+1,i)
{
int cnt=0;
rep(1,C,j)
{
if(w[j].size())
{
int last=0;
rep(0,w[j].size()-1,k)
{
int ww=w[j][k];
if(last&&last!=a[i+ww-1]){cnt=1;break;}
last=a[i+ww-1];
if(c[last]&&c[last]!=j){cnt=1;break;}
c[last]=j;
}
if(cnt)break;
}
}
rep(1,C,j)c[j]=0;
if(!cnt)ans[++top]=i;
}
put(top);
rep(1,top,i)printf("%d ",ans[i]);
puts("");
}
return 0;
}
可以发现这是一个sb匹配题 我们可以考虑算法了 hash 或者 KMP(关于自己的子串和模式串的匹配问题。
hash不太会 但是考虑KMP的话 我们可以通过性质定义一种匹配 自己上次的字符的匹配位置和当前位置的差 恰好等于自己匹配到的字符的上次位置和这次位置的差值。如果完全符合的话显然和我们的性质是刚好吻合的。
考虑KMP做这件事 接下来是魔改KMP...(这题的暴力分给的很不合理 推出性质之后暴力只有10分 正解KMP想出来了才能拿100.果然算法要套到题目上 这个角度来思考这道题更容易出解 而不是得到性质之后套到暴力之上。
建立数组 la[i] 表示 a串的i的上一个位置和当前位置的差值 lb[i]同理 进行匹配即可。
值得注意的是 存在断层现象 可能当前匹配的长度为 w w+1上一次出现的位置与w+1的差是大于w的 此时默认为w+1上的字符为第一次出现 那么值为w+1即可。
剩下的就没有了。复杂度O(n)
const int MAXN=1000010;
int T,C,n,m,top;
int ans[MAXN];
int a[MAXN],b[MAXN],c[MAXN],la[MAXN],lb[MAXN];
int nex[MAXN];
inline void KMP()
{
int j=0;top=0;
rep(2,m,i)
{
while(min(j+1,lb[i])!=lb[j+1]&&j)j=nex[j];
if(min(j+1,lb[i])==lb[j+1])++j;
nex[i]=j;
}
j=0;
rep(1,n,i)
{
while(min(j+1,la[i])!=lb[j+1])j=nex[j];
if(min(j+1,la[i])==lb[j+1])++j;
if(j==m)j=nex[j],ans[++top]=i;
}
}
int main()
{
freopen("1.in","r",stdin);
//freopen("match.out","w",stdout);
get(T);get(C);
while(T--)
{
get(n);get(m);
rep(1,C,i)c[i]=0;
rep(1,n,i)
{
get(a[i]);
la[i]=i-c[a[i]];
c[a[i]]=i;
}
rep(1,C,i)c[i]=0;
rep(1,m,i)
{
get(b[i]);
lb[i]=i-c[b[i]];
c[b[i]]=i;
}
KMP();
put(top);
rep(1,top,i)printf("%d ",ans[i]-m+1);
puts("");
}
return 0;
}
T3:

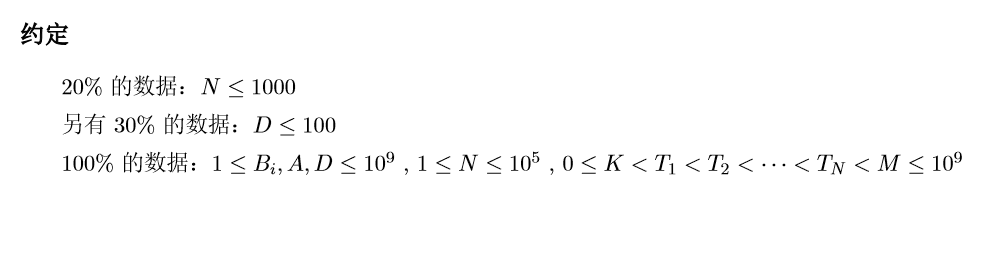
一道没见过的dp优化题目。
看出来dp之后可以列状态f[i]表示到达第i页的最大价值。
页数1e9当场gg 很容易发现和页数无关 之和我们到达第i个关键点了没有有关。
考虑最优策略 一定是从第K页一路上经过若干个关键点过来的。f[i]表示到达第i个点的最大价值。
容易得到转移 (f[i]=f[j]-lceilfrac{(T_i-T_j)}{D} ceilcdot A+B_i)
转移是(n^2)的 暂时看不出来怎么优化。
不过这个向上取整的式子我倒是可以拆成向下取整。
(lceilfrac{a}{b} ceil=frac{a-1}{b}+1)
没啥用。。。
不过这倒是可以进一步化简这个式子。
(lfloorfrac{a-c}{b} floor=frac{a}{b}-frac{c}{b})-(a%b<c%b)
到这里可以发现 还是没有任何用 我只不过在玩这个式子罢了/cy 至少对写暴力有很大的优化...
bf score:20
const ll MAXN=100010;
ll f[MAXN];
ll K,M,D,A,n,maxx=-INF;
ll a[MAXN],b[MAXN];
signed main()
{
freopen("1.in","r",stdin);
//freopen("reading.out","w",stdout);
f[0]=0;get(K);get(M);get(D);get(A);get(n);
rep(1,n,i)get(a[i]),get(b[i]),f[i]=-INF;a[0]=K;
//if(n<=1000)
{
rep(1,n,i)
{
rep(0,i-1,j)
{
ll w=(a[i]-a[j]-1)/D+1;
f[i]=max(f[i],f[j]+b[i]-w*A);
}
}
rep(0,n,i)
{
ll w=(M-a[i]-1)/D+1;
f[i]=f[i]-w*A;
maxx=max(maxx,f[i]);
}
putl(maxx);
}
return 0;
}
考虑题目中的子任务 D<=100
观察我们的dp式如果存在 j<k 且j和k 模D同余 我们从dp的角度分析从j转移过来没啥用 直接从k转移即可。
这样我们得到了一个非常好些的 nD的dp.
接下来就要让这两个方法结合 其实光我第一个dp就可以推出正解。
考虑dp式的化简 (f[i]=f[j]-lceilfrac{(T_i-T_j)}{D} ceilcdot A+B_i) 这个向上取整等价于 (frac{T_i}{D}-frac{T_j}{D})+((T_i)%D>(T_j)%D.
绝杀化简 对于任意一条路径来说 对于路径上两个相连的点 i j 他们对答案的贡献的(frac{T_i}{D}-frac{T_j}{D})的连续累加 恰好等于(frac{M}{D}-frac{K}{D}).
也就是说我们只需要管 后面那个东西 就行了 这其实是是否多了一个A的关系 采用数据结构优化一下即可。
区间查询最值 考虑线段树 (zkw线段树常数会很小很小。或者标记永久化 没必要懒标记了。这里推荐zkw.
考虑一下对于绝杀定理的证明 通过感性理解 严格观察 我可以发现是正确的 而并非证明/ll.
学了一发 zkw线段树 把这题A了 不是很想写普通线段树了...
const ll MAXN=100010;
ll f[MAXN];
ll K,M,D,A,n,maxx=-INF,top,num,base;
ll a[MAXN],b[MAXN],c[MAXN],val[MAXN<<2];
inline void discrete()
{
sort(c+1,c+1+num);
rep(1,num,i)if(i==1||c[i]!=c[i-1])c[++top]=c[i];
rep(0,n,i)a[i]=lower_bound(c+1,c+1+top,a[i])-c;
}
inline void build(ll len)
{
while(base<=len)base=base<<1;
rep(1,base*2,i)val[i]=-INF;
}
inline void modify(ll pos,ll x)
{
pos+=base;val[pos]=max(val[pos],x);pos=pos>>1;
while(pos)
{
val[pos]=max(val[pos<<1],val[pos<<1|1]);
pos=pos>>1;
}
}
inline ll ask(ll l,ll r)
{
ll res=-INF;
for(l=base+l-1,r=base+r+1;l^r^1;l=l>>1,r=r>>1)
{
if(~l&1)res=max(res,val[l^1]);//经过左儿子
if(r&1)res=max(res,val[r^1]);//经过右儿子
}
return res;
}
signed main()
{
freopen("1.in","r",stdin);
//freopen("reading.out","w",stdout);
get(K);get(M);get(D);get(A);get(n);
rep(1,n,i)get(a[i]),get(b[i]),a[i]%=D,c[i]=a[i];
num=++n;a[n]=M%D;c[n]=a[n];c[++num]=a[0]=K%D;discrete();
base=1;build(top);
modify(a[0],0);
rep(1,n,i)
{
ll w1=ask(1,a[i]-1)-A;
ll w2=ask(a[i],top);
f[i]=max(w1,w2)+b[i];
modify(a[i],f[i]);
}
putl(f[n]-(M/D-K/D)*A);
return 0;
}
脑子还是不够灵光 要努力猜结论 猜算法 将性质和算法联系在一起。