Support Vector machines
为什么人们称一种算法为机器,我也不知道(俄罗斯人发明)
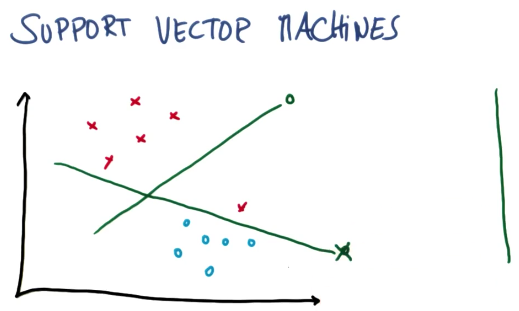
粗略的来说,支持向量机所做的就是去寻找分割线(separating)
或者通常称之为超平面,介于两个类别的数据之间
所以想象一下我们有一些两个不同类别的数据,SVM是一种算法,通过采用这些数据作为输入
然后输出一条线,来将这些数据分类。
好的分隔线有何特点

这条线它最大化了到最近点的距离,并且它对涉及的两个分类均最大化了此类距离
这是一条在每个分类里均最大化了到最近点的距离的线
而这个距离通常被称之为间隔(margin),这是一个被最大化了的东西
间隔 就是线与两个分类中最近点的距离

是因为这条线不容易出现分类误差,如果选择非常靠近现有数据的线,细微的噪声也会
使那边的标签倒转,从而感到没有那么稳定,所以支持向量机的内部原理是
SVM的原理是:最大限度地提升结果的稳定性(result)
SVM总是将正确的分类标签作为首要考虑,然后对间隔进行最大化
SVM 对异常值的响应
有时候对于SVM来说,可能无法正确 完成工作

对于不存在能将两个类分割的决策面,你可以将这个点看作是异常值
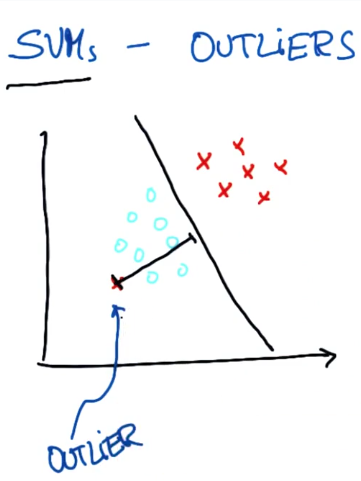
最好是像这样作为一个决策边界,直接把受影响的一点标在另一边
其实SVM足以做到这一点,它经常能找到使两个数据集间距最大化的决策边界
同时默许单个异常值(outliers),就像上图显示的
但应该知道的一点是SVM实际上对异常值的情况较为健壮,这在某种程度上
均衡了它找出最大距离的间隔和忽略异常值的能力
显然这也是有代价的,我们可以看到SVM参数决定了它如何检测新的异常值
SKlearn 中的 SVM
http://scikit-learn.org/stable/modules/svm.html
from sklearn import svm X = [[0, 0], [1, 1]] y = [0, 1] clf = svm.SVC() clf.fit(X, y) clf.predict([[2., 2.]])
import statement, training features, traning labels,create classifier
导入语句,训练特征,训练标签,创建分类器,并使用训练特征和训练标签进行拟合,以及如何进行预测
scikit-learn的优点之一:基本上我们要查看的所有分类器以及未来你可能自行使用的所有分类器
都遵循这一相同的模式where you import it, you create it, you fit it, you make predictions
即导入、创建、拟合 然后预测,而且语法也相同
SVM 决策边界
SVM Decision Bounddary
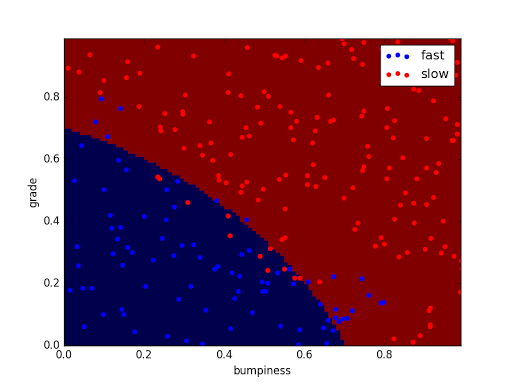
贝叶斯模型中,我们的决策边界可能有点点弯曲

现在我们的SVM决策边界是笔直的
当然,这条线会在决策边界与任何未分类点之间提供最大间隔,所以两边都有数据点

为了对这一特定示例进行更详细的说明,这表示它需要尽可能增大所有这些距离
也就是决策边界附近的点,它(SVM)要试图找到一个决策边界使所有这些短橙色线尽可能大
这意味着这两类数据有着尽可能大的间隔
import sys from class_vis import prettyPicture from prep_terrain_data import makeTerrainData import matplotlib.pyplot as plt import copy import numpy as np import pylab as pl features_train, labels_train, features_test, labels_test = makeTerrainData() #################################SVM################################## ### we handle the import statement and SVC creatin for you here from sklearn.svm import SVC clf = SVC(kernel = "linear") ### now your job is to fit the classifier ### using the training features/labels, and to ### make a set of predictions on the test data clf.fit(features_train, labels_train) ### store your predictions in a list named pred pred = clf.predict(features_test) from sklearn.metrics import accuracy_score acc = accuracy_score(pred, labels_test) def submitAccuracy(): return acc print acc
The first one is that I have to fit my classifier, and I have to fit it on the training table.
首先我必须拟合我的分类器,且我必须使它拟合训练数据
clf.fit(features_train, labels_train)
so that means passing features_train, and labels_train to my fit function
这意味着将features_train(训练特征)和labels_train(训练标签)传递到我的拟合函数(fit)
Then, the second thing is making a list of predictions.
然后第二件事是把预测结果放入一个列表中
So, I store to a list named pred, and that's just
所以我保存了一个名为pred的列表
pred = clf.predict(features_test)
the familiar predict function that we've seen with the Naive Bayes classifier.
它也使用了我们熟悉的朴素贝叶斯分类器所采用的预测函数
请记住,当我们在预测时,我们只需要传递一组信息,也就是特征,因为标签是我们希望预测的内容
而且当然,你们需要使用测试数据集而不是训练数据集
非线性 SVM

SVM是基于线性分割的分类器,那么它到底是如何绘制出这条让人惊讶的非线性决策边界的呢?

这两个类之间不存在好的线性超平面或者线性分割器,或者换句话说,很难在两个类之间画一条线
但是实际情况是:
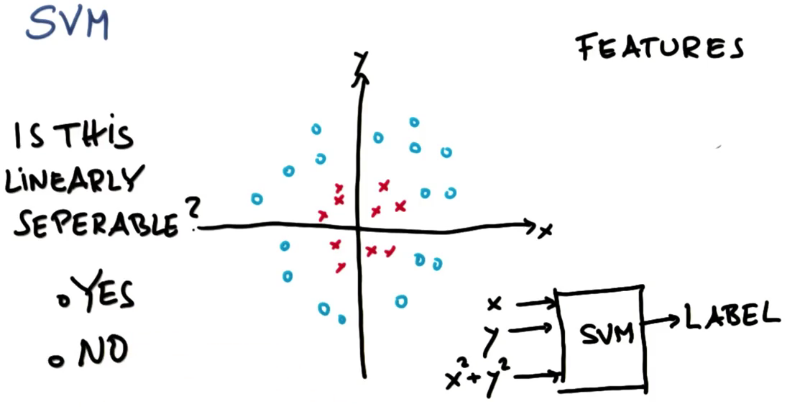
目前为止,我们认为我们把数据特征X和Y输入到这个神奇的SVM大盒子里,输出则是一个标签
(澄清一下,标签是在进行测试或预测时的输出。在训练时,
当然需要向算法提供标签,以帮助它计算出模式,这可能让标签听起来像是输入。
此处的要点在于,SVM中会进行特征转换,这会改变你对“线性可分”数据的看法。)
标签为蓝色圈或红色叉。我们要挑选一个对本例有帮助的特征,它就是x平方加上y平方
所以现在有一个三维的输入空间,可以在这三个特征上运行同样的算法,以前在两个特征上运行过
问题:
SVM现在还有效吗?或者换句话说这个新情况是否是线性可分的?
意思是说,如果这现在是我们的特征空间的话 ,我们能否找到一条直线或超平面来将这些叉和圈分开?
可视化新特征
如果我们的支持向量机学习了X的平方加Y的平方的类,让我们把这边的新特征称为z
那么我们知道z = x^2 + y^2 , 而且我们会尝试学习x、y和z之间的超平面
由于与起点之间存在距离z始终为 非负数
神奇的是,对于所有红点,离原点的距离都很小,对于所有蓝色圆圈,离原点的距离都很大
所以,让我们在这个新的xz的投影中显示完全相同的数据,舍弃y

我发现所有红点的z值都较小,而所有圆圈的z值都较大(z代表与原点的距离)
所以,如果将数据重新映射到带有z的新坐标系中,可以发现所有蓝色圆圈的z值都较大,所有红色的z值都较小
与新特征分隔

因此,由于我们添加了一个新的特征,并且我在这里选择了一个应该选择的新特征,由于我们增加了这个新特征
我们就能够使用支持向量机,以圆的形式学习非线性决策面



如果这个线性分割在x和y的原空间看,实际上就像上图,它是非线性的,因为它在这里有这个拐点
添加一个新的非线性特征|x|,即可使支持向量机把红点和蓝点线性分割开来
Kernel trick
核技巧,它们是获取低维度输入空间或特征空间,并将其映射到极高维度空间的函数
所以,过去不可线性分离的内容,变成可分离问题

这些函数被称为核函数,我们就不再深入任何细节,查看上图,这些不仅是具有特征空间的函数
而且是超过两维输入空间的函数 ,应用核函数技巧将输入空间从x和y,更改为更大的输入空间后,
再使用支持向量机分离数据点,然后获取解并返回原始空间,现在,你将得到一个非线性分割
这是支持向量机的一个重要的优点,你可以非常简单的找出最佳的线性分类器,或不同类之间的线性分割线
在更高的维度空间应用所谓的核函数技巧。实际上会获得一个极其强大的系统,在分割线为非线性时分离数据集
它是所有机器学习中最重要的技巧之一
核函数
通过sklearn的文档,了解在实际代码中是如何支持核的,观察是否有不同的核可以进行尝试,
观察其如何影响SVM给我们的决策边界
http://scikit-learn.org/stable/modules/svm.html
Versatile: different Kernel functions can be specified for the decision function.
Common kernels are provided, but it is also possible to specify custom kernels.
可以为不同的决策函数制定不同的核函数,有一些常见的核可以直接拿来即用,还有自定义核的选项
所以在能用的scikit-learn里,有几种不同的SVM ,我们正在使用的一个就是SVC
SVC(Support Vector Classifier)支持向量分类器
SVC支持向量分类器的另一个文档页
http://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html#sklearn.svm.SVC
class sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True,
probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1,
decision_function_shape=None, random_state=None)
上面是一个非常复杂的内容,告诉我可以创建自己的SVC,注意到那儿都是各种的命令参数,
在创建时都是可以传递的,其中一个就是核
kernel : string, optional (default=’rbf’) Specifies the kernel type to be used in the algorithm.
It must be one of ‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’ or a callable.
If none is given, ‘rbf’ will be used.
If a callable is given it is used to pre-compute the kernel matrix from data matrices;
that matrix should be an array of shape (n_samples, n_samples).
机器学习中的参数
Parameters in Machine Learning
(arguments passed when you create your classifier)参数是你在创建分类器时要传递的自变量
这发生在拟合之前,它们对你的算法所达到的决策边界产生巨大影响

现在要讨论的另外两个参数是C和gamma
C - controls the tradeoff between a smooth decision boundary and classifying training points correctly
它控制光滑决策边界,与正确分类所有训练点之间的折中
问题:
我们假设有一个很大的参数C,这是否意味着会获得一个光滑边界,或者会得到更多正确的训练点
这就是一个折中(tradeoff)
参数C值越大,就意味着你可以得到更多的训练点
实际上其含义就是C值越大,就可以得到更多复杂的决策边界,它可以弯曲绕过单独的数据点,
尽可能让所有东西都正确。但付出的代价是,可能比你想要的要复杂一些

弄明白你希望是一条直线的程度有多大
弄明白你希望是一条光滑决策边界相对于把分类弄对的程度有多大
这些当然是机器学习的艺术性的一部分
Over Fitting
过拟合
过度拟合是机器学习中的常见现象
每次做机器学习时候都要意识到这一点

你正确分类了红色数据,却在很多其他位置看起来非常奇怪,如果处理数据太过直接就会出现这样的情况
或者你的机器学习算法产生类似于此的复杂结果,而不是产生了像直线这样简单的结果,你就是过度拟合了
所以在机器学习中,我们其实是要避免过度拟合的
控制过度拟合的方法之一就是通过算法中的参数C、gamma还有kernel
这些不同类型的组合中,会让你或多或少的产生过度拟合
这就是机器学习的艺术性, 就是调节这些参数,所以你没有过度拟合你的数据
但是,我们将学习可以自动检测过度拟合的方法
SVM 的优缺点
支持向量机在具有复杂领域和明显的分隔边界的情况下,表现十分出色
但是在海量数据集中,它们表现的不太好,因为在这种规模的数据集中,训练时间将是立方数
另外在噪音过多的情况下,效果也不好 ,所以如果类严重重叠,你需要考虑独立证据,这时NB更好
所以问题又回到了, 你拥有的数据集和可用特征上,如果你有一个海量数据集,有很多很多的特征
直接可运行的SVM的速度可能会很慢,数据的某些噪音,可能会导致过拟合现象
应该在测试集上进行测试看看它的表现如何。