POJ 2074 Line of Sight(直线交点、最长连续区间）

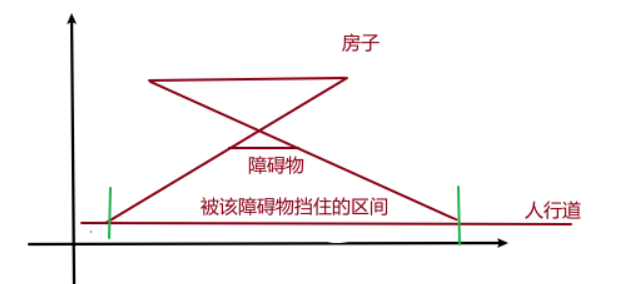
大意：

给出一个房子的两个端点坐标，以及观察线的左右端点坐标，n个障碍物，问观察线上能看到完整的房子的最长连续区间。

思路：

图源：https://blog.csdn.net/weixin_43311695/article/details/109193862

算出每个障碍物导致的视野盲区，然后计算不在盲区的最长区间即可。这里处理最长区间的方法是：将所有的盲区按照左端点排序，然后更新右边区间和答案即可。还需要注意的是，如果障碍物不在房子和观察线之间，那么不需要考虑。

注意一个小trick：下标从1开始记录盲区，因为这样可以避免讨论没有盲区的情况

#include <math.h>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <cstdio>
#include <iostream>
#include <map>
#include <queue>
#include <set>
#include <vector>

using namespace std;

const int N = 1e6 + 5;
typedef long long LL;
double dis[100][100];
// 计算几何模板
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
    if (fabs(x) < eps) return 0;  // =0
    if (x < 0)
        return -1;  // < 0
    else
        return 1;  // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }

struct Point {
    double x, y;
    int index;
    Point() {}
    Point(double _x, double _y) {
        x = _x;
        y = _y;
    }
    void input() { scanf("%lf%lf", &x, &y); }
    void output() { printf("%.2f %.2f
", x, y); }
    bool operator==(Point b) const {
        return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
    }
    bool operator<(Point b) const {
        return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
    }
    Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
    Point operator+(const Point &b) const { return Point(x + b.x, y + b.y); }
    //叉积
    double operator^(const Point &b) const { return x * b.y - y * b.x; }
    //点积
    double operator*(const Point &b) const { return x * b.x + y * b.y; }
    //返回两点的距离
    double dist(Point p) {
        return sqrt((x - p.x) * (x - p.x) + (y - p.y) * (y - p.y));
    }

    // 极角排序
};

struct Line {
    Point s, e;
    Line() {}
    // 两点确定一条线段
    Line(Point _s, Point _e) {
        s = _s;
        e = _e;
    }
    //返回点和直线(方向向量)关系
    // 1  在左侧; 2  在右侧; 3  在直线上
    int relation(Point p) {
        int c = sgn((p - s) ^ (e - s));
        if (c < 0)
            return 1;
        else if (c > 0)
            return 2;
        else
            return 3;
    }
    //两线段相交判断:规范相交：交点不在端点
    // 2 规范相交；1 非规范相交；0 不相交
    int segcrossseg(Line v) {
        int d1 = sgn((e - s) ^ (v.s - s));
        int d2 = sgn((e - s) ^ (v.e - s));
        int d3 = sgn((v.e - v.s) ^ (s - v.s));
        int d4 = sgn((v.e - v.s) ^ (e - v.s));
        if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2) return 2;
        return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
               (d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
               (d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
               (d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
    }
    bool parallel(Line v) { return sgn((e - s) ^ (v.e - v.s)) == 0; }
    //求两直线的交点
    //要保证两直线不平行或重合
    Point crosspoint(Line v) {
        double a1 = (v.e - v.s) ^ (s - v.s);
        double a2 = (v.e - v.s) ^ (e - v.s);
        return Point((s.x * a2 - e.x * a1) / (a2 - a1),
                     (s.y * a2 - e.y * a1) / (a2 - a1));
    }
    double length() { return s.dist(e); }
    //点到直线的距离
    double dispointtoline(Point p) {
        return fabs((p - s) ^ (e - s)) / length();
    }
    //点到线段的距离
    double dispointtoseg(Point p) {
        if (sgn((p - s) * (e - s)) < 0 || sgn((p - e) * (s - e)) < 0)
            return min(p.dist(s), p.dist(e));
        return dispointtoline(p);
    }
    //直线和线段相交判断
    //-*this line   -v seg
    // 2 规范相交
    // 1 非规范相交
    // 0 不相交
    int linecrossseg(Line v) {
        int d1 = sgn((e - s) ^ (v.s - s));
        int d2 = sgn((e - s) ^ (v.e - s));
        if ((d1 ^ d2) == -2) return 2;
        return (d1 == 0 || d2 == 0);
    }
};
struct Seq {
    double left, right;
    Seq() {}
    Seq(double _left, double _right) {
        left = _left;
        right = _right;
    }
};
Seq seq[N];
bool cmp(Seq a, Seq b) { return a.left < b.left; }
double x1, x2, y, px1, px2, py;
Line property, ob[N];
int n, cnt;
int main() {
    while (scanf("%lf%lf%lf", &x1, &x2, &y) != EOF && (x1 + x2 + y != 0)) {
        scanf("%lf%lf%lf", &px1, &px2, &py);
        property = Line(Point(px1, py), Point(px2, py));
        scanf("%d", &n);
        cnt = 0;
        seq[0] = Seq(0.0, 0.0);
        for (int i = 1; i <= n; i++) {
            double ox1, ox2, oy;
            scanf("%lf%lf%lf", &ox1, &ox2, &oy);
            if (oy >= y || oy <= py) continue;
            Line now = Line(Point(x2, y), Point(ox1, oy));
            Point lx = now.crosspoint(property);
            if (lx.x >= px2) continue;
            if (lx.x < px1) lx.x = px1;
            now = Line(Point(x1, y), Point(ox2, oy));
            Point rx = now.crosspoint(property);
            if (rx.x <= px1) continue;
            if (rx.x > px2) rx.x = px2;
            seq[++cnt] = Seq(lx.x, rx.x);
        }
        sort(seq + 1, seq + cnt + 1, cmp);
        double res = 0, r = px1;
        for (int i = 1; i <= cnt; i++) {
            res = max(res, seq[i].left - r);
            r = max(r, seq[i].right);
        }
        res = max(res, px2 - r);
        if (sgn(res) == 0)
            printf("No View
");
        else
            printf("%.2f
", res);
    }
}