设s数组为C的前缀和
首先$ans_i=min_{j<i}{ans_j+(i-j-1+s_i-s_j-L)^2}$
(斜率优化dp)参考(复读)https://www.cnblogs.com/orzzz/p/7885971.html
设j不比k劣,则$ans_j+(i-j-1+s_i-s_j-L)^2 <= ans_k+(i-k-1+s_i-s_k-L)^2$
化简,与i相关的放到一边,(由于要除法,设$k+s_k-j-s_j>0$)
得$2(i+s_i)<=frac{x_k-x_j+(k+s_k)^2-(j+s_j)^2+2(k+s_k)(L+1)-2(j+s_j)(L+1)}{k+s_k-j-s_j}$
设$f(k)=x_k+(k+s_k)^2+2(k+s_k)(L+1)$,$g(k)=k+s_k$,则$2(i+s_i)<=frac{f(k)-f(j)}{g(k)-g(j)}$
也就是说,当$g(k)>g(j)$时,当且仅当满足这个条件时,j不比k劣
对于每个j,都表示为二维平面上一个点$(g(j),f(j))$
如果有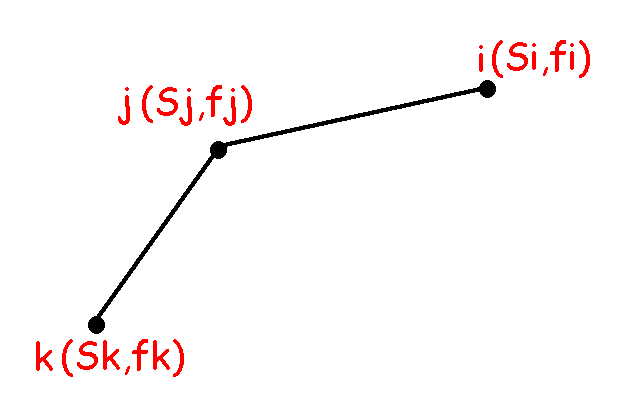 这样三个点i,j,k(图中横坐标分别改成g(i),g(j),g(k)),
这样三个点i,j,k(图中横坐标分别改成g(i),g(j),g(k)),
那么$frac{f(i)-f(j)}{g(i)-g(j)}<frac{f(j)-f(k)}{g(j)-g(k)}$
可以发现,不管$2(i+s_i)$会插入到与这两者有关的什么位置(比两者都小,夹在中间,比两者都大),j都不可能是最优解
因此,只有下凸壳上面的点才可能是最优解,可以在算出i的答案并加入i的同时维护一下下凸壳(此处$g(i)=i+s_i$是单调的,直接栈维护即可)
怎么样在下凸壳找到这个最优解呢?
考虑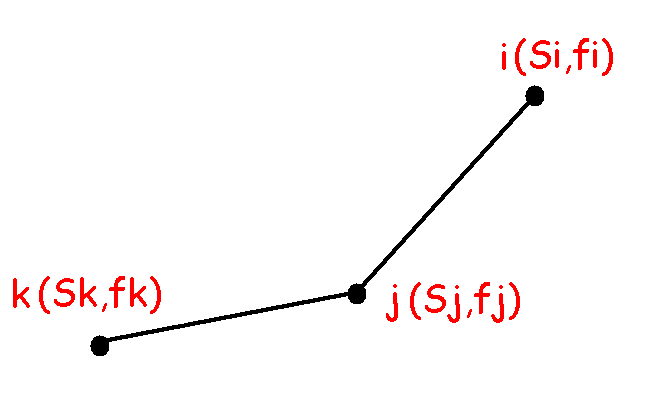 这样三个点i,j,k(图中横坐标分别改成g(i),g(j),g(k)),
这样三个点i,j,k(图中横坐标分别改成g(i),g(j),g(k)),
那么$frac{f(i)-f(j)}{g(i)-g(j)}>frac{f(j)-f(k)}{g(j)-g(k)}$
可以发现,如果$2(i+s_i)$比两者都大,那么i最优;如果夹在中间,则j最优;如果比两者都小,则k最优
把3个点扩展到很多个点,可以发现如果搞出一个线段集合,表示下凸壳相邻两点间连线的集合,在这个集合中取出一条斜率>$2(i+s_i)$并且最小的线段,这条线段靠前(靠左)的那个点就是最优解(意会一下)(下凸壳边界点可能要特判)
由于此处$2(i+s_i)$是单调的,可以用一个指针直接维护这个最优解的位置

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<vector> 5 using namespace std; 6 #define fi first 7 #define se second 8 #define mp make_pair 9 #define pb push_back 10 typedef long long ll; 11 typedef unsigned long long ull; 12 struct P 13 { 14 ll x,y,n; 15 }; 16 P operator-(const P &a,const P &b) 17 { 18 return (P){a.x-b.x,a.y-b.y,0}; 19 } 20 ll cross(const P &a,const P &b) 21 { 22 return a.x*b.y-b.x*a.y; 23 } 24 inline ll sqr(ll x){return x*x;} 25 P tmp[100011];int l,r; 26 int n;ll L; 27 ll s[100011],ans[100011]; 28 int main() 29 { 30 int i;ll t1;P tn; 31 scanf("%d%lld",&n,&L); 32 for(i=1;i<=n;++i) 33 { 34 scanf("%lld",s+i); 35 s[i]+=s[i-1]; 36 } 37 l=1;r=0; 38 tmp[++r]=(P){0,0,0}; 39 for(i=1;i<=n;++i) 40 { 41 t1=2*(i+s[i]); 42 while(l<r && tmp[l+1].y-tmp[l].y <= t1*(tmp[l+1].x-tmp[l].x)) ++l; 43 if(l>r) l=r; 44 ans[i]=ans[tmp[l].n]+sqr(i-tmp[l].n-1+s[i]-s[tmp[l].n]-L); 45 tn=(P){i+s[i],ans[i]+(i+s[i])*(i+s[i]+2*L+2),i}; 46 while(r>=2 && cross(tn-tmp[r-1],tmp[r]-tmp[r-1])>=0) --r; 47 tmp[++r]=tn; 48 } 49 printf("%lld ",ans[n]); 50 return 0; 51 }
为什么是凸包呢?好像还有一种解释方法
化简一下$ans_j+(i-j-1+s_i-s_j-L)^2$=$(i+s_i)^2-2(i+s_i)(j+s_j+L+1)+(j+s_j+L+1)^2+x_j$
其中$(i+s_i)^2$只与i有关,先提出去,
剩下$-2(i+s_i)(j+s_j+L+1)+(j+s_j+L+1)^2+x_j$
设其为z,现在要求z的最小值
发现这个过程类似线性规划,等式为$z=-2(i+s_i)(j+s_j+L+1)+(j+s_j+L+1)^2+x_j$
即$(j+s_j+L+1)^2+x_j=2(i+s_i)(j+s_j+L+1)+z$
设$x=j+s_j+L+1$,$y=(j+s_j+L+1)^2+x_j$,$a=2(i+s_i)$,则$y=ax+z$
对于每个j<i,可以看做平面上一个点(x,y),得到点集S
现在有直线$y=ax+z$,a是定值,z不确定,要使得它经过S中一个点,且截距z最小,就拿这条直线从右往左移,碰到第一个点时停下来
显然,只有点集的下凸壳上的点有可能被靠到(也有可能靠到下凸壳的一条边上,这时边的两个端点都是最优解)
下凸壳的性质是:形成它的各条线段的斜率递增
因此,要找到这条直线会靠到什么地方,维护下凸壳,在上面按斜率二分一下就行(这题有特殊性质,也可以用一个指针维护)
话说推出来的式子跟上面不一样,但是仍然可以A?

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<vector> 5 using namespace std; 6 #define fi first 7 #define se second 8 #define mp make_pair 9 #define pb push_back 10 typedef long long ll; 11 typedef unsigned long long ull; 12 struct P 13 { 14 ll x,y,n; 15 }; 16 P operator-(const P &a,const P &b) 17 { 18 return (P){a.x-b.x,a.y-b.y,0}; 19 } 20 ll cross(const P &a,const P &b) 21 { 22 return a.x*b.y-b.x*a.y; 23 } 24 inline ll sqr(ll x){return x*x;} 25 P tmp[100011];int l,r; 26 int n;ll L; 27 ll s[100011],ans[100011]; 28 int main() 29 { 30 int i;ll t1;P tn; 31 scanf("%d%lld",&n,&L); 32 for(i=1;i<=n;++i) 33 { 34 scanf("%lld",s+i); 35 s[i]+=s[i-1]; 36 } 37 l=1;r=0; 38 tmp[++r]=(P){L+1,sqr(L+1),0}; 39 for(i=1;i<=n;++i) 40 { 41 t1=2*(i+s[i]); 42 while(l<r && tmp[l+1].y-tmp[l].y <= t1*(tmp[l+1].x-tmp[l].x)) ++l; 43 if(l>r) l=r; 44 ans[i]=ans[tmp[l].n]+sqr(i-tmp[l].n-1+s[i]-s[tmp[l].n]-L); 45 tn=(P){i+s[i]+L+1,ans[i]+sqr(i+s[i]+L+1),i}; 46 while(r>=2 && cross(tn-tmp[r-1],tmp[r]-tmp[r-1])>=0) --r; 47 tmp[++r]=tn; 48 } 49 printf("%lld ",ans[n]); 50 return 0; 51 }
其他资料(未看,咕咕咕)
https://www.cnblogs.com/MashiroSky/p/6009685.html
https://blog.csdn.net/lxc779760807/article/details/51366552
https://codeforces.com/blog/entry/63823
https://www.cnblogs.com/flashhu/p/9480669.html
待修正:不妨设... 直线y=ax+z(a>0??)
