你将获得 K 个鸡蛋,并可以使用一栋从 1 到 N 共有 N 层楼的建筑。
每个蛋的功能都是一样的,如果一个蛋碎了,你就不能再把它掉下去。
你知道存在楼层 F ,满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎,从 F 楼层或比它低的楼层落下的鸡蛋都不会破。
每次移动,你可以取一个鸡蛋(如果你有完整的鸡蛋)并把它从任一楼层 X 扔下(满足 1 <= X <= N)。
你的目标是 确切地 知道 F 的值是多少。
无论 F 的初始值如何,你确定 F 的值的最小移动次数是多少?
示例1:
输入:K = 1, N = 2
输出:2
解释:
鸡蛋从 1 楼掉落。如果它碎了,我们肯定知道 F = 0 。
否则,鸡蛋从 2 楼掉落。如果它碎了,我们肯定知道 F = 1 。
如果它没碎,那么我们肯定知道 F = 2 。
因此,在最坏的情况下我们需要移动 2 次以确定 F 是多少。
示例2:
输入:K = 2, N = 6
输出:3
示例1:
输入:K = 3, N = 14
输出:4
提示:
1 <= K <= 1001 <= N <= 10000
动态规划
什么是动态规划
动态规划英文 Dynamic Programming, 是求解决策过程最优化的数学方法,后来沿用到了编程领域。
动态规划的大致思路是把一个复杂的问题转化成一个分阶段逐步递推的过程,从简单的初始状态一步一步递推,最终得到复杂问题的最优解。
动态规划的过程
- 寻找状态转移方程式
- 利用状态方程是自底向上求解问题
于是我们可以用动态规划的方法来解决此鸡蛋问题。动态规划的关键就在于寻找到状态转移方程式。在此问题中,我们可以把m层楼和n个鸡蛋的问题转化成一个函数F(m,n),其中楼层m和鸡蛋n是函数的两个参数,而函数的值则是最优解的最大尝试次数。
假设我们第一个鸡蛋认出的位置在第x层(1<=x<=m),会出现两种情况:
- 鸡蛋没碎
那么剩余m-x层数,剩余n个鸡蛋,可以转化为以下的函数:
F(m-x, n) + 1, 1 <= x <= m
- 鸡蛋碎了
那么剩余x-1层数,剩余n-1个鸡蛋,可以转化为以下的函数:
F(x-1, n-1) + 1, 1 <= x <= m
根据这两个状态转移式,我们可以得知要在最差状态下的到最优解,首先最差的状态就是
max{F(m-x, n) + 1,F(x-1, n-1) + 1}
最优解就是
min{max{F(m-x, n) + 1,F(x-1, n-1) + 1}, 1 <= x <= m}
算出此状态转移式后,我们还需要知道一个边界状态,通过分析我们可以发现,1. 只有一层楼时无论多少鸡蛋都只需要一次即可得出结论。2.只有一个鸡蛋时,有多少层就需要试多少层。所以有以下的式子:
F(1, n) = 1;
F(m, 1) = m;
有了这些完整的状态转移方程式,我们就可以从底层开始逐渐向上求解,下面就用表格展示一下F(4,3):
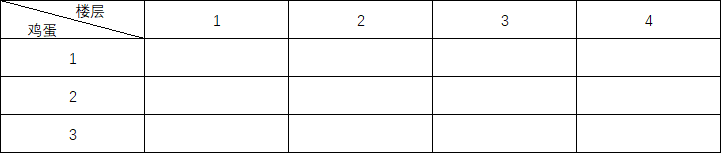
首先根据边界条件,可以填入出第一行和第一列的值:
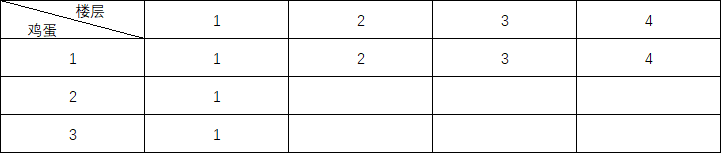
接下来就要计算F(2,2)了,套用上面的状态转移方程式:
F(2,2) = min{max{F(2-x, 2) + 1,F(x-1, 1) + 1}, 1 <= x <= 2}
计算后可以得出F(2,2) = 2,于是将2填入表格中:
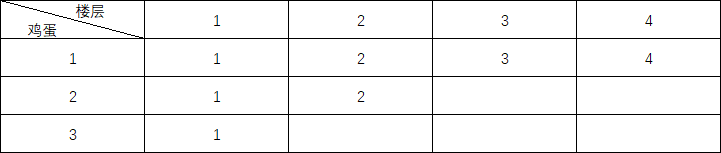
然后依次计算得出后面的值,最终可以得到F(4,3)的结果,如下表:
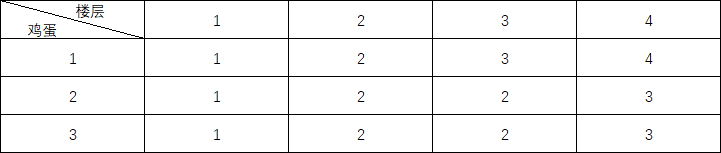
最终得出F(4,3)=3,代码的实现如下
int superEggDrop(int eggs, int floors) {
int i, j, k, t, max;
int temp[eggs + 1][floors + 1];
for(i = 0; i < floors + 1; ++i)
{
temp[0][i] = 0;
temp[1][i] = i;
}
for(i = 2; i < eggs + 1; ++i)
{
temp[i][0] = 0;
temp[i][1] = 1;
}
for(i = 2; i < eggs + 1; ++i)
{
for(j = 2; j < floors + 1; ++j)
{
for(k = 1, max = UINT_MAX; k < j; ++k)
{
t = temp[i][j - k] > temp[i - 1][k -1] ? temp[i][j - k] : temp[i - 1][k -1];
if(max > t)
{
max = t;
}
}
temp[i][j] = max + 1;
}
}
return temp[eggs][floors];
}
该算法的空间复杂度是O(nm),时间复杂度是O(nm^2),很显然这个时间复杂度过高,无法满足题目要求,所以现在需要进一步优化此算法。
首先这个算法是我们根据状态转移方程式实现的,所以要想在时间上进行优化,有很大的苦难。于是我们就需要转换我们的思维,我们先递推出30层楼,4个鸡蛋的表格:

通过分析表格,我们可以发现F(26,2)=7,F(27,2)=7,F(28,2)=7,此时若再加一层F(29,2)=8。2个鸡蛋,在22-28层时测试7次就可以解决问题,可是当到了第29层时就会需要多测试一次。于是我们可以引出一下的问题:
n个鸡蛋,测试m次(简记为D(n,m)),最大可以解决几层楼的问题
通过对递推结果表格的观察,我们可以得到如下结论:
- D(1,m) = m;
- D(n,n) = 2^n - 1;
- D(1,m){m <= n} = D(m,m);
对于第二点,以D(4,4)为例,我们第1次在8楼扔下鸡蛋,如果碎了,则第二次在4楼扔下鸡蛋,否则在12楼扔下鸡蛋,对于在4楼扔下鸡蛋的情况,之后可以分别在2楼或者6楼扔下鸡蛋,如此进行,就可以找到答案楼层,方法与二分查找一样。例如答案楼层是5的情况,测试序列为8,4,6,5。
对于第三点,如果有5个鸡蛋让你测试3次,即使三次测试鸡蛋都碎了,剩下的2个鸡蛋也派不上用场,所以D(5,3) = D(3,3)
发现这些关系之后,我们似乎找到解决n个鸡蛋测试m次最大能够解决楼层数的方法。对于D(n,m){n < m}而言,对于其能够测试的最大楼层数k,我们可以构造这样的场景,将第一颗鸡蛋仍在楼层i,使得第i + 1层到第k层是D(n,m-1)可以解决的最大楼层数,第1层到第i - 1层是D(n-1,m-1)可以解决的最大楼层数,由此得到递推关系D(n,m) = D(n -1,m-1) + 1 + D(n,m-1),然后对D(n,m-1),D(n-1,m-1)再按照上述公式分解,直到得出刚才所列的三种可计算情况(n = 1,或者m <= n)为止,再进行回溯累加,就可以得到D(n,m)的值,代码如下:
int DroppingMax(int eggs, int times)
{
if(eggs == 1)
{
return times;
}
if(eggs >= times)
{
return (int)pow(2, times) - 1;
}
return DroppingMax(eggs, times -1) + DroppingMax(eggs -1, times - 1) + 1;
}
根据此算法,我们可以得出D(2,5)=15,D(2,8)=36,也就是说,2个鸡蛋测试5次最多可以解决15层楼的问题,测试8次最多可以解决36层楼的问题。可见,出这个题的人并不是随便找两个楼层数陪咱们玩玩,而是对此问题认真研读后的结果。有了此利器之后,我们解决扔鸡蛋问题的的方法将得到大幅简化,对于n个鸡蛋解决k层楼的问题我们只需找到这样的值m,使得D(n,m-1)< k <=D(n,m),代码如下
int superEggDrop(int eggs, int floors)
{
int times = 1;
while(DroppingMax(eggs, times) < floors)
{
++times;
}
return times;
}
该算法的时间和空间复杂度不太好分析,但都要好于传统的DP算法,有兴趣的读者可以推敲一下。