数学篇之高斯消元

众所周知，高斯消消乐很好玩（并不），并且理解很简单，代码也很“简单”（蒟蒻到听了n遍还是不会写代码，在此写篇博客记下来）

高斯消元：

高斯消元是用来解线性方程组的，即把一个方程组的系数与方程右边的数写成一个矩阵，再解这个矩阵对应的行列式的值，就可以快速的求解

一个行列式有如下几种初等变换：

1.交换两行（列），行列式的值变号。

2.某行（列）的所有数，同时乘上k，行列式的值相当于原来的k倍（但某行（列）加上某个数的k倍值是不变的）

3.某行（列）的所有数同时加上a,行列式的值不变

so高斯消元应该怎么消呢？

（高斯消元以列为单位消）

step1：先将第一行第一列的数化为1，并且同一行的数做相同变换

step2：再将其余行的第一列化为0（通过加/减1的k倍），并且同一行的数做相同变换

step3：这时，第一行就处理完了，再将原本的第二行视作新的第一行，且新的第一列为原本的第二列（就是把原来矩阵的第一行第一列扔掉），做相同的变换，一直处理到原本的第n-1行，这样矩阵就消完了。接下来就是回带求解

当然，如果有一行全是0的时候会出现无解或有无穷多解，要特判。

因为这是解方程用的，所以输入的矩阵每一行格式如下：

 系数1   系数2....................系数n    等号右边的数（这点很重要）

总体格式如下：

|a11................a1n    b1|

|a21...............a2n     b2|

|...................................|

|an1...............ann     bn|

其中a都是系数，b为等号右边的数

高斯消元的目的是把所有的a组成的矩阵消成单位矩阵，这样最后消出来的方程就是

a11*x=b1

a22*y=b2

.....

ann*k=bn

所有的a和b都是消完后的数

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int n,mo=100000007;
double a[1001][1001];
int main()
{    bool sc=0;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)//读入没什么好说的
      for(int j=1;j<=n+1;j++)
         scanf("%lf",&a[i][j]);
     int bj,flag=0;
     for(int i=1;i<=n;i++)
       {bj=i;
          while(a[bj][i]==0&&bj<=n)
          bj+=1;
          if(bj==n+1){ flag=1;continue;//如果有一列全0，那么它就没有价值了
          }
          for(int j=1;j<=n+1;j++)swap(a[i][j],a[bj][j]);//交换，使第一行第一列的数不为0
          double kk=a[i][i];//确保对角线上的数是1
          for(int j=1;j<=n+1;j++)
           {a[i][j]/=kk;//其余数跟着处理
           }
      //接下来这一坨可能会比较难理解，在下面再讲一下
          for(int j=1;j<=n;j++)//这一坨就是把经过处理对角线后的矩阵消成纯正的单位矩阵（就是除了对角线以外的数都清0）
          {if(i!=j){double k=a[j][i];//k=这行第一个数
               for(int m=1;m<=n+1;m++)
               {a[j][m]-=k*a[i][m];//此行所有的数减去第一个数*k，使第一个数变0，当后面再处理时因为上个数已经是0了，所以没有影响
               }
             }
           }
          if(i==n)//消完输出
          {for(int j=1;j<=n;j++)
           {for(int m=1;m<=n+1;m++)
             cout<<a[j][m]<<" ";
             cout<<endl;
             sc=1;
           }
          }
       }
       if(!sc)printf("False");//sc就是输出啦，如果无输出，就代表无解
}

补锅：

上面一坨东西只保证了对角线是1，但其他数还是一撮魑魅魍魉，我们要把这些魑魅魍魉都消成0.

可能用图来表示要好一些  

这货是对角线被处理过的玩意-------------->j从1开始，到n，模拟1到n行，同时，列用k代替。

            

    k每跑完1次，j就+1，即进行下一行。但i是不变的，这样就是以i为“主体”，对i后面的每一行进行操作，使其变为一个更小的方阵。（因为每跑完一遍这一坨，第i列以前就被消成0，除了对角线，那它就消好了，后面就不用管了）这样对角线确实会变，但下一轮循环i的时候对角线会被维护，且之前消成0的数不会被改变

其思路类似下图

 第一遍                                                                          第二遍（消阴影部分）

 

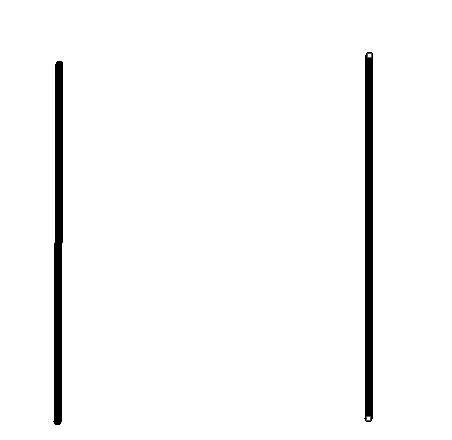
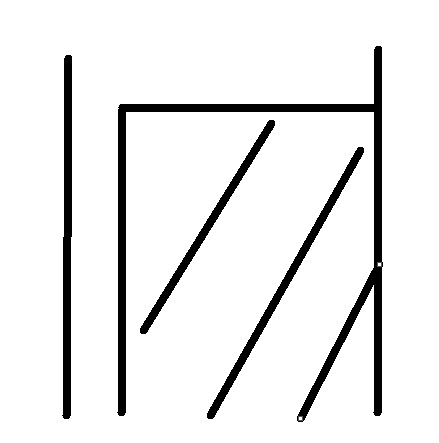
                第三遍

 

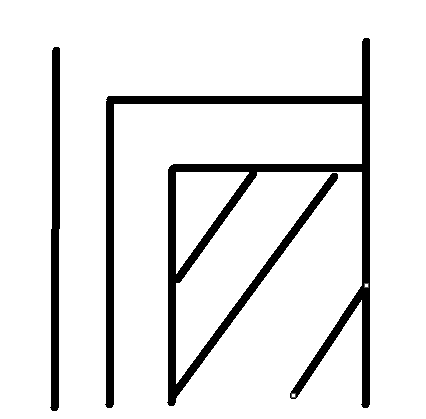
其实就是把大矩阵消成小矩阵，一直到消完（白色部分是一定不会变化的数，也就是消好的对角线和0）

 补锅*2：

    很多人问flag是干嘛用的，那是用来判断是无解还是有无穷多解的东西，不过一时懒脑细胞耗尽没有写上

    如何判断是有无穷解还是无解呢？

    既然我们有了flag=1（系数有一行全是0）,那么这个方程组不是无解就是无穷多解

   什么情况下会无解？

    那就是有一行系数全是0，但是方程结果不是0，就会无解。

    这样我们就可以把消完的矩阵全判一遍，如果都不是无解，就是有无穷多解了

   完整版代码如下：

   

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int n,mo=100000007;
double a[1001][1001];
long double wucha=1e-9;
bool pd(int h)
{ if(a[h][n+1]<wucha)return 1;//这里double类型的数会有一个误差，若这个数等于0，就是小于这个误差
     for(int i=1;i<=n;i++)
       {if(a[h][i]>wucha)return 1;
        }
        return 0; 
}
int main()
{    
    scanf("%d",&n);
    for(int i=1;i<=n;i++)//读入没什么好说的
      for(int j=1;j<=n+1;j++)
         scanf("%lf",&a[i][j]);
     int bj,flag=0;
     for(int i=1;i<=n;i++)
       {bj=i;
          while(a[bj][i]==0&&bj<=n)
          bj+=1;
          if(bj==n+1){ flag=1;continue;//如果有一列全0，那么它就没有价值了
          }
          for(int j=1;j<=n+1;j++)swap(a[i][j],a[bj][j]);//交换，使第一行第一列的数不为0
          double kk=a[i][i];//确保对角线上的数是1
          for(int j=1;j<=n+1;j++)
           {a[i][j]/=kk;//其余数跟着处理
           }
          for(int j=1;j<=n;j++)//这一坨就是把经过处理对角线后的矩阵消成纯正的单位矩阵（就是除了对角线以外的数都清0）
          {if(i!=j){double k=a[j][i];//k=这行第一个数
               for(int m=1;m<=n+1;m++)
               {a[j][m]-=k*a[i][m];//此行所有的数减去第一个数*k，使第一个数变0，当后面再处理时因为上个数已经是0了，所以没有影响
               }
             }
           }
          if(i==n)//消完输出
          {for(int j=1;j<=n;j++)
           {for(int m=1;m<=n+1;m++)
             cout<<a[j][m]<<" ";
             cout<<endl;
             
           }
          }
       }
      if(flag)
       {for(int i=1;i<=n;i++)
          if(!pd(i)){printf("No Solution!");return 0;
          }
          printf("Many Many Solutions!");//瞎写的不要在意那么多细节（比如语法什么的） 
       } 
}

吐血三升后肝出来的高消

高斯消消乐真好玩QwQ

诸位大佬们有觉得注释不详细的地方说出来好不好