1、图的的定义
前言
前面我们学习了线性表,栈、队列和树。前面三者都属于线性表范畴,它的的数据元素是被串起来的,仅有线性关系,每个元素仅有一个直接前驱和一个直接后继,是属于一对一关系。在树里面,每个元素之间存在着明显的层次关系,每一层的元素可能和下一层的多个元素相关,但只能和上一层的一个元素相关,属于一对多的关系。而图是一种较线性表和树更为复杂的数据结构,在图的结构中,节点和节点的关系是任意的,图中任意两个数据元素都可能相关。

定义:图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
在图中需要注意的是:
(1)线性表中我们把数据元素叫元素,树中将数据元素叫结点,在图中数据元素,我们则称之为顶点(Vertex)。
(2)线性表可以没有元素,称为空表;树中可以没有节点,称为空树;但是,在图中不允许没有顶点(有穷非空性)。
(3)线性表中的各元素是线性关系,树中的各元素是层次关系,而图中各顶点的关系是用边来表示(边集可以为空)。
2、图的分类
(1)按照有无方向,可将图分为有向图,无向图。
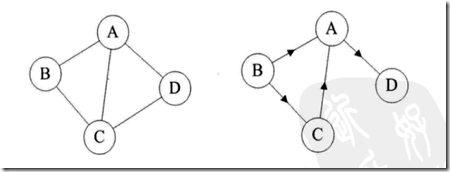
连接A到D的有向边称为弧,A是弧头,D是弧尾,用<A,D>表示,方向不能反。
表示方法:对于右图,G2来说,G2=(V2,{E2}) 其中顶点集合V2={A,B,C,D};弧集合 E2={<A,D>,<C,A>,<B,C>,<B,A>}
无向边用()表示,有向边用<>表示
(2)①无向完全图:在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。(含有n个顶点的无向完全图有(n×(n-1))/2条边)如下图所示:
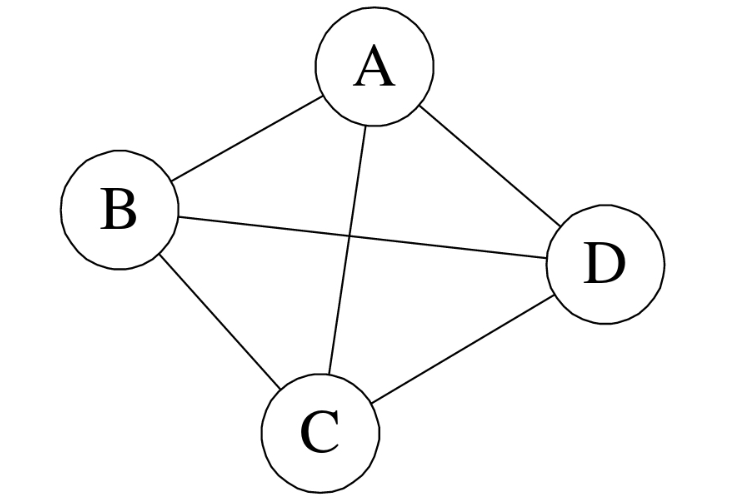
②有向完全图:在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。(含有n个顶点的有向完全图有n×(n-1)条边)如下图所示:
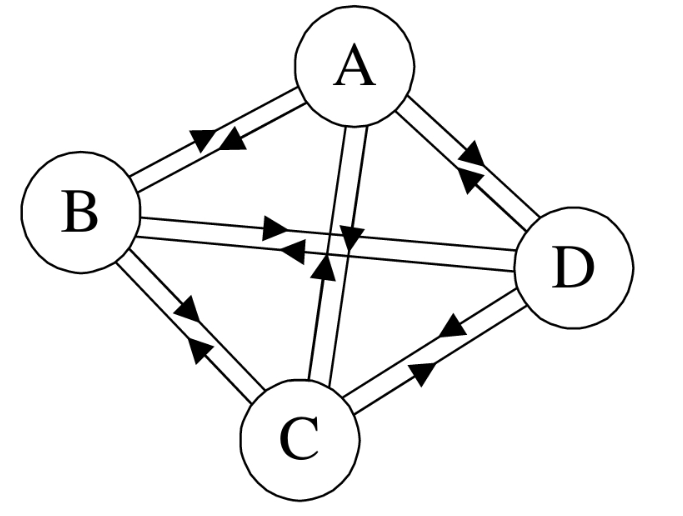
(3)按照边分为稀疏图和稠密图,当一个图的边数接近于完全图时,图称为稠密图,当一个图的边数较少时,这种图称为稀疏图,是一个相对概念。
(4)如果无重复的边或者顶点到自身的边叫简单图。在用数学方式表示时,无向边用()表示,有向边用<>表示。现在我们讲解的图全是简单图。
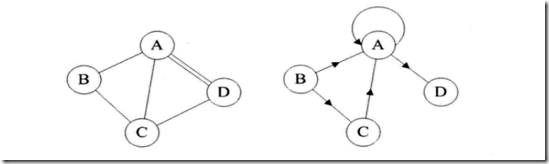
左图没有重复的边或者到自身的边(简单图),右图则有。
(5)边带权值的图叫网
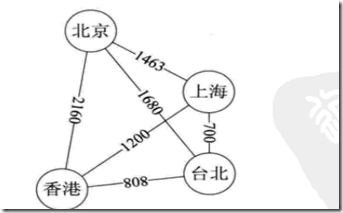
3、图的定点和边的关系
顶点的度:顶点关联边的数目。有向图图中有,入度:方向指向顶点的边;出度:方向背向顶点的边。在有向图中顶点的度就是两者之和。
路径长度:路径上边或者弧的数目。
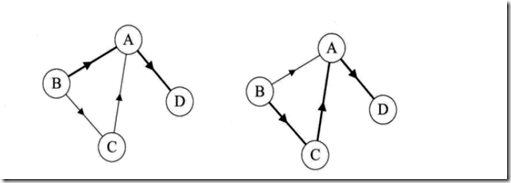
左图中,从B到D的路径度为2,在右图中就是3了(粗线的边)。
右图中A的入度是2,出度是1;B的入度为0,出度是2.
邻接:
①若无向图中的两个顶点V1和V2存在一条边(V1,V2),则称顶点V1和V2邻接(Adjacent);
②若有向图中存在一条边<V3,V2>,则称顶点V3与顶点V2邻接,且是V3邻接到V2或V2邻接直V3;
连通:
若从Vi到Vj有路径可通,则称顶点Vi和顶点Vj是连通(Connected)的。
无向图G中,任意两个顶点是相通的就是连通图。,有向则称为强连通图。
参考资料:
https://www.cnblogs.com/polly333/p/4760275.html
https://www.cnblogs.com/xiaobingqianrui/p/8902111.html