原文地址:https://blog.csdn.net/qq_39521554/article/details/79835515
利用泛函分析中的定义,设f是集合m到M的一个映射,用f(m)代表m在映射下的像的全体,如果f(m)=M,则映射f就称满射。如果m中的元素的像一定不同,那么映射f就称单射。如果既是满射又单射,就是一一映射。
单射(injection):每一个x都有唯一的y与之对应
满射(surjection):每一个y都必有至少一个x与之对应
双射(又叫一一对应,bijection): 同时满足单射与满射,也就是常见的函数映射
那么通俗的说,单射就是只能一对一,不能多对一,满射就是不论一对一,还是多对一,在映射f:X→Y中,Y中任一元素y都是X中某元素的像,也就是Y中所有元素在X中都能找到原像,至于找到的只有一个原像,那就是双射,但有的可以找到一个以上的那就不是双射,即双射就是既是单射又是满射。
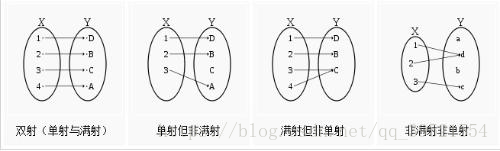
总之只能一对一或多对一,但不能一对多,并且在映射f:X→Y中X的每个元素都参与,Y中可能都参与,那就满了,就是满射,反之就不是满射。总之说的是一回事,没什么本质区别,只有联系。如果了解函数思想的同学可以试着将取值域,上域,以及定义域的关系带进来看一看