分治
- 全局( ightarrow)局部
地毯填补问题
题目描述
相传在一个古老的阿拉伯国家里,有一座宫殿。宫殿里有个四四方方的格子迷宫,国王选择驸马的方法非常特殊,也非常简单:公主就站在其中一个方格子上,只要谁能用地毯将除公主站立的地方外的所有地方盖上,美丽漂亮聪慧的公主就是他的人了。公主这一个方格不能用地毯盖住,毯子的形状有所规定,只能有四种选择(如图):
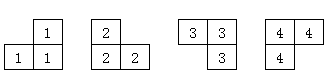
并且每一方格只能用一层地毯,迷宫的大小为(2^k imes2^k)的方形。当然,也不能让公主无限制的在那儿等,对吧?由于你使用的是计算机,所以实现时间为1s。
输入格式
输入文件共2行。
第一行:k,即给定被填补迷宫的大小为(2^k imes 2^k)(0<k≤10);
第二行:x,y,即给出公主所在方格的坐标(x 为行坐标,y 为列坐标),x 和 y 之间有一个空格隔开。
输出格式
将迷宫填补完整的方案:每一补(行)为x,y,c(x,y为毯子拐角的行坐标和列坐标,c为使用毯子的形状,具体见上面的图 1,毯子形状分别用 1,2,3,4 表示,x,y,c 之间用一个空格隔开)。
输入
3
3 3
输出
5 5 1
2 2 4
1 1 4
1 4 3
4 1 2
4 4 1
2 7 3
1 5 4
1 8 3
3 6 3
4 8 1
7 2 2
5 1 4
6 3 2
8 1 2
8 4 1
7 7 1
6 6 1
5 8 3
8 5 2
8 8 1
说明/提示
事实上感觉四个的形状分别是这样(仅供参考,如果有问题联系 icy)
注意:
c 越界
x,y 越界
mp[x][y] 已被占用
mp[x][y] 从未被使用。
#include<cstdio>
using namespace std;
#define ul dfs(a+l-1, b+l-1, a, b, l);
#define ur dfs(a+l-1, b+l, a, b+l, l);
#define dl dfs(a+l, b+l-1, a+l, b, l);
#define dr dfs(a+l, b+l, a+l, b+l, l);
int k,x,y;
void dfs(int x,int y,int a,int b,int l)
{
if (l==1) return;
l>>=1;
if (x-a>=l && y-b>=l)
{
printf("%d %d 4
", a+l-1, b+l-1);
ul
ur
dl
dfs(x, y, a+l, b+l, l);
}
if (x-a<l && y-b<l)
{
printf("%d %d 1
", a+l, b+l);
dfs(x,y,a,b,l);
ur
dl
dr
}
if (x-a>=l && y-b<l)
{
printf("%d %d 3
", a+l-1, b+l);
ul
ur
dfs(x, y, a+l, b, l);
dr
}
if (x-a<l && y-b>=l)
{
printf("%d %d 2
", a+l, b+l-1);
ul
dfs(x, y, a, b+l, l);
dl
dr
}
}
int main()
{
scanf("%d%d%d", &k, &x, &y);
dfs(x, y, 1, 1, 1<<k);
}
- 找好规律,比较简单。
逆序对
题目描述
猫猫TOM和小老鼠JERRY最近又较量上了,但是毕竟都是成年人,他们已经不喜欢再玩那种你追我赶的游戏,现在他们喜欢玩统计。最近,TOM老猫查阅到一个人类称之为“逆序对”的东西,这东西是这样定义的:对于给定的一段正整数序列,逆序对就是序列中ai>aj且i<j的有序对。知道这概念后,他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。
Update:数据已加强。
输入格式
第一行,一个数n,表示序列中有n个数。
第二行n个数,表示给定的序列。序列中每个数字不超过(10^9)
输出格式
给定序列中逆序对的数目。
输入
6
5 4 2 6 3 1
输出
11
说明/提示
对于25%的数据,(n≤2500)
对于50%的数据,(n≤4×10^4)
对于所有数据,(n≤5×10^5)
请使用较快的输入输出
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
int a[500005], r[500005], n;
long long ans;
void merge_sort(int s, int t)
{
if(s==t) return ;
int mid=(s+t)/2;
merge_sort(s, mid);
merge_sort(mid+1, t);
int i=s, j=mid+1, k=s;
while(i<=mid&&j<=t)
if(a[i]<=a[j]) r[k++]=a[i++];
else r[k++]=a[j++],ans+=(long long)mid-i+1;
while(i<=mid) r[k]=a[i],k++,i++;
while(j<=t) r[k]=a[j],k++,j++;
for(int i=s;i<=t;i++) a[i]=r[i];
}
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
}
merge_sort(1, n);
printf("%lld
", ans);
return 0;
}
-
归并排序