【图解数据结构】二叉树遍历

zoukankan html css js c++ java

【图解数据结构】二叉树遍历
目录
扯一扯
二叉树遍历原理
二叉树的创建
二叉树遍历方法
前序遍历
递归方式实现前序遍历
非递归方式实现前序遍历
中序遍历
递归方式实现中序遍历
非递归方式实现中序遍历
后序遍历
递归方式实现后序遍历
非递归方式实现后序遍历一
非递归方式实现后序遍历二
层序遍历
扯一扯

昨天在看《极客时间》严嘉伟老师的《如何做出好的职业选择——认识你的职业锚》专题直播时，严老师讲到了关于选择的一些问题，我认为其中的一些点讲的非常好，总结一下分享给大家。

人为什么难做选择？

选择意味着放弃

你选择一方，也就意味着放弃了另一方。摆在你面前的选择项越接近，你的选择就会越困难，因为放弃其中任何一个选择项都不容易。如果摆在你面前的选择项对比明显，那么选择起来就会轻松许多，大家几乎都会毫不犹豫的选择“好”的选择项，放弃掉“差”的选择项。

选择永远都不是完美的

选择永远都不可能十全十美，只可能满足尽量多的侧重点。选择的时候想满足越多的侧重点，可能就会越难做出选择。所以在选择上不要过于追求完美。

警惕逃避性选择——不知道自己要去哪儿，还要选择离开。

有一种选择是对现状不满，想逃离这种现状，但是却不知道去哪里。举个例子，可能目前的公司有各种问题，比如开发流程不规范等，如果因为这些问题离开，可能就会从一个坑跳到另外一个更大的坑。当决定离开的时候，一定是自己有明确的目标，很清楚自己想要什么。

二叉树遍历原理

二叉树的遍历是指从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。

为什么研究二叉树的遍历？

因为计算机只会处理线性序列，而我们研究遍历，就是把树中的结点变成某种意义的线性序列，这给程序的实现带来了好处。

二叉树的创建

遍历二叉树之前，首先我们要有一个二叉树。要创建一个如下图的二叉树，就要先进行二叉树的扩展，也就是将二叉树每个结点的空指针引出一个虚结点，其值为一个特定值，比如'#'。处理后的二叉树称为原二叉树的扩展二叉树。扩展二叉树的每个遍历序列可以确定一个一颗二叉树，我们采用前序遍历创建二叉树。前序遍历序列：124##5##36##7##。

定义二叉链表结点:
```
/// <summary>
/// 二叉链表结点类
/// </summary>
/// <typeparam name="T"></typeparam>
public class TreeNode<T>
{
    /// <summary>
    /// 数据域
    /// </summary>
    public T Data { get; set; }
    /// <summary>
    /// 左孩子   
    /// </summary>
    public TreeNode<T> LChild { get; set; } 
    /// <summary>
    /// 右孩子
    /// </summary>
    public TreeNode<T> RChild { get; set; } 

    public TreeNode(T val, TreeNode<T> lp, TreeNode<T> rp)
    {
        Data = val;
        LChild = lp;
        RChild = rp;
    }

    public TreeNode(TreeNode<T> lp, TreeNode<T> rp)
    {
        Data = default(T);
        LChild = lp;
        RChild = rp;
    }

    public TreeNode(T val)
    {
        Data = val;
        LChild = null;
        RChild = null;
    }

    public TreeNode()
    {
        Data = default(T);
        LChild = null;
        RChild = null;
    }
}
```
先序递归创建二叉树:
```
/// <summary>
/// 先序创建二叉树
/// </summary>
/// <param name="node"></param>
public static void CreateTree(TreeNode<char> node)
{
    node.Data = Console.ReadKey().KeyChar;

    if (node.Data == '#')
    {
        return;
    }

    node.LChild = new TreeNode<char>();

    CreateTree(node.LChild);

    if (node.LChild.Data == '#')
    {
        node.LChild = null;
    }

    node.RChild = new TreeNode<char>();

    CreateTree(node.RChild);

    if (node.RChild.Data == '#')
    {
        node.RChild = null;
    }
}
```
二叉树遍历方法

前序遍历

递归方式实现前序遍历
具体过程：

先访问根节点

再序遍历左子树

最后序遍历右子树
代码实现：
```
public static void PreOrderRecur(TreeNode<char> treeNode)
 {
     if (treeNode == null)
     {
         return;
     }
     Console.Write(treeNode.Data); 
     PreOrderRecur(treeNode.LChild);
     PreOrderRecur(treeNode.RChild);
 }
```
非递归方式实现前序遍历
具体过程：

首先申请一个新的栈，记为stack；

将头结点head压入stack中；

每次从stack中弹出栈顶节点，记为cur，然后打印cur值，如果cur右孩子不为空，则将右孩子压入栈中；如果cur的左孩子不为空，将其压入stack中；

重复步骤3，直到stack为空.
代码实现：
```
 public static void PreOrder(TreeNode<char> head)
{
    if (head == null)
    {
        return;
    }
    Stack<TreeNode<char>> stack = new Stack<TreeNode<char>>();
    stack.Push(head);
    while (!(stack.Count == 0))
    {
        TreeNode<char> cur = stack.Pop();
        Console.Write(cur.Data);

        if (cur.RChild != null)
        {
            stack.Push(cur.RChild);
        }
        if (cur.LChild != null)
        {
            stack.Push(cur.LChild);
        }
    }
}
```
过程模拟：

执行结果：

中序遍历

递归方式实现中序遍历
具体过程：

先中序遍历左子树

再访问根节点

最后中序遍历右子树
代码实现：
```
public static void InOrderRecur(TreeNode<char> treeNode)
{
    if (treeNode == null)
    {
        return;
    }  
    InOrderRecur(treeNode.LChild);
    Console.Write(treeNode.Data); 
    InOrderRecur(treeNode.RChild);
}
```
非递归方式实现中序遍历
具体过程：

申请一个新栈，记为stack，申请一个变量cur，初始时令cur为头节点；

先把cur节点压入栈中，对以cur节点为头的整棵子树来说，依次把整棵树的左子树压入栈中，即不断令cur=cur.left，然后重复步骤2；

不断重复步骤2，直到发现cur为空，此时从stack中弹出一个节点记为node，打印node的值，并让cur = node.right，然后继续重复步骤2；

当stack为空并且cur为空时结束。
代码实现：
```
public static void InOrder(TreeNode<char> treeNode)
{
    if (treeNode == null)
    {
        return;
    }
    Stack<TreeNode<char>> stack = new Stack<TreeNode<char>>();

    TreeNode<char> cur = treeNode;

    while (!(stack.Count == 0) || cur != null)
    {
        while (cur != null)
        {
            stack.Push(cur);
            cur = cur.LChild;
        }
        TreeNode<char> node = stack.Pop();
        Console.WriteLine(node.Data);
        cur = node.RChild;
    }
}
```
过程模拟：

执行结果：

后序遍历

递归方式实现后序遍历
先后序遍历左子树

再后序遍历右子树

最后访问根节点
代码实现：
```
public static void PosOrderRecur(TreeNode<char> treeNode)
{
    if (treeNode == null)
    {
        return;
    }
    PosOrderRecur(treeNode.LChild);
    PosOrderRecur(treeNode.RChild);
    Console.Write(treeNode.Data); 
}
```
非递归方式实现后序遍历一
具体过程：

使用两个栈实现

申请两个栈stack1，stack2，然后将头结点压入stack1中；

从stack1中弹出的节点记为cur，然后先把cur的左孩子压入stack1中，再把cur的右孩子压入stack1中；

在整个过程中，每一个从stack1中弹出的节点都放在第二个栈stack2中；

不断重复步骤2和步骤3，直到stack1为空，过程停止；

从stack2中依次弹出节点并打印，打印的顺序就是后序遍历的顺序；
代码实现：
```
public static void PosOrderOne(TreeNode<char> treeNode)
{
    if (treeNode == null)
    {
        return;
    }

    Stack<TreeNode<char>> stack1 = new Stack<TreeNode<char>>();
    Stack<TreeNode<char>> stack2 = new Stack<TreeNode<char>>();

    stack1.Push(treeNode);
    TreeNode<char> cur = treeNode;

    while (!(stack1.Count == 0))
    {
        cur = stack1.Pop();
        if (cur.LChild != null)
        {
            stack1.Push(cur.LChild);
        }
        if (cur.RChild != null)
        {
            stack1.Push(cur.RChild);
        }
        stack2.Push(cur);
    }

    while (!(stack2.Count == 0))
    {
        TreeNode<char> node = stack2.Pop();
        Console.WriteLine(node.Data); ;
    }
}
```
过程模拟：

执行结果：

非递归方式实现后序遍历二
具体过程：

使用一个栈实现

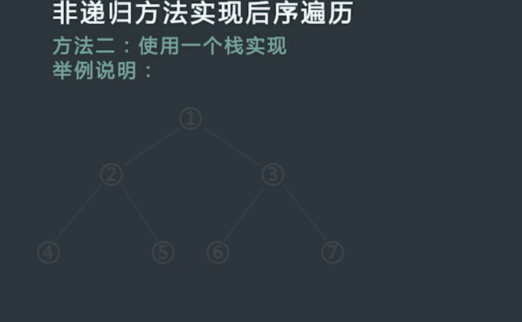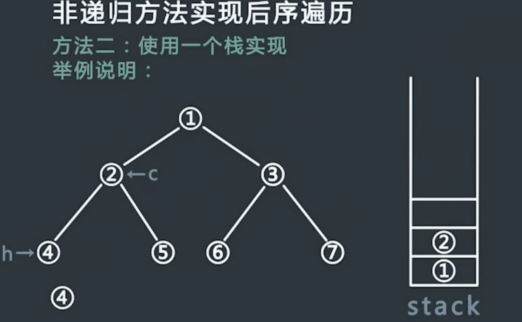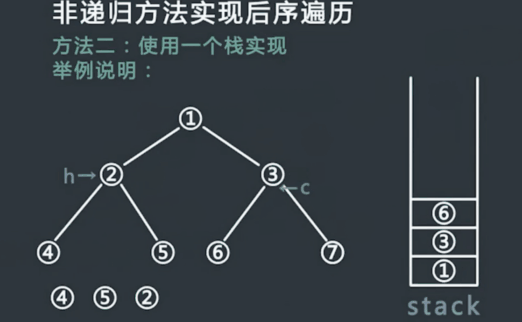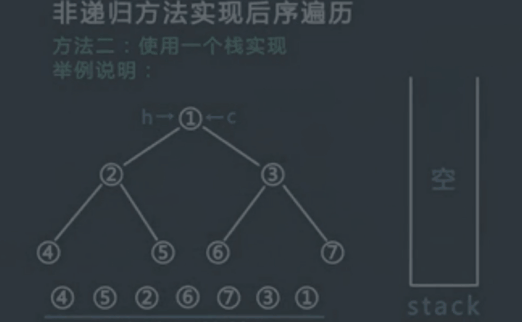
申请一个栈stack，将头节点压入stack，同时设置两个变量 h 和 c，在整个流程中，h代表最近一次弹出并打印的节点，c代表当前stack的栈顶节点，初始时令h为头节点，，c为null；

每次令c等于当前stack的栈顶节点，但是不从stack中弹出节点，此时分一下三种情况：

(1)如果c的左孩子不为空，并且h不等于c的左孩子，也不等于c的右孩子，则吧c的左孩子压入stack中

(2)如果情况1不成立，并且c的右孩子不为空，并且h不等于c的右孩子，则把c的右孩子压入stack中；

(3)如果情况1和2不成立，则从stack中弹出c并打印，然后令h等于c；

一直重复步骤2，直到stack为空.
代码实现：
```
public static void PosOrderTwo(TreeNode<char> treeNode)
{
    if (treeNode == null)
    {
        return;
    }

    Stack<TreeNode<char>> stack = new Stack<TreeNode<char>>();
    stack.Push(treeNode);

    TreeNode<char> h = treeNode;
    TreeNode<char> c = null;
    while (!(stack.Count == 0))
    {
        c = stack.Peek();
        //c结点有左孩子 并且 左孩子没被遍历（输出）过 并且 右孩子没被遍历过
        if (c.LChild != null && h != c.LChild && h != c.RChild)
            stack.Push(c.LChild);
        //c结点有右孩子 并且 右孩子没被遍历（输出）过
        else if (c.RChild != null && h != c.RChild)
            stack.Push(c.RChild);
        //c结点没有孩子结点 或者孩子结点已经被遍历（输出）过
        else
        {
            TreeNode<char> node = stack.Pop();
            Console.WriteLine(node.Data);
            h = c;
        }
    }
}
```
过程模拟：

执行结果：

层序遍历
具体过程：

首先申请一个新的队列，记为queue；

将头结点head压入queue中；

每次从queue中出队，记为node，然后打印node值，如果node左孩子不为空，则将左孩子入队；如果node的右孩子不为空，则将右孩子入队；

重复步骤3，直到queue为空。
代码实现：
```
public static void LevelOrder(TreeNode<char> treeNode)
{
    if(treeNode == null)
    {
         return;
    }
    Queue<TreeNode<char>> queue = new Queue<TreeNode<char>>();
    queue.Enqueue(treeNode);

    while (queue.Any())
    {
        TreeNode<char> node = queue.Dequeue();
        Console.Write(node.Data);

        if (node.Left != null)
        {
            queue.Enqueue(node.Left);
        }

        if (node.Right != null)
        {
            queue.Enqueue(node.Right);
        }
    }
}
```
执行结果：

参考：《大话数据结构》

作者：喜欢天黑却怕鬼

来源：http://songwenjie.cnblogs.com/

声明：本文为博主学习感悟总结，水平有限，如果不当，欢迎指正。如果您认为还不错，不妨点击一下下方的【推荐】按钮，谢谢支持。转载与引用请注明出处。
查看全文

相关阅读:
chrome浏览器解析xml
CuteEditor报错空引用错误
 猫哥网络编程系列：HTTP PEM 万能调试法
 猫哥网络编程系列：详解 BAT 面试题
 全新 Mac 安装指南（编程篇）（环境变量、Shell 终端、SSH 远程连接）
全新 Mac 安装指南（通用篇）（推荐设置、软件安装、推荐软件）
魅族手机浏览器兼容性调优最佳实践
 使用 nvm 管理不同版本的 node 与 npm
一种让 IE6/7/8 支持 media query 响应式设计的方法
 排列组合算法的javascript实现