重复性 重复性 重复性
找重复性、分解问题、然后解决问题
组合子问题
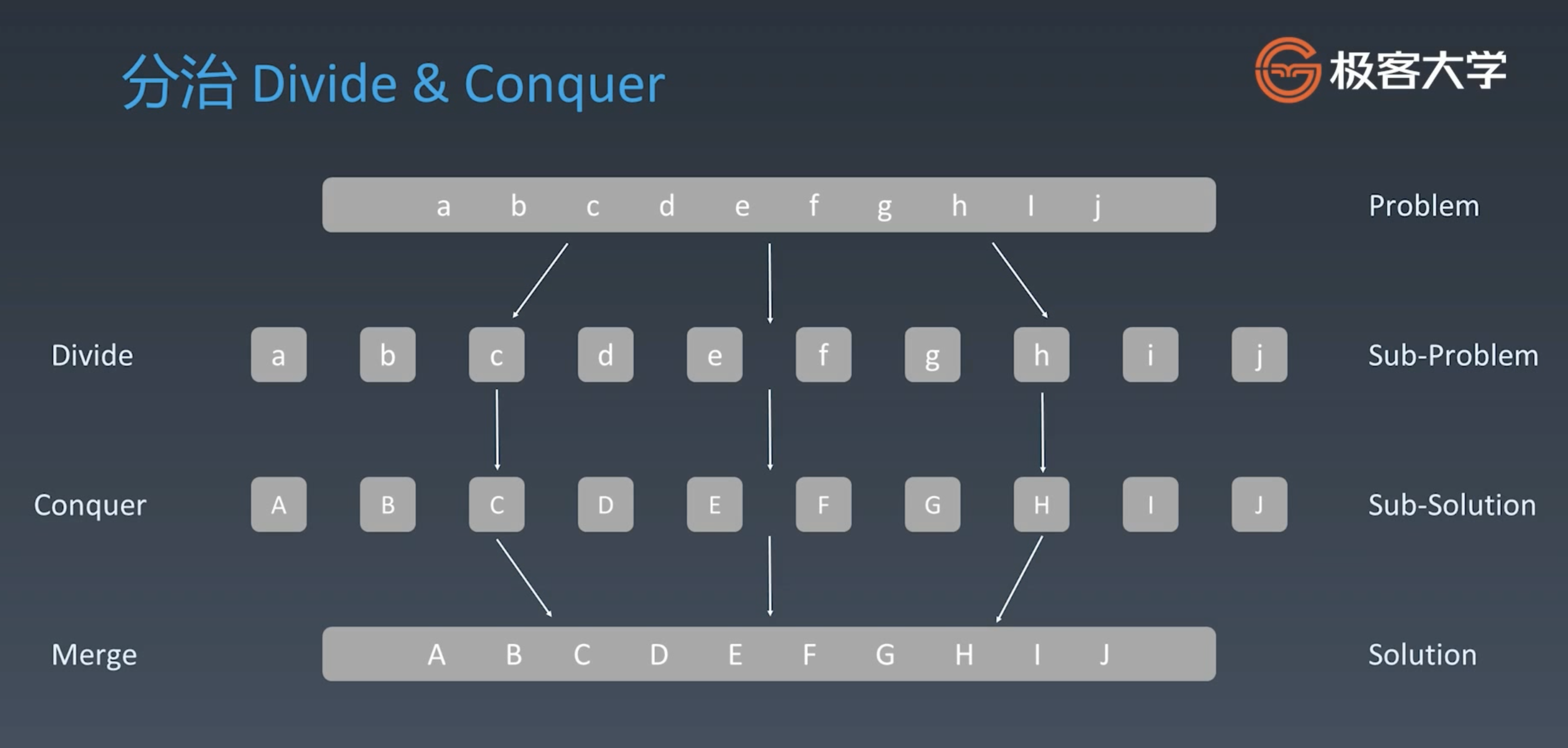
分治 DIvider & Conquer
python
def divide_conquer(problem, param1, param2, ...) {
# recursion terminator
if problem is None:
print_result;
return;
# prepare data
data = prepare_data(problem);
subproblems = split_problem(problem, data);
# conquer subproblems
subresult1 = self.divide_conquer(subproblems[0], p1, ...);
subresult2 = self.divide_conquer(subproblems[1], p1, ...);
subresult3 = self.divide_conquer(subproblems[2], p1, ...);
...
# process and generate the final result
result = process(subresult1, subresult2, subresult3., ..);
}
javascript
function divide_conquer(problem, param1, param2) {
// recursion terminator
if (problem === null) {
process result;
return;
}
// prepare data
data = preprare_data(problem);
subproblems = split_problem(problem, data);
// conquer subproblems
subresult1 = self.divide_conquer(subproblems[0], p1, ...);
subresult2 = self.divide_conquer(subproblems[1], p1, ...);
subresult3 = self.divide_conquer(subproblems[2], p1, ...);
// process and generate the final result
result = process_result(subresult1, subresult2, subresult3);
// revert the current level status
回溯
回溯法采用试错的思想,它尝试分步骤的去解决一个问题,在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确解答的时候,它将取消上一步甚至是上几步的计算,再通过其他的可能的分步解答再次尝试寻找问题的答案。
回溯法通常用最简单的递归方法来实现,在反复重复上述的步骤后可能出现两种情况:
- 找到一个可能存在的正确的答案
- 在尝试了所有可能的分步方法后宣告该问题没有答案
在最坏的情况下,回溯法会导致一次复杂度为指数时间的计算。