剑指offer刷题

 

题目描述：

输入一个链表，按链表从尾到头的顺序返回一个ArrayList。

思路：

这里用了一个数组reverse，但是实际可以用递归

# -*- coding:utf-8 -*-
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    # 返回从尾部到头部的列表值序列，例如[1,2,3]
    def printListFromTailToHead(self, listNode):
        l = []
        while listNode:
            l.append(listNode.val)
            listNode = listNode.next
        l.reverse()
        return l

题目描述：

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

思路：

因为是树的结构，一般都是用递归来实现。

用数学归纳法的思想就是，假设最后一步，就是root的左右子树都已经重建好了，那么我只要考虑将root的左右子树安上去即可。

根据前序遍历的性质，第一个元素必然就是root，那么下面的工作就是如何确定root的左右子树的范围。

根据中序遍历的性质，root元素前面都是root的左子树，后面都是root的右子树。那么我们只要找到中序遍历中root的位置，就可以确定好左右子树的范围。

正如上面所说，只需要将确定的左右子树安到root上即可。递归要注意出口，假设最后只有一个元素了，那么就要返回。

# -*- coding:utf-8 -*-
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def reConstructBinaryTree(self, pre, tin):
        # 递归终止条件
        if not pre and not tin:
            return
        # 树的根结点
        root = TreeNode(pre[0])
        # 根结点在中序遍历中的位置
        i = tin.index(pre[0])
        root.left = self.reConstructBinaryTree(pre[1:i+1], tin[:i])
        root.right = self.reConstructBinaryTree(pre[i+1:], tin[i+1:])
        return root

 

题目描述

用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

思路：

stack1输出给stack2，2一有就输出pop

# -*- coding:utf-8 -*-
class Solution:
    def __init__(self):
        self.stack1=[]
        self.stack2=[]
    def push(self, node):
        # write code here
        self.stack1.append(node)
    def pop(self):
        # return xx
        if self.stack2==[]:
            # stack1一旦装了就输出
            while self.stack1:
                self.stack2.append(self.stack1.pop())
            # 这里递归回来确保stack1 stack2是空的
            return self.stack2.pop()
        # 递归回来立刻输出
        return self.stack2.pop()

 

题目描述

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。

n<=39

思路：

背

# -*- coding:utf-8 -*-
class Solution:
    def Fibonacci(self, n):
        # write code here
        if n == 0:
            return 0
        if n == 1:
            return 1
        if n == 2:
            return 1
        if n >= 3:
            s = []*n
            s.append(1)
            s.append(1)
            for i in xrange(2,n):
                s.append(s[i-1]+s[i-2])
            return s[n-1]

 

题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

思路：

无论你跳多少，都是从1 2 层上去的

本质上是一个斐波那契数据

f(n) = f(n-1)+f(n-2)

# -*- coding:utf-8 -*-
class Solution:
    def jumpFloor(self,number):
        # write code here
        if (number <= 0) :
            return 0
        if (number == 1) :
            return 1
        if (number == 2) :
            return 2
        first = 1
        second = 2
        third = 0
        for i in range(3,number+1):
            third = first + second
            first = second
            second = third
        return third

 

题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

思路：

得出最终结论,在n阶台阶，一次有1、2、...n阶的跳的方式时，总得跳法为：

              | 1       ,(n=0 ) 

f(n) =     | 1       ,(n=1 )

              | 2*f(n-1),(n>=2)

（可以理解为最后一块板的选择是两种，踩或者不踩）

# -*- coding:utf-8 -*-
import math
class Solution:
    def jumpFloorII(self, number):
        # write code here
        if number <= 0:
            return 0
        else:
            number = number - 1
            return math.pow(2,number)
        # write code here

题目描述

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

 

比如n=3时，2*3的矩形块有3种覆盖方法：

我的思路，按着这个方式可以的，但是上面运行不通过，没搞懂

# -*- coding:utf-8 -*-
class Solution:
    def rectCover(self, number):
        # write code here
        if number <1:
            return 0
        elif number <=3:
            return number
        else:
            number = self.rectCover(number-1)+self.rectCover(number-2)
        return number

别人做法：

# -*- coding:utf-8 -*-
class Solution:
    def rectCover(self, number):
        # write code here
        if number < 1:
            return 0
        p = q = r =0
        for i in range(1,number+1):
            if i == 1:
                p = q = r =1
            elif i == 2:
                q = r = 2
            else:
                r = q + p
                p = q
                q = r
        return r

题目描述

输入一个链表，输出该链表中倒数第k个结点。

思路：

用一个数组装着，倒数K个，用的list[-k]

# -*- coding:utf-8 -*-
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
 
class Solution:
    def FindKthToTail(self, head, k):
        # write code here
        l=[]
        while head!=None:
            l.append(head)
            head=head.next
        if k>len(l) or k<1:
            return
        return l[-k]

题目描述

输入一个链表，反转链表后，输出新链表的表头。

思路：

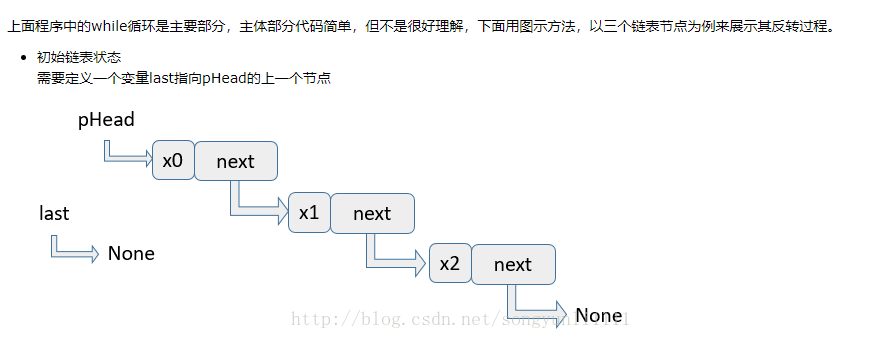
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    # 返回ListNode
    def ReverseList(self, pHead):
        # write code here
        if pHead is None:
            return pHead
        last = None  #指向上一个节点
        while pHead:
            # 先用tmp保存pHead的下一个节点的信息，
            # 保证单链表不会因为失去pHead节点的next而就此断裂
            tmp = pHead.next
            # 保存完next，就可以让pHead的next指向last了
            pHead.next = last
            # 让last，pHead依次向后移动一个节点，继续下一次的指针反转
            last = pHead
            pHead = tmp
        return last

题目描述

输入两个单调递增的链表，输出两个链表合成后的链表，当然我们需要合成后的链表满足单调不减规则。

思路：

就是另外生成一个链表去匹配

# -*- coding:utf-8 -*-
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
 
class Solution:
    # 返回合并后列表
    def Merge(self, pHead1, pHead2):
        # write code here
        mergeHead = ListNode(90)
        # 这里是把头指针给了p
        p = mergeHead
        while pHead1 and pHead2:
            if pHead1.val >= pHead2.val:
                mergeHead.next = pHead2
                pHead2 = pHead2.next
            else:
                mergeHead.next = pHead1
                pHead1 = pHead1.next
                  
            mergeHead = mergeHead.next
        # 看看1和2哪个还没走完的
        if pHead1:
            mergeHead.next = pHead1
        elif pHead2:
            mergeHead.next = pHead2
        return p.next
                 

题目描述

输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构）

思路：

递归下去，到最后一个结点

链接：https://www.nowcoder.com/questionTerminal/6e196c44c7004d15b1610b9afca8bd88
来源：牛客网

public class Solution {
    public static boolean HasSubtree(TreeNode root1, TreeNode root2) {
        boolean result = false;
        //当Tree1和Tree2都不为零的时候，才进行比较。否则直接返回false
        if (root2 != null && root1 != null) {
            //如果找到了对应Tree2的根节点的点
            if(root1.val == root2.val){
                //以这个根节点为为起点判断是否包含Tree2
                result = doesTree1HaveTree2(root1,root2);
            }
            //如果找不到，那么就再去root的左儿子当作起点，去判断时候包含Tree2
            if (!result) {
                result = HasSubtree(root1.left,root2);
            }
             
            //如果还找不到，那么就再去root的右儿子当作起点，去判断时候包含Tree2
            if (!result) {
                result = HasSubtree(root1.right,root2);
               }
            }
            //返回结果
        return result;
    }
 
    public static boolean doesTree1HaveTree2(TreeNode node1, TreeNode node2) {
        //如果Tree2已经遍历完了都能对应的上，返回true
        if (node2 == null) {
            return true;
        }
        //如果Tree2还没有遍历完，Tree1却遍历完了。返回false
        if (node1 == null) {
            return false;
        }
        //如果其中有一个点没有对应上，返回false
        if (node1.val != node2.val) {  
                return false;
        }
         
        //如果根节点对应的上，那么就分别去子节点里面匹配
        return doesTree1HaveTree2(node1.left,node2.left) && doesTree1HaveTree2(node1.right,node2.right);
    }

# -*- coding:utf-8 -*-
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    # 返回镜像树的根节点
    def Mirror(self, root):
        # write code here
        if root!=None:
            root.left,root.right=root.right,root.left
            self.Mirror(root.left)
            self.Mirror(root.right)

题目描述

定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的min函数（时间复杂度应为O（1））。

注意：保证测试中不会当栈为空的时候，对栈调用pop()或者min()或者top()方法。

思路：

用一个栈data保存数据，用另外一个栈min保存依次入栈最小的数

比如，data中依次入栈，5,  4,  3, 8, 10, 11, 12, 1

  则min依次入栈，5,  4,  3，no,no, no, no, 1

no代表此次不如栈

每次入栈的时候，如果入栈的元素比min中的栈顶元素小或等于则入栈，否则不如栈。

# -*- coding:utf-8 -*-
class Solution:
    def __init__(self):
        # 定义两个栈，其中一个是装小点的
        self.stack = []
        self.min_stack = []
    def push(self, node):
        # write code here
        self.stack.append(node)
        if(not self.min_stack or node <= self.min_stack[-1]):
            self.min_stack.append(node)
    def pop(self):
        # write code here
        if(self.stack[-1] == self.min_stack[-1]):
            self.min_stack.pop()
        return self.stack.pop()
    def top(self):
        # write code here
        return self.stack[-1]
    def min(self):
        # write code here
        return self.min_stack[-1]

题目描述

从上往下打印出二叉树的每个节点，同层节点从左至右打印。

思路：

递归

def PrintFromTopToBottom(self, root):
        if not root:
            return []
        currentStack = [root]
        res = []
        while currentStack:
            nextStack = []
            for i in currentStack:
                if i.left: nextStack.append(i.left)
                if i.right: nextStack.append(i.right)
                res.append(i.val)
            currentStack = nextStack
        return res

题目描述

二叉树的前序、中序、后序遍历 python

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
class Solution:
    #前序
    def preorder(self,root,ans=[]):
        if root!=None:
            ans.append(root.val)
        if root.left:
            self.preorder(root.left,ans)
        if root.right:
            self.preorder(root.right,ans)
        return ans
    
    #中序
    def inorder(self,root,ans=[]):
        # if root.left==None and root.right==None:
        #     ans.append(root.val)
        #     return
        if root.left:
            self.inorder(root.left,ans)
        ans.append(root.val)
        if root.right:
            self.inorder(root.right,ans)
        return ans
    
    #后序
    def postorder(self,root,ans=[]):
        if root.left:
            self.postorder(root.left,ans)
        if root.right:
            self.postorder(root.right,ans)
        ans.append(root.val)
        return ans

　

题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

思路：

把左子树、右子树的状态都设置为布尔值，递归两边，判断是不是都符合左小右大的规则

python:后序遍历 的序列中，最后一个数字是树的根节点 ，数组中前面的数字可以分为两部分：第一部分是左子树节点 的值，都比根节点的值小；第二部分 是右子树 节点的值，都比 根 节点 的值大，后面用递归分别判断前后两部分 是否 符合以上原则

class Solution:
    def VerifySquenceOfBST(self, sequence):
        # write code here
        if sequence==None or len(sequence)==0:
            return False
        length=len(sequence)
        root=sequence[length-1]
        # 在二叉搜索 树中 左子树节点小于根节点
        for i in range(length):
            if sequence[i]>root:
                break
        # 二叉搜索树中右子树的节点都大于根节点
        for j  in range(i,length):
            if sequence[j]<root:
                return False
        # 判断左子树是否为二叉树
        left=True
        if  i>0:
            left=self.VerifySquenceOfBST(sequence[0:i])
        # 判断 右子树是否为二叉树
        right=True
        if i<length-1:
            right=self.VerifySquenceOfBST(sequence[i:-1])
        return left and right

题目描述

输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。

思路：

排列组合常用工具

import itertools

itertools.permutations（str）

# -*- coding:utf-8 -*-
import itertools
 
class Solution:
    def Permutation(self, ss):
        # write code here
        if not ss:
            return ss
        result = []
        k = itertools.permutations(ss)
        for i in k:
            result.append(''.join(i))
        result = list(set(result))
        # 一定要排序才能过
        result.sort()
        return result

题目描述

输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4,。

最简单的题，卡进了莫名的BUG。。不能全部AC

# -*- coding:utf-8 -*-
class Solution:
    def GetLeastNumbers_Solution(self, tinput, k):
        # write code here
        if tinput is None:
            return
        n = len(tinput)
        if n < k:
            return []
        tinput = sorted(tinput)
        return tinput[:k]

题目描述

求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数？为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数（从1 到 n 中1出现的次数）。

 思路：

掌握str.count(i) 可以查找字符串中元素个数

# -*- coding:utf-8 -*-
class Solution:
    def NumberOf1Between1AndN_Solution(self, n):
        # write code here
        a = 0
        for i in range(0, n+1):
            if ('1' in str(i)):
                ind = str(i).count('1')
                a+= ind
            else:
                pass
        return a

题目描述

把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。

# -*- coding:utf-8 -*-
class Solution:
    def PrintMinNumber(self, numbers):
        # write code here
        temp = [str(x) for x in sorted(numbers, cmp=self.f_cmp)]
        return ''.join(temp)
         
    def f_cmp(self,a,b):
        if str(a)+str(b) < str(b)+str(a):
            return -1
        elif str(a)+str(b) > str(b)+str(a):
            return 1
        else:
            return 0

题目描述

在一个字符串(0<=字符串长度<=10000，全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1（需要区分大小写）.

# -*- coding:utf-8 -*-
class Solution():
    def FirstNotRepeatingChar(self, s):
        dict_n = {}
        simple_list = []
        for i in s:
            if(i not in dict_n):
                dict_n[i] = 1
            else:
                dict_n[i]+=1
        for i in dict_n:
            if(dict_n[i]==1):
                simple_list.append(i)

        start_pos = []
        if(len(simple_list)):
            for j in simple_list:
                ind = s.index(j)
                start_pos.append(ind)
            start_pos.sort()
            return start_pos[0]
        else:
            return -1

题目描述

输入两个链表，找出它们的第一个公共结点。（注意因为传入数据是链表，所以错误测试数据的提示是用其他方式显示的，保证传入数据是正确的）

思路：

通过结点的值相同，确定这个就是公共节点，返回node即可

# -*- coding:utf-8 -*-
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
  
class Solution:
    def FindFirstCommonNode(self, head1, head2):
        # write code here
        list1 = []
        list2 = []
        node1 = head1
        node2 = head2
        while node1:
            list1.append(node1.val)
            node1 = node1.next
        while node2:
            if node2.val in list1:
                return node2
            else:
                node2 = node2.next

题目描述

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。

思路：

其实就是深度遍历，用递归的方法可以了。递归求解：
假如是空节点，则返回0；
否则，原树的深度由左右子树中深度较的深度加1，为原树的深度。

# -*- coding:utf-8 -*-
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def TreeDepth(self, pRoot):
        # write code here
        if not pRoot:
            return 0
        return max(1 + self.TreeDepth(pRoot.left), 1 + self.TreeDepth(pRoot.right))

题目描述

输入一棵二叉树，判断该二叉树是否是平衡二叉树。

思路：先判断两棵树的最深高度是多少，如果一样就继续，一层层递归下去，确保每一颗子树都一样

# -*- coding:utf-8 -*-
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def IsBalanced_Solution(self, pRoot):
        # write code here
        if not pRoot:
            return True
        # 如果两边的树不是一样高，就不是平衡树
        a = abs(self.TreeDepth(pRoot.left) - self.TreeDepth(pRoot.right))
        if(a>1):
            return False
        # 这一步容易漏，要确保递归到每一个子树（左右）都是平衡的
        return self.IsBalanced_Solution(pRoot.left) and self.IsBalanced_Solution(pRoot.right)
        
    def TreeDepth(self, pRoot):
        # 这里是上一题的最大深度，用来求左右子树的最大
        if not pRoot:
            return 0
        left_ = 1 + self.TreeDepth(pRoot.left)
        right_ = 1 + self.TreeDepth(pRoot.right)
        return max(left_, right_)

题目描述

输入一个递增排序的数组和一个数字S，在数组中查找两个数，使得他们的和正好是S，如果有多对数字的和等于S，输出两个数的乘积最小的。

输出描述:

对应每个测试案例，输出两个数，小的先输出.

# -*- coding:utf-8 -*-
import itertools
class Solution:
    def FindNumbersWithSum(self, array, tsum):
        if(array.__len__()==0):
            return array
        tsum_list =[]
        dix_ = 0
        result = []
        for i in itertools.permutations(array,2):
            if(i[0]+i[1]==tsum):
                tsum_list.append(i)
        for i in tsum_list:

            if(dix_==0):
                dix_ = i[0] * i[1]
                result = [min(i[0], i[1]), max(i[0], i[1])]

            elif(i[0]*i[1]<dix_):
                dix_ = i[0]*i[1]
                result = [min(i[0],i[1]),max(i[0],i[1])]

        return result

题目描述

对于一个给定的字符序列S，请你把其循环左移K位后的序列输出。字符序列S=”abcXYZdef”,要求输出循环左移3位后的结果，即“XYZdefabc”。是不是很简单？OK，搞定它！

思路：采用序列拼接，机智！

# -*- coding:utf-8 -*-
class Solution:
    def LeftRotateString(self, s, n):
        # write code here
        return s[n:]+s[:n]

题目描述

字符串翻转思路

注意，用reverse,lst[::-1]都可以

        # -*- coding:utf-8 -*-
class Solution:
    def ReverseSentence(self, s):
        # write code here
        l=s.split(' ')
        return ' '.join(l[::-1])

题目描述

求1+2+3+...+n，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

思路：不能用循环，那就递归解决吧！

# -*- coding:utf-8 -*-
class Solution:
    def __init__(self):
        self.a = 0
    def Sum_Solution(self, n):
        if n==0:
            return self.a
        else:
            self.a += n
            return self.Sum_Solution(n-1)

题目描述

写一个函数，求两个整数之和，要求在函数体内不得使用+、-、*、/四则运算符号。

思路：本意是想让我们掌握01计算

public class Solution {
    public int Add(int num1,int num2) {
        while (num2!=0) {
            int temp = num1^num2;
            num2 = (num1&num2)<<1;
            num1 = temp;
        }
        return num1;
    }
}

题目描述

请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。

思路：

一开始想用一个list装着中序遍历+后续遍历，但是这样只能证明两边是一样的，不是对称的。

因此，还是用递归的方法，一个个节点比较下去

# -*- coding:utf-8 -*-
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def isSymmetrical(self, pRoot):
        # write code here
        def is_same(p1,p2):
            # 确保只有一个根节点的情况
            if not p1 and not p2:
                return True
            if (p1 and p2) and p1.val==p2.val:
                # 镜像的问题
                return is_same(p1.left,p2.right) and is_same(p1.right,p2.left)
            return False
        if not pRoot:
            # 确保没有结点的情况
            return True
        # 下面都是不对称的第一步判断
        if pRoot.left and not pRoot.right:
            return False
        if not pRoot.left and pRoot.right:
            return False
        # 递归下去子树
        return is_same(pRoot.left,pRoot.right)
            

题目描述

给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。

例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}；

针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。

# -*- coding:utf-8 -*-
class Solution:
    def maxInWindows(self, num, size):
        # write code here
        if size <= 0:
            return []
        res = []
        for i in xrange(0, len(num)-size+1):
            res.append(max(num[i:i+size]))
        return res

题目描述

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。

路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。

如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。

例如 

矩阵中包含一条字符串"bcced"的路径，但是矩阵中不包含"abcb"路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

思路：

回溯法还不是很熟，这里用深度优先遍历方法解决

# -*- coding:utf-8 -*-
class Solution:
    # 基于深度优先遍历的方法
    # 与原本的深度遍历不同的地方在于，除了当前路径的节点被标记为DISCOVERED，其他路径上的节点撤销该标记
    def hasPath(self, matrix, rows, cols, path):
        # write code here
        self.discovered = {} # 维护矩阵中的节点是否遍历
        self.tar = 0 # 维护要遍历到的path的位置
        matrix = list(matrix)
        matrix = [matrix[i*cols:i*cols+cols] for i in range(rows)] # 将输入的字符串复原为矩阵
        def dfs(x,y): # 深度优先遍历的子函数，只有在遍历刚好结束于path的最后一个字符也相等的时候，返回TRUE
            if x<0 or x==rows or y<0 or y==cols: # 如果坐标非法
                return False
            if (x,y) in self.discovered or matrix[x][y] != path[self.tar]: # 如果坐标已被访问或者坐标与应匹配字符串不同
                return False
            # 如果坐标合法且匹配正确
            if self.tar == len(path) - 1: # 如果已经匹配到了最后一个字符
                return True
            # 匹配到中间字符，则继续向下遍历
            self.discovered[x,y] = 1 # 标记当前坐标，防止重复访问
            self.tar += 1 # 向后移动匹配位置
            ret = dfs(x-1,y) or dfs(x+1,y) or dfs(x,y-1) or dfs(x,y+1) # 向四个方向进行深度优先遍历，确定匹配最终结果
            # 当遍历返回的时候，重置该坐标的访问标志和path的匹配位置
            self.discovered.pop((x,y))
            self.tar -= 1
            return ret
        # 依次将每一个单元格作为遍历起点
        for i in range(rows):
            for j in range(cols):
                if dfs(i,j):
                    return True
        return False

题目描述

从上到下按层打印二叉树，同一层结点从左至右输出。每一层输出一行。

思路：

层次遍历，加多了一个list【【第一行】，【第二行】】

# -*- coding:utf-8 -*-
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    # 返回二维列表[[1,2],[4,5]]
    def Print(self, pRoot):
        # write code here
        if not pRoot:
            return []
        res=[]
        tmp=[pRoot]
        while tmp:
            size=len(tmp)
            row=[]
            for i in tmp:
                row.append(i.val)
            res.append(row)
            for i in range(size):
                node=tmp.pop(0)
                if node.left:
                    tmp.append(node.left)
                if node.right:
                    tmp.append(node.right)
        return res

题目描述

给定一棵二叉搜索树，请找出其中的第k小的结点。例如， （5，3，7，2，4，6，8）    中，按结点数值大小顺序第三小结点的值为4。

思路：

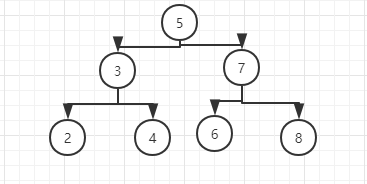
#前序遍历5324768
#中序遍历2345678
#后序遍历2436875   对于二叉搜索树来说，中序遍历就是从小到大的顺序，所以用一个list装着，然后输出list[k-1]即可

# -*- coding:utf-8 -*-
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    # 返回对应节点TreeNode
    def KthNode(self, pRoot, k):
        # write code here
        #第三个节点是4
        #前序遍历5324768
        #中序遍历2345678
        #后序遍历2436875
        #所以是中序遍历，左根右
        global result
        result=[]
        self.midnode(pRoot)
        if  k<=0 or len(result)<k:
            return None
        else:
            return result[k-1]
              
    def midnode(self,root):
        if not root:
            return None
        self.midnode(root.left)
        result.append(root)
        self.midnode(root.right)

题目描述

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。

如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，使用GetMedian()方法获取当前读取数据的中位数。

思路：

通过length%2==0 来判断奇数偶数

# -*- coding:utf-8 -*-
class Solution:
    def __init__(self):
        self.data=[]
    def Insert(self, num):
        # write code here
        self.data.append(num)
        self.data.sort()
    def GetMedian(self,data):
        # write code here
        length=len(self.data)
        if length%2==0:
            return (self.data[length//2]+self.data[length//2-1])/2.0
        else:
            return self.data[int(length//2)]

题目描述

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。

假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。

（注意：这两个序列的长度是相等的）

思路：

采用一个辅助栈。

【思路】借用一个辅助的栈，遍历压栈顺序，先讲第一个放入栈中，这里是1，然后判断栈顶元素是不是出栈顺序的第一个元素，这里是4，很显然1≠4，所以我们继续压栈，直到相等以后开始出栈，出栈一个元素，则将出栈顺序向后移动一位，直到不相等，这样循环等压栈顺序遍历完成，如果辅助栈还不为空，说明弹出序列不是该栈的弹出顺序。

举例：

入栈1,2,3,4,5

出栈4,5,3,2,1

首先1入辅助栈，此时栈顶1≠4，继续入栈2

此时栈顶2≠4，继续入栈3

此时栈顶3≠4，继续入栈4

此时栈顶4＝4，出栈4，弹出序列向后一位，此时为5，,辅助栈里面是1,2,3

此时栈顶3≠5，继续入栈5

此时栈顶5=5，出栈5,弹出序列向后一位，此时为3，,辅助栈里面是1,2,3

….

依次执行，最后辅助栈为空。如果不为空说明弹出序列不是该栈的弹出顺序。

import java.util.ArrayList;
import java.util.Stack;
public class Solution {
    public boolean IsPopOrder(int [] pushA,int [] popA) {
        if(pushA.length == 0 || popA.length == 0)
            return false;
        Stack<Integer> s = new Stack<Integer>();
        //用于标识弹出序列的位置
        int popIndex = 0;
        for(int i = 0; i< pushA.length;i++){
            s.push(pushA[i]);
            //如果栈不为空，且栈顶元素等于弹出序列
            while(!s.empty() &&s.peek() == popA[popIndex]){
                //出栈
                s.pop();
                //弹出序列向后一位
                popIndex++;
            }
        }
        return s.empty();
    }
}