《概率统计》2.离散型随机变量：分布与数字特征

从事件到随机变量

我们可以把某一次具体试验中所有可能出现的结果构成一个样本空间，对于样本空间中的每一个可能的试验结果，我们去将他关联到一个特定的数。这种试验结果与数的对应关系就形成了随机变量，将试验结果所对应的数称为随机变量的取值。这里就是接下来要讨论的重要内容。

请注意这个概念中的一个关键点，随机变量如何取值？他可以直接就是试验的结果取值，比如“抛掷骰子的结果点数为 5”。

但是，随机变量更多的是这种情况，比如随机变量可以是“连续抛掷硬币 10 次，其中硬币正面出现的次数”，或者是映射值：我们把骰子连续抛掷两次，随机变量对应连续两次试验中的最大值或者点数之和，这就是映射的情况。但是无论如何，对于随机变量，都必须要明确对应具体的取值。

离散型随机变量及其要素

很容易联想到，随机变量作为一种映射后的取值，本质上和函数取值一样，可以有连续型和离散型两种，在这一篇博客里，我们主要讨论离散型的情况和应用场景，连续型的情况放在下一篇来讲解。

对于连续和离散的概念，大家脑海里的直观印象往往更加简单，但具体怎么用形式化的概念语言来描述他，反而要更繁琐一些。我们还是严格的对离散型随机变量做一个定义，即：随机变量的取值只能是有限多个或者是可数的无限多个值。

那么对于任意的我们获取的一组随机变量，最关注的是哪些要素呢？我们来列举一下：

第一：随机变量的取值。 显然这个是我们首先需要关注的，由试验结果派生出的这一组随机变量到底能取到哪些值，这是我们首要关注的问题点。

第二：试验中每个对应取值的概率。 每个事件的结果肯定不是等概率的，这也恰恰就是我们研究的出发点。

第三：随机变量的统计特征和度量方法。 弄清楚随机变量每一个具体的取值，我们把握的是他的个体特征，那么如何从整体上来把握这一组随机变量的统计特征呢？这也是非常重要的。

结合三个问题，来讨论一下离散型随机变量的分布

分布列描述的就是离散型随机变量每一种取值及其对应的概率，随机变量一般用大写字母表示，其具体的取值一般用小写字母来表示。例如，随机变量X的分布列，我们一般用P_X来表示，而x来表示随机变量X的某个具体的取值，因此把上述信息结合起来就有：

随机变量 X 取值为 x 的概率，本质上也是一个事件的概率，这个事件就是 {X=x}，我们将他记作：P_X(x)或者P({X=x})

为了更清楚的解释这个式子，我们还是回到抛硬币这个最简单的情况中来。随机变量 X 表示两次抛掷硬币正面向上的次数，随机变量 X 的分布列如下表所示：

从上面的随机变量分布列中我们可以清晰地看出随机变量 X 的每一种取值以及所对应的取值概率。例如，正面向上的次数为 1 时，对应的事件概率为 1/2。这个分布列虽然非常简单，但是麻雀虽小五脏俱全，下面我们来重点关注里面最重要的两个要点。

第一，对于随机变量 X 的所有可能取值，其概率之和为 1，表示成表达式就是：∑_xP_X(x) = 1

第二，对于随机变量 X 的不同取值 x，对应的事件 {X=x} 彼此之间是互不相容的。因此多个事件构成的事件集合 S 的发生概率，可以通过对应事件发生的概率直接相加得到。即:P(X ∈ S)=∑_x∈SP_x(x)

举个例子：比如我们想计算一下连续两次抛掷硬币，出现正面向上的概率为多大，这个事件集合实际上包含了两个事件：事件 1 是 {X=1}，事件 2 是 {X=2}，二者彼此是互不相容的，我们按照上面的式子可以得出其概率：P(X > 0) = P_X(1) + P_X(2) = 3 / 4

分布列和概率质量函数(PMF)

一般情况下，我们最好是结合图形来观察一个随机变量的分布，这样一来，他的特性就能够非常直观的展现出来。

这里，就不得不提一下概率质量函数（PMF），概率质量函数就是将随机变量的每个值映射到其概率上，看上去和分布列就是一回事儿。

二项分布及二项随机变量

我们还是举抛硬币的例子：将一个硬币抛掷 n 次，每次抛掷出现正面的概率为 p，每次抛掷彼此之间都是相互独立的，随机变量 X 对应 n 次抛掷中、得到的是正面的次数。

这里，随机变量 X 服从二项分布(结果要么发生、要么不发生)，二项分布中的核心参数就是上面提到的 n 和 p，随机变量的分布列可以通过下面这个熟悉的公式计算得到：

P_x(k) = p^k(1-p)^n-k，其中k为抛掷n次硬币、结果出现的是正面的次数，显然k=0,1,2...n

服从二项分布的随机变量，他的期望和方差的表示很简单，服从参数为 (n,p) 的二项分布的随机变量 X，他的期望和方差的公式我们直接给出来：

期望：E(X) = np

方差：V(X) = np(1 - p)

几何分布与几何随机变量

我们在二项分布的基础上再来介绍几何分布，在连续抛掷硬币的试验中，每次抛掷出现正面的概率为 p，出现反面的概率为 1−p，在这种背景下，几何随机变量 X 就用来表示连续抛掷硬币直到第一次出现正面所需要的抛掷次数。

或者我们再举一个直白点的例子，学校里有 10 个白富美女生（假定她们互相不认识，保证独立性），你依次去找她们表白，只要有一个成功了，你就结束了单身狗的日子。但是表白成功的概率为 p，当然，成功的概率肯定不大，但是你秉持着死皮赖脸、死缠烂打，不成功誓不罢休的精神，只要女神拒绝你的表白，就换一个女神继续表白，直到某一个女神答应你为止，那么你一共表白过的总的次数，就是几何型的随机变量。

总结一下，几何分布的期望和方差分别为：

• E(X) = 1 / p
• V(X) = (1 - p) / p²

泊松分布及泊松随机变量

首先我们提一下什么是伯努利试验：在同样的条件下、相互独立地进行的一种随机试验就叫做伯努利试验，其特点就是实验结果是有两种可能：发生或者不发生。我们假设该试验独立重复地进行了n次，那么我们就称这一系列重复独立的随机试验为n重伯努利试验、或者伯努利概型。所以单个伯努利试验是没有多大意义的，然而，当我们反复进行伯努利试验，去观察这些试验有多少是成功的，多少是失败的，事情就变得有意义了，这些累计记录包含了很多潜在的非常有用的信息。

所以我们上面的抛硬币试验就属于伯努利试验

我们看到，n次独立的伯努利试验成功的次数是一个服从二项分布的随机变量，其中参数为n和p，n为试验重复的次数，p为发生的概率，然后我们说期望为np。但如果n非常大、p非常小呢，得到np依旧是适中的，但这很明显是值得我们分析的

现实生活中有没有这类情况？有，比如我们考虑任何一天内发生飞机事故的总数，记作随机变量 X，总共飞机飞行的次数 n 非常大，但是单架次飞机出现事故的概率 p 非常小。或者用随机变量 X 表示一本书中字印刷错误的次数，n 表示一本书中的总字数，非常大，而 p 表示每个字印刷出错的概率，非常小。

这种情况下，n 很大 p 很小，二项分布的分布列可以简化为我们这里谈到的泊松分布的分布列：

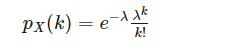
其中，λ=np，k=0,1,2,3...

期望和方差满足：

• E(X) = λ
• V(X) = λ

特别的，当我们的 n→∞、且p = λ/n趋近于0时，对应的二项分布列：P_x(k) = p^k(1-p)^n-k就收敛于上面的泊松分布列了。

通俗点说，就是只要当λ=np，且n非常大、p非常小，泊松分布就是二项分布的一个非常好的近似，计算简便是它的一大很大的优势。