面向对象_方法_例题

java书P103,c#书P153
注意：现阶段，忽略一切修饰符
先阅读文字，别看例程
---------------------------------
基础：喊人程序
say_hi()
say_hi("刘阿姨")
返回say_hi("刘阿姨")
总结：方法基本用法

【格式】 返回值类型 方法名称（参数）

{

　　【方法内容】

　　return 返回值;

}
------------------------------
最大值2

练习：编写四个方法，分别求两个数的和差积商，并运用。

思考题：编写以下方法，并调用

输入一个数n，返回1+2+3+...+n。
输入两个数m，n(m<n)，返回m*(m+1)*...*n。

数组也可以做方法的参数和返回值。例：把一组整数反转，输出

输入数组x和标准y，统计出x中大于y的数所占比例。

编写两个方法，分别输入和输出一维整形数组[形如read_array(5)和write_array(x)]。

（*为c#专用，下同）
交换（值、数组、数组的值、*引用类型）

{//C#专用

　　//*引用类型代码：

static void swap(ref int x,ref int y)
        {
            int z;
            z = x;
            x = y;
            y = z;
        }
        static void Main(string[] args)
        {
            int a = 100, b = 200;
            swap(ref a, ref b);
            Console.WriteLine(a);
            Console.WriteLine(b);
            Console.ReadKey();
        }

　　内存状态：

}
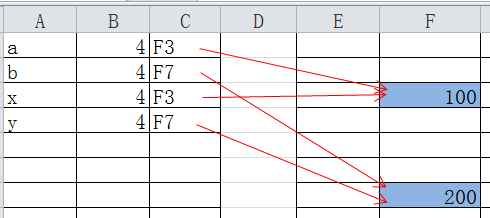
返回多值(字符串、数组、*out、*元组)

out之弃元。

练习，编写方法并调用：

1、求两个整数相除的余数和商。

2、求某半径圆的周长和面积。

最大值3（嵌套调用）
递归：
　　自然数累加（java例5-5）
　　统计入党申请书（见例程士兵报数）

　　java代码：

static int hm(int[] x,int n)
	{
		int c=0;
		if(n>0)
		{
			c=hm(x,n-1);
			if(x[n]==0)
			{
				return c;
			}
			else
			{
				return c+1;
			}
		}
		else
		{
			if(x[n]==0)
			{
				return 0;
			}
			else
			{
				return 1;
			}
		}
	}
	public static void main(String args[])
	{
		int[] a= {0,1,1,0,1,0,1,1,0};
		int count;
		count=hm(a,a.length-1);
		System.out.println(count);
	}

　　c#代码：

private void button1_Click(object sender, EventArgs e)
        {
            int[] a = { 1, 0, 1, 1, 1, 1, 0, 1 };
            label1.Text = "";
            baoshu(a,7);
        }

        int baoshu(int[] a,int y)
        {
            int hear;
            if (y > 0)
            {
                do
                {
                    y--;
                } while (a[y] != 1);
                hear = baoshu(a,y);
                label1.Text += "," + (hear + 1).ToString();
                return hear + 1;
            }
            else
            {
                label1.Text = "1";
                return 1;
            }
        }

　　

　　按顺序逐个输出整数的各位（见例程）

　　　　java代码：

public static void main(String[] args) {
		// TODO Auto-generated method stub
		int a = 17765824;
        String msg=getBit(a);
        System.out.println(msg);
	}
	
	static String getBit(int x)
    {
        String t_s;
        if (x > 9)
        {
            t_s = getBit(x / 10);
            t_s +=","+(x % 10);
        }
        else
        {
            t_s = x+"";
        }
        return t_s;
    }

　　　　c#代码：

        private void button1_Click(object sender, EventArgs e)
        {
            int a = 17765824;
            string msg=getBit(a);
            label1.Text = msg;
        }

        string getBit(int x)
        {
            string t_s;
            if (x > 9)
            {
                t_s = getBit(x / 10);
                t_s +=","+(x % 10).ToString();
            }
            else
            {
                t_s = x.ToString();
            }
            return t_s;
        }

　　

输出斐波拉契数列

思路1，写个递归方法，有一个参数设置是否打印第1至第x-1个数列值。

C#代码:

static void Main(string[] args)
        {
            fblq(10, true);
        }
        static int fblq(int x,bool p)
        {
            int y;
            if (x > 2)
            {
                y=fblq(x - 2,x==3&&p?true:false/*要求打印3的时候，则构成3的1和2都要打印，否则会缺一个1*/) + fblq(x - 1,p?true:false);
            }
            else if(x==2)
            {
                y = 1;
            }
            else
            {
                y = 1;
            }
            if(p)
            {
                Console.Write($"{y}	");
            }
            return y;
        }

思路2：把计算和打印分开

Java代码：

public static void main(String[] args)
    {
        // TODO Auto-generated method stub
        p(10);
    }
    public static int js(int x)
    {
        if(x>2)
        {
            return js(x-2)+js(x-1);
        }
        else
        {
            return 1;
        }
    }
    public static void p(int x)
    {
        if(x>2)
        {
            p(x-1);
            System.out.print("	"+js(x));
        }
        else
        {
            System.out.print("1	1");
        }
    }

----------------------------------

思考题(题目说明引自百度百科)：

汉诺塔：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

八皇后：八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。 高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。计算机发明后，有多种计算机语言可以解决此问题。