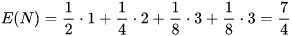0 前言
上"多媒体通信"课，老师讲到了信息论中的一些概念，看到交叉熵，想到这个概念经常用在机器学习中的损失函数中。
这部分知识算是机器学习的先备知识，所以查资料加深一下理解。
1 信息熵的抽象定义
熵的概念最早由统计热力学引入。
信息熵是由信息论之父香农提出来的，它用于随机变量的不确定性度量，先上信息熵的公式。
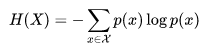
信息是用来减少随机不确定性的东西（即不确定性的减少）。
我们可以用log ( 1/P )来衡量不确定性。P是一件事情发生的概率，概率越大，不确定性越小。
可以看到信息熵的公式，其实就是log ( 1/P )的期望，就是不确定性的期望，它代表了一个系统的不确定性，信息熵越大，不确定性越大。
注意这个公式有个默认前提，就是X分布下的随机变量x彼此之间相互独立。还有log的底默认为2，实际上底是多少都可以，但是在信息论中我们经常讨论的是二进制和比特，所以用2。
信息熵在联合概率分布的自然推广，就得到了联合熵
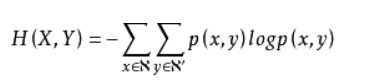
当X, Y相互独立时，H(X, Y) = H(X) + H(Y)
当X和Y不独立时，可以用 I(X, Y) = H(X) + H(Y) - H(X, Y) 衡量两个分布的相关性，这个定义比较少用到。
2 信息熵的实例解释
举个例子说明信息熵的作用。
例子是知乎上看来的，我觉得讲的挺好的。
比如赌马比赛，有4匹马{ A, B, C, D}，获胜概率分别为{ 1/2, 1/4, 1/8, 1/8 }，将哪一匹马获胜视为随机变量X属于 { A, B, C, D } 。
假定我们需要用尽可能少的二元问题来确定随机变量 X 的取值。
例如，问题1：A获胜了吗？ 问题2：B获胜了吗？ 问题3：C获胜了吗？
最后我们可以通过最多3个二元问题，来确定取值。
如果X = A，那么需要问1次（问题1：是不是A？），概率为1/2
如果X = B，那么需要问2次（问题1：是不是A？问题2：是不是B？），概率为1/4
如果X = C，那么需要问3次（问题1，问题2，问题3），概率为1/8
如果X = D，那么需要问3次（问题1，问题2，问题3），概率为1/8
那么为确定X取值的二元问题的数量为
回到信息熵的定义，会发现通过之前的信息熵公式，神奇地得到了：
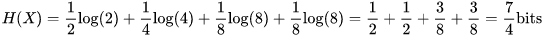
在二进制计算机中，一个比特为0或1，其实就代表了一个二元问题的回答。也就是说，在计算机中，我们给哪一匹马夺冠这个事件进行编码，所需要的平均码长为1.75个比特。
很显然，为了尽可能减少码长，我们要给发生概率
较大的事件，分配较短的码长
。这个问题深入讨论，可以得出霍夫曼编码的概念。
霍夫曼编码就是利用了这种大概率事件分配短码的思想，而且可以证明这种编码方式是最优的。我们可以证明上述现象：
- 为了获得信息熵为
的随机变量
的一个样本，平均需要抛掷均匀硬币（或二元问题）
- 信息熵是数据压缩的一个临界值（参考码长部分的案例）
所以，信息熵H(X)可以看做，对X中的样本进行编码所需要的编码长度的期望值。
3 交叉熵和KL散度
上一节说了信息熵H(X)可以看做，对X中的样本进行编码所需要的编码长度的期望值。
这里可以引申出交叉熵的理解，现在有两个分布，真实分布p和非真实分布q，我们的样本来自真实分布p。
按照真实分布p来编码样本所需的编码长度的期望为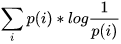
，这就是上面说的信息熵H( p )
按照不真实分布q来编码样本所需的编码长度的期望为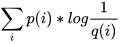
，这就是所谓的交叉熵H( p,q )
这里引申出KL散度D(p||q) = H(p,q) - H(p) =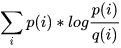 
，也叫做相对熵，它表示两个分布的差异，差异越大，相对熵越大。
机器学习中，我们用非真实分布q去预测真实分布p，因为真实分布p是固定的，D(p||q) = H(p,q) - H(p) 中 H(p) 固定，也就是说交叉熵H(p,q)越大，相对熵D(p||q)越大，两个分布的差异越大。
所以交叉熵用来做损失函数就是这个道理，它衡量了真实分布和预测分布的差异性。
4 另外
哈夫曼编码和上面猜马例子的思想是一致的，使用概率和获胜概率对应，二进制码长和二元问题的数量相对应，最后算出来的平均码长和平均使用的二元问题数量相对应。
香农也证明了哈夫曼这样的编码是最佳编码（平均码长为能达到的最小的极限）。
从编码的角度，可以这样简单总结，信息熵是最优编码（最短的平均码长），交叉熵是非最优编码（大于最短的平均码长），KL散度是两者的差异（距离最优编码的差距）。
5 Reference:
信息熵是什么，韩迪的回答：https://www.zhihu.com/question/22178202
如何通俗的解释交叉熵于相对熵，最高赞匿名用户的回答和张一山的回答：https://www.zhihu.com/question/41252833
转载：https://www.cnblogs.com/liaohuiqiang/p/7673681.html