【LeetCode】142. Linked List Cycle II

Difficulty:medium

 More:【目录】LeetCode Java实现

Description

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

Note: Do not modify the linked list.

Follow up:
Can you solve it without using extra space?

Intuition

1) find out whether there is a cycle, refer to141. Linked List Cycle

2) if there is a cycle, we can get the meetingNode, meanwhile we use a pointer named entry to point to the head Node.

3) let the meetingNode and entry move one step at a time, where they meet is where the cycle begins.

why will they meet at the beginning of the cycle? here is the proof:

　　1. define L1 as the distance between the head node and entry node;

　　2.defined L2 as the distance between the entry node and meeting node;

　　3.defined C as the length of the cycle

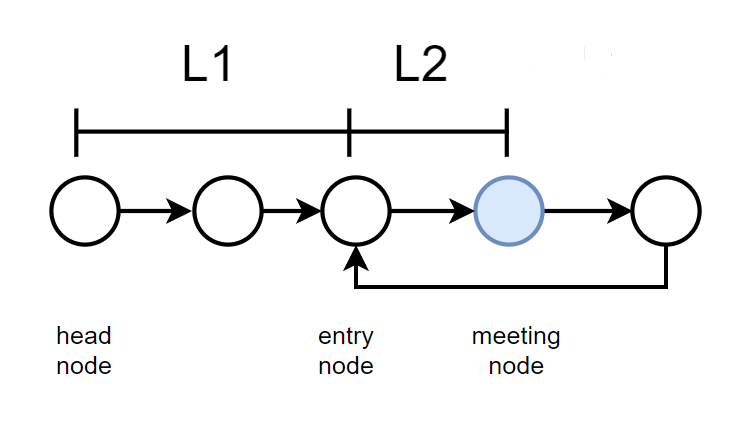
　　We can know that:

　　 the distance of slow node=L1+L2; while the distance of fast node=L1+L2+n*C

　　because of the speed, we have :

　　2*(L1+L2)=L1+L2+n*C => L1=n*C-L2 => L1=(n-1)C+(C-L2)

　　it means that: the distance between the head node and entry node equals the distance between the meeting node and entry node;

Solution

    public ListNode detectCycle(ListNode head) {
        if(head==null)
            return null;
        ListNode fast=head;
        ListNode slow=head;
        ListNode entry=head;
        while(fast.next!=null && fast.next.next!=null){
            fast=fast.next.next;
            slow=slow.next;
            if(fast==slow){
                while(entry!=slow){
                    entry=entry.next;
                    slow=slow.next;
                }
                return entry;
            }
        }
        return null;
    }

　　

Complexity

Time complexity : O(n)

Space complexity : O(1)

 

What I've learned

1. How to prove the distance relation.

 More:【目录】LeetCode Java实现